目录

回归分析

一元线性回归

操作方法

结果分析

结果报告

多元线性回归

操作方法

1. 分析>回归>线性

2. 分类

2.1 进入

结果分析

结果报告

2.2 逐步

结果分析

结果报告

2.3 层次回归

结果分析

---

相关分析用于检验变量间的关系，但仅仅只能确定变量之间是否存在关系，而不能确定这一关系的方向性，例如X与Y之间存在显著正相关关系，但我们无法知道是X水平越高，Y水平随之越高，还是Y水平越高，X水平随之越高。如果想确定变量间关系的方向性，则需用到回归分析（Regression）分析。

回归分析

当因变量为连续变量时，根据自变量的个数，回归分析可分为：

• 一元线性回归（简单直线回归）

• 多元线性回归（复回归分析）

一元线性回归

• 一元线性回归中只涉及到两个变量，一个自变量一个因变量。

• Y = a + bX（Y为效标变量、反应变量；X为预测变量、解释变量）

操作方法

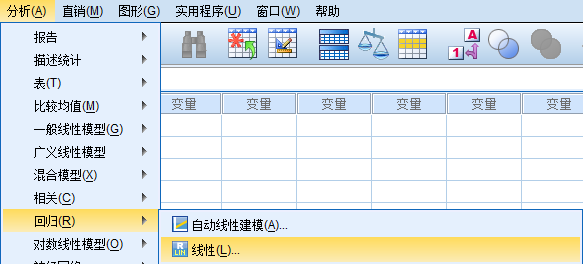
1. 分析>回归>线性

2. 将自变量和因变量添加到对应栏中

3. 点击“统计量”，在弹出的界面中，根据需要勾选

结果分析

1. 描述性统计量和相关性

2. 输入/移去的变量和模型汇总

• 相关系数R

• 决定系数R2：解释率，即因变量的变化有多少是自变量变化引起的

3. Anova

• 回归方程显著性检验，检验整体的自变量对因变量的影响，即回归模型整体解释变异量是否达到了显著水平，Sig < 0.05，说明回归方程显著/有效。

4. 系数

• 非标准化系数、标准化系数、回归系数显著性检验结果

• 回归方程 标准化：Y = 0.555X 非标准化：Y = 0.791 + 0.690X

• 一元线性回归中，回归方程显著，则X的系数t值显著

结果报告

线性回归分析结果显示，X与Y存在显著的线性关系，X可以解释Y的30.9%的变异性，回归方程为Y = 0.791 + 0.690X，是显著的（F = 528.732, P < 0.001）。即可以用X预测Y。

---

多元线性回归

多元线性回归中涉及到多个变量，其中包含一个因变量和多个自变量。

Y = a + bX1 + cX2（Y为因变量、效标变量、反应变量；X为自变量、预测变量、解释变量）

操作方法

1. 分析>回归>线性

2. 分类

根据自变量进入回归方程的方式，可分为以下几种：

2.1 进入

使用强迫进入变量法时，所有自变量被同时纳入回归方程。

结果分析

1. 描述性统计和相关分析

2. 纳入自变量及方法

3. 模型汇总

4. 回归系数

5. 共线性诊断

• 共线性是指回归模型中的某些或者全部自变量存在高度或者完全线性关系的现象。这是回归模型不允许的，为了避免自变量之间的共线性问题，需要进行诊断。

• 诊断方法一：多元共线性的常用指标为容忍度（允差/容差/TOL值）、方差膨胀因素（VIF）、条件指标（CI值）以及特征值（Eigenvalue）。在回归模型中，如果容忍度小于0.01，VIF值大于10，CI值大于30，特征值小于0.01，则说明自变量间存在共线性问题。

• 诊断方法二：如果回归模型中自变量间存在很高的相关，则说明变量间可能存在共线性问题，可以根据以往研究及理论，挑选一个比较重要的自变量纳入回归方程。

• 较为理想情况是自变量间呈低度相关，自变量和因变量间呈高度相关。

结果报告

多元线性回归分析结果显示，X1、X2、X3、X4的多元相关系数为0.660，决定系数为0.436，表示所有自变量共解释因变量的43.6%的变异量。建立回归方程Y = 0.173X1 + 0.221X2 + 0.073X3 + 0.397X4（F = 220.585, p < 0.001），说明X1、X2、X3、X4可以正向预测Y。

2.2 逐步

采用逐步进入变量法，可将不显著的变量排除在外，建立最佳的回归模型。

结果分析

1. 描述性统计和相关分析

2. 纳入/移去的变量

3. 模型汇总

4. ANOVA

5. 回归系数

6. 共线性诊断

结果报告

多元线性回归分析结果显示，X1、X2、X3、X4对因变量有显著的预测力，可解释因变量43.6%的变异量，建立回归方程为：Y = 0.397X4 + 0.221X2 + 0.173X1 + 0.073X3（F = 220.585, p < 0.001）。从每个变量的预测力高低来看，X4、X2、X1、X3分别能够解释34.1%、6.5%、2.6%、0.4%的变异量。

2.3 层次回归

采用层次回归，可以控制协变量的影响。 例如，我们想要控制X1和X2，研究X3和X4对Y的影响。

结果分析

1. 描述性统计和相关分析

2. 输入/移去的变量

3. 模型汇总

4. 回归系数

5. 共线性诊断

---

希望上述介绍可以帮助到你！也欢迎大家在评论区多多交流分享。

你的关注/点赞 /收藏★/分享，是最大的支持！