一、Tensor 之间的运算规则

• 相同大小 Tensor 之间的任何算术运算都会将运算应用到元素级
• 不同大小 Tensor(要求dimension 0 必须相同) 之间的运算叫做广播(broadcasting)
• Tensor 与 Scalar(0维 tensor) 间的算术运算会将那个标量值传播到各个元素
• Note： TensorFLow 在进行数学运算时，一定要求各个 Tensor 数据类型一致

---

二、常用操作符和基本数学函数

大多数运算符都进行了重载操作，使我们可以快速使用 (+ - * /) 等，但是有一点不好的是使用重载操作符后就不能为每个操作命名了。

# 算术操作符：+ - * / % 
tf.add(x, y, name=None)        # 加法(支持 broadcasting)
tf.subtract(x, y, name=None)   # 减法
tf.multiply(x, y, name=None)   # 乘法
tf.divide(x, y, name=None)     # 浮点除法, 返回浮点数(python3 除法)
tf.mod(x, y, name=None)        # 取余


# 幂指对数操作符：^ ^2 ^0.5 e^ ln 
tf.pow(x, y, name=None)        # 幂次方
tf.square(x, name=None)        # 平方
tf.sqrt(x, name=None)          # 开根号，必须传入浮点数或复数
tf.exp(x, name=None)           # 计算 e 的次方
tf.log(x, name=None)           # 以 e 为底，必须传入浮点数或复数


# 取符号、负、倒数、绝对值、近似、两数中较大/小的
tf.negative(x, name=None)      # 取负(y = -x).
tf.sign(x, name=None)          # 返回 x 的符号
tf.reciprocal(x, name=None)    # 取倒数
tf.abs(x, name=None)           # 求绝对值
tf.round(x, name=None)         # 四舍五入
tf.ceil(x, name=None)          # 向上取整
tf.floor(x, name=None)         # 向下取整
tf.rint(x, name=None)          # 取最接近的整数 
tf.maximum(x, y, name=None)    # 返回两tensor中的最大值 (x > y ? x : y)
tf.minimum(x, y, name=None)    # 返回两tensor中的最小值 (x < y ? x : y)


# 三角函数和反三角函数
tf.cos(x, name=None)    
tf.sin(x, name=None)    
tf.tan(x, name=None)    
tf.acos(x, name=None)
tf.asin(x, name=None)
tf.atan(x, name=None)   


# 其它
tf.div(x, y, name=None)  # python 2.7 除法, x/y-->int or x/float(y)-->float
tf.truediv(x, y, name=None) # python 3 除法, x/y-->float
tf.floordiv(x, y, name=None)  # python 3 除法, x//y-->int
tf.realdiv(x, y, name=None)
tf.truncatediv(x, y, name=None)
tf.floor_div(x, y, name=None)
tf.truncatemod(x, y, name=None)
tf.floormod(x, y, name=None)
tf.cross(x, y, name=None)
tf.add_n(inputs, name=None)  # inputs: A list of Tensor objects, each with same shape and type
tf.squared_difference(x, y, name=None) 
 
 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50

---

三、矩阵数学函数

# 矩阵乘法(tensors of rank >= 2)
tf.matmul(a, b, transpose_a=False, transpose_b=False,    adjoint_a=False, adjoint_b=False, a_is_sparse=False, b_is_sparse=False, name=None)


# 转置，可以通过指定 perm=[1, 0] 来进行轴变换
tf.transpose(a, perm=None, name='transpose')


# 在张量 a 的最后两个维度上进行转置
tf.matrix_transpose(a, name='matrix_transpose')
# Matrix with two batch dimensions, x.shape is [1, 2, 3, 4]
# tf.matrix_transpose(x) is shape [1, 2, 4, 3]


# 求矩阵的迹
tf.trace(x, name=None)


# 计算方阵行列式的值
tf.matrix_determinant(input, name=None)


# 求解可逆方阵的逆，input 必须为浮点型或复数
tf.matrix_inverse(input, adjoint=None, name=None)


# 奇异值分解
tf.svd(tensor, full_matrices=False, compute_uv=True, name=None)


# QR 分解
tf.qr(input, full_matrices=None, name=None)


# 求张量的范数(默认2)
tf.norm(tensor, ord='euclidean', axis=None, keep_dims=False, name=None)



# 构建一个单位矩阵, 或者 batch 个矩阵，batch_shape 以 list 的形式传入
tf.eye(num_rows, num_columns=None, batch_shape=None, dtype=tf.float32, name=None)
# Construct one identity matrix.
tf.eye(2)
==> [[1., 0.],
     [0., 1.]]

# Construct a batch of 3 identity matricies, each 2 x 2.
# batch_identity[i, :, :] is a 2 x 2 identity matrix, i = 0, 1, 2.
batch_identity = tf.eye(2, batch_shape=[3])

# Construct one 2 x 3 "identity" matrix
tf.eye(2, num_columns=3)
==> [[ 1.,  0.,  0.],
     [ 0.,  1.,  0.]]


# 构建一个对角矩阵，rank = 2*rank(diagonal)
tf.diag(diagonal, name=None)
# 'diagonal' is [1, 2, 3, 4]
tf.diag(diagonal) ==> [[1, 0, 0, 0]
                       [0, 2, 0, 0]
                       [0, 0, 3, 0]
                       [0, 0, 0, 4]]



# 其它
tf.diag_part
tf.matrix_diag
tf.matrix_diag_part
tf.matrix_band_part
tf.matrix_set_diag
tf.cholesky
tf.cholesky_solve
tf.matrix_solve
tf.matrix_triangular_solve
tf.matrix_solve_ls
tf.self_adjoint_eig
tf.self_adjoint_eigvals
 
 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79

---

四、Reduction：reduce various dimensions of a tensor

# 计算输入 tensor 所有元素的和，或者计算指定的轴所有元素的和
tf.reduce_sum(input_tensor, axis=None, keep_dims=False, name=None)
# 'x' is [[1, 1, 1]
#         [1, 1, 1]]
tf.reduce_sum(x) ==> 6
tf.reduce_sum(x, 0) ==> [2, 2, 2]
tf.reduce_sum(x, 1) ==> [3, 3]
tf.reduce_sum(x, 1, keep_dims=True) ==> [[3], [3]]  # 维度不缩减
tf.reduce_sum(x, [0, 1]) ==> 6


# 计算输入 tensor 所有元素的均值/最大值/最小值/积/逻辑与/或
# 或者计算指定的轴所有元素的均值/最大值/最小值/积/逻辑与/或(just like reduce_sum)
tf.reduce_mean(input_tensor, axis=None, keep_dims=False, name=None)
tf.reduce_max(input_tensor, axis=None, keep_dims=False, name=None)
tf.reduce_min(input_tensor, axis=None, keep_dims=False, name=None)
tf.reduce_prod(input_tensor, axis=None, keep_dims=False, name=None)
tf.reduce_all(input_tensor, axis=None, keep_dims=False, name=None)  # 全部满足条件
tf.reduce_any(input_tensor, axis=None, keep_dims=False, name=None) #至少有一个满足条件


-------------------------------------------
# 分界线以上和 Numpy 中相应的用法完全一致
-------------------------------------------



# inputs 为一 list, 计算 list 中所有元素的累计和，
# tf.add(x, y， name=None)只能计算两个元素的和，此函数相当于扩展了其功能
tf.accumulate_n(inputs, shape=None, tensor_dtype=None, name=None)


# Computes log(sum(exp(elements across dimensions of a tensor)))
tf.reduce_logsumexp(input_tensor, axis=None, keep_dims=False, name=None)


# Computes number of nonzero elements across dimensions of a tensor
tf.count_nonzero(input_tensor, axis=None, keep_dims=False, name=None)
 
 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38

---

五、Scan：perform scans (running totals) across one axis of a tensor

# Compute the cumulative sum of the tensor x along axis
tf.cumsum(x, axis=0, exclusive=False, reverse=False, name=None)
# Eg:
tf.cumsum([a, b, c])  # => [a, a + b, a + b + c]
tf.cumsum([a, b, c], exclusive=True)  # => [0, a, a + b]
tf.cumsum([a, b, c], reverse=True)  # => [a + b + c, b + c, c]
tf.cumsum([a, b, c], exclusive=True, reverse=True)  # => [b + c, c, 0]


# Compute the cumulative product of the tensor x along axis
tf.cumprod(x, axis=0, exclusive=False, reverse=False, name=None)
 
 
1
2
3
4
5
6
7
8
9
10
11

---

六、Segmentation

沿着第一维(x 轴)根据 segment_ids(list)分割好相应的数据后再进行操作

# Computes the sum/mean/max/min/prod along segments of a tensor
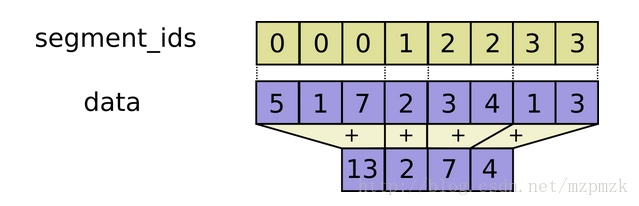
tf.segment_sum(data, segment_ids, name=None)
# Eg:
m = tf.constant([5,1,7,2,3,4,1,3])
s_id = [0,0,0,1,2,2,3,3]
s.run(tf.segment_sum(m, segment_ids=s_id))
>array([13,  2,  7,  4], dtype=int32)

tf.segment_mean(data, segment_ids, name=None)
tf.segment_max(data, segment_ids, name=None)
tf.segment_min(data, segment_ids, name=None)
tf.segment_prod(data, segment_ids, name=None)


# 其它
tf.unsorted_segment_sum
tf.sparse_segment_sum
tf.sparse_segment_mean
tf.sparse_segment_sqrt_n
 
 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

---

七、 序列比较与索引提取

# 比较两个 list 或者 string 的不同，并返回不同的值和索引
tf.setdiff1d(x, y, index_dtype=tf.int32, name=None)


# 返回 x 中的唯一值所组成的tensor 和原 tensor 中元素在现 tensor 中的索引
tf.unique(x, out_idx=None, name=None)


# x if condition else y, condition 为 bool 类型的，可用tf.equal()等来表示
# x 和 y 的形状和数据类型必须一致
tf.where(condition, x=None, y=None, name=None)


# 返回沿着坐标轴方向的最大/最小值的索引
tf.argmax(input, axis=None, name=None, output_type=tf.int64)
tf.argmin(input, axis=None, name=None, output_type=tf.int64)


# x 的值当作 y 的索引，range(len(x)) 索引当作 y 的值
# y[x[i]] = i for i in [0, 1, ..., len(x) - 1]
tf.invert_permutation(x, name=None)


# 其它
tf.edit_distance
 
 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

---

八、参考资料

http://blog.csdn.net/mzpmzk/article/details/77337851