函数定义

tf.nn.conv2d(input, filter, strides, padding, use_cudnn_on_gpu=None, data_format=None, name=None)

功能：在给定4-D 输入和fliters的情况下，计算二维卷积。

input的shape: [batch, in_height, in_width, in_channels]
filter的shape: [filter_height, filter_width, in_channels, out_channels]

计算过程如下：
（１）展平filter成如下2-D matrix，其shape: [filter_height * filter_width * in_channels, output_channels]
（２）从input tensor中提取patches构成一个virtual tensor, 其shape: [batch, out_height, out_width, filter_height * filter_width * in_channels]
（３）对于每一个patch,　右乘上（１）中的filter matrix。即[batch, out_height, out_width, filter_height * filter_width * in_channels]　x [filter_height * filter_width * in_channels, output_channels]，其结果的shape就是[batch, out_height, out_width, output_channels]。

【注：必须有 strides[0] = strides[3] = 1】。绝大多数情况下，水平的stride和竖直的stride一样，即strides = [1, stride, stride, 1]。

输出结果的shape计算：
‘SAME’ 类型的padding,其输出的height和width计算如下：
out_height = ceil(float(in_height) / float(strides[1])) ceil：向上取整
out_width = ceil(float(in_width) / float(strides[2]))

‘VALID’类型的padding, 其输出的height和width计算如下：
out_height = ceil(float(in_height – filter_height + 1) / float(strides[1]))
out_width = ceil(float(in_width – filter_width + 1) / float(strides[2]))

【注：tensorflow中的卷积，严格上来说是cross-correlation，而不是卷积。因为在计算的过程中，没有对filter进行翻转，而严格的卷积计算是需要对filter进行翻转的！！！】

代码验证

tensorflow中的tf.nn.conv2d函数，实际上相当于用filter，以一定的步长stride在image上进行滑动，计算重叠部分的内积和，即为卷积结果。下面从定义出发对tf.nn.conv2d函数的功能进行验证：

# -*- coding: utf-8 -*-

from __future__ import division
import tensorflow as tf
import numpy as np
import math
import pandas as pd

input_arr = np.zeros((12, 15), dtype=np.float32)
number = 0
for row_idx in range(input_arr.shape[0]):
    for col_idx in range(input_arr.shape[1]):
        input_arr[row_idx][col_idx] = number
        number += 1

number = 6
w_arr = np.zeros((2, 3), dtype=np.float32)
for row_idx in range(w_arr.shape[0]):
    for col_idx in range(w_arr.shape[1]):
        w_arr[row_idx][col_idx] = number
        number -= 1

stride = [1, 1, 1, 1]

# 从卷积的定义【实际上不是卷积，而是cross-correlation】进行计算验证---对VALID类型卷积进行验证
res_shape_0 = int(math.ceil((input_arr.shape[0] - w_arr.shape[0] + 1) / stride[1]))
res_shape_1 = int(math.ceil((input_arr.shape[1] - w_arr.shape[1] + 1) / stride[2]))
validation_res = np.zeros(shape=(res_shape_0, res_shape_1), dtype=np.float32)

for row_idx in range(validation_res.shape[0]):
    for col_idx in range(validation_res.shape[1]):
        patch = input_arr[row_idx:row_idx+w_arr.shape[0], col_idx:col_idx+w_arr.shape[1]]
        # 这里的　*　实际上代表的是点积，即对应元素位置相乘
        res = np.sum(patch * w_arr)
        validation_res[row_idx][col_idx] = res

print('result of convolution from its definition: validation_res')
print validation_res
pd.DataFrame(validation_res).to_csv('Results/validation_res.csv', index=False, header=False)

input_arr = np.reshape(input_arr, [1, input_arr.shape[0], input_arr.shape[1], 1])
w_arr = np.reshape(w_arr, [w_arr.shape[0], w_arr.shape[1], 1, 1])

# 相当于要输入的图片，shape: [1, 12, 15, 1]
net_in = tf.constant(value=input_arr, dtype=tf.float32)

# 相当于filter, shape: [2, 3, 1, 1]
W = tf.constant(value=w_arr, dtype=tf.float32)

# tensorflow卷积的计算结果：
# valid卷积结果, shape: [1, 11, 13, 1]
result_conv_valid = tf.nn.conv2d(net_in, W, stride, 'VALID', True)

# same卷积结果, shape: [1, 12, 15, 1]
result_conv_same = tf.nn.conv2d(net_in, W, stride, 'SAME', True)

sess = tf.Session()
sess.run(tf.global_variables_initializer())

valid_conv_res = sess.run(result_conv_valid)
same_conv_res = sess.run(result_conv_same)
sess.close()

print valid_conv_res.shape
valid_conv_res = np.reshape(valid_conv_res, [valid_conv_res.shape[1], valid_conv_res.shape[2]])
same_conv_res = np.reshape(same_conv_res, [same_conv_res.shape[1], same_conv_res.shape[2]])
print('tensorflow conv res: valid_conv_res')
print valid_conv_res
pd.DataFrame(valid_conv_res).to_csv('Results/conv_res.csv', index=False, header=False)
pd.DataFrame(same_conv_res).to_csv('Results/result_conv_same.csv', index=False, header=False)

上面代码，只针对valid卷积类型进行了验证，对same的卷积类型没有验证【same类型的卷积，其padding方式还不懂，求懂的高手指教】。计算结果保存到了相应的csv文件中。
（１）Tensorflow valid类型卷积计算结果：

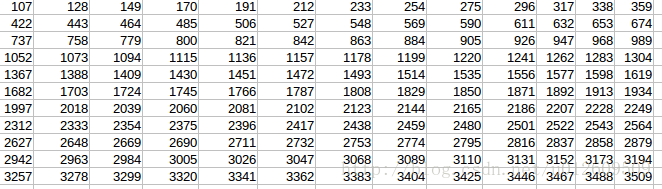
（２）Tensorflow same类型卷积计算结果：

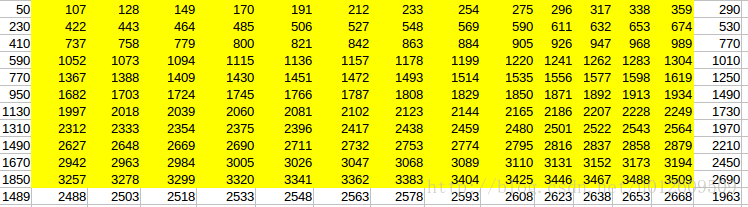
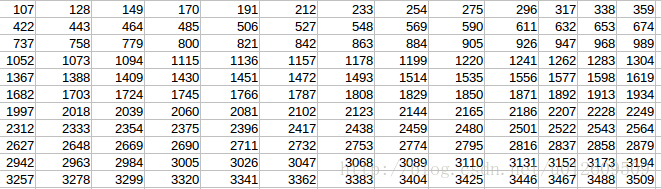
（３）从卷积定义出发，valid类型卷积计算结果：

可以看出，其验证结果是正确的。并且same和valid的卷积结果，除边缘部分外，其余的值都是一样的。