前面 有篇博文讲了多层感知器，也就是一般的前馈神经网络，文章里使用 CIFAR10 数据集得到的测试准确率是 46.98%。今天我们使用更适合处理图像的卷积神经网络来处理相同的数据集 - CIFAR10，来看下准确率能达到多少。

本文代码基于 TensorFlow 的官方文档 做了些许修改，完整代码及结果图片可从 这里 下载。

这篇 文章是对本文的一个升级，增加了 TensorBoard 的实现，可以在浏览器中查看可视化结果，包括准确率、损失、计算图、训练时间和内存信息等。

---

更新

这里我会列出对本文的更新。

• 2017年3月17日：增加实现 TensorBoard 的文章的链接。

---

原理

关于卷积神经网络（Convolutional Neural Network，以下简称 CNN）网上有很多优秀的教程，我在这里也不再重复造轮子，强烈推荐 斯坦福的CS321n，讲的很全面。

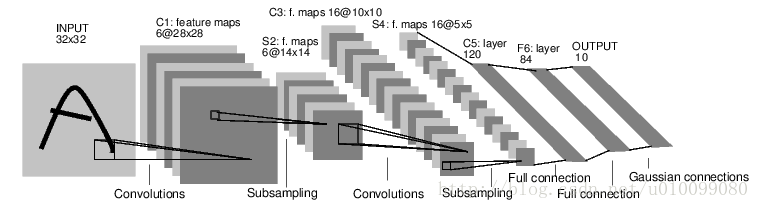
还是和以前一样，我在这里简单说下 CNN 的原理。首先来看下一个典型的 CNN - LeNet5 的结构图，

这个 CNN 是 Yann LeCun 在 1998 年发表的论文 Gradient-Based Learning Applied to Document Recognition 中所提出的，用于字符识别。如上图，模型输入是一个字符图像，然后对输入进行卷积操作（矩阵点乘求和）得到 C1 卷积层，再进行下采样操作（缩减维度）得到 S2 池化层或者叫下采样层，然后重复一遍刚才的操作，将二维数据 拉平，连着一个多层的普通神金网络，最终得到输出。训练这个模型的方法还是梯度下降法，或者其变种。

---

数据集

数据集仍然采用 CIFAR10，包含 60000 张 32×32 的彩色RGB图像，共有 10 类，每类有 6000 张图像。完整数据集可以从 这里 下载，注意选择 Python 版本，大概是 163 MB。

下载好后解压会看到有 5 个训练文件和 1 个测试文件，还有一个说明文件 batches.meta，这个文件说明了每个数字类别（0-9）具体代表哪些类别。这几个文件都是用 cPickle 打包好的，所以载入数据也要用 cPickle 来载入。注意 Python2 和 Python3 的载入方式稍微有些不同，具体见代码，我使用的是 Python3。

目前在此数据集上做的实验在没有数据增加的情况下最低的错误率是 18%，数据增加的情况下最低的错误率是 11%，都是采用的卷积神经网络（CNN）的结构。

数据集中的图像和分类大致是这样的：

---

代码

由于完整代码较长，这里仅列出关键代码，便于理解整个模型，完整代码可从 这里 下载。

# coding: utf-8

with tf.device('/cpu:0'):

    # 模型参数
    learning_rate = 1e-3
    training_iters = 500
    batch_size = 50
    display_step = 5
    n_features = 3072  # 32*32*3
    n_classes = 10
    n_fc1 = 384
    n_fc2 = 192

    # 构建模型
    x = tf.placeholder(tf.float32, [None, n_features])
    y = tf.placeholder(tf.float32, [None, n_classes])


    w = {
        'conv1': tf.Variable(tf.truncated_normal([5, 5, 3, 64], stddev=5e-2)),
        'conv2': tf.Variable(tf.truncated_normal([5, 5, 64, 64], stddev=0.1)),
        'fc1': tf.Variable(tf.truncated_normal([8*8*64, n_fc1], stddev=0.04)),
        'fc2': tf.Variable(tf.truncated_normal([n_fc1, n_fc2], stddev=0.1)),
        'fc3': tf.Variable(tf.truncated_normal([n_fc2, n_classes], stddev=1/192.0))
    }
    b = {
        'conv1': tf.Variable(tf.constant(0.0, dtype=tf.float32, shape=[64])),
        'conv2': tf.Variable(tf.constant(0.1, dtype=tf.float32, shape=[64])),
        'fc1': tf.Variable(tf.constant(0.1, dtype=tf.float32, shape=[n_fc1])),
        'fc2': tf.Variable(tf.constant(0.1, dtype=tf.float32, shape=[n_fc2])),
        'fc3': tf.Variable(tf.constant(0.0, dtype=tf.float32, shape=[n_classes]))
    }

    x4d = tf.reshape(x, [-1, 32, 32, 3])
    # 卷积层 1
    conv1 = tf.nn.conv2d(x4d, w['conv1'], strides=[1, 1, 1, 1], padding='SAME')
    conv1 = tf.nn.bias_add(conv1, b['conv1'])
    conv1 = tf.nn.relu(conv1)
    # 池化层 1
    pool1 = tf.nn.max_pool(conv1, ksize=[1, 3, 3, 1], strides=[1, 2, 2, 1], padding='SAME')
    # LRN层，Local Response Normalization
    norm1 = tf.nn.lrn(pool1, 4, bias=1.0, alpha=0.001/9.0, beta=0.75)
    # 卷积层 2
    conv2 = tf.nn.conv2d(norm1, w['conv2'], strides=[1, 1, 1, 1], padding='SAME')
    conv2 = tf.nn.bias_add(conv2, b['conv2'])
    conv2 = tf.nn.relu(conv2)
    # LRN层，Local Response Normalization
    norm2 = tf.nn.lrn(conv2, 4, bias=1.0, alpha=0.001/9.0, beta=0.75)
    # 池化层 2
    pool2 = tf.nn.max_pool(norm2, ksize=[1, 3, 3, 1], strides=[1, 2, 2, 1], padding='SAME')
    reshape = tf.reshape(pool2, [-1, 8*8*64])
    dim = reshape.get_shape()[1].value
    fc1 = tf.add(tf.matmul(reshape, w['fc1']), b['fc1'])
    fc1 = tf.nn.relu(fc1)
    # 全连接层 2
    fc2 = tf.add(tf.matmul(fc1, w['fc2']), b['fc2'])
    fc2 = tf.nn.relu(fc2)
    # 全连接层 3, 即分类层
    fc3 = tf.add(tf.matmul(fc2, w['fc3']), b['fc3'])

    # 定义损失
    cost = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(fc3, y))
    optimizer = tf.train.AdamOptimizer(learning_rate=learning_rate).minimize(cost)
    # 评估模型
    correct_pred = tf.equal(tf.argmax(fc3, 1), tf.argmax(y, 1))
    accuracy = tf.reduce_mean(tf.cast(correct_pred, tf.float32))

    init = tf.global_variables_initializer()

with tf.Session() as sess:
    sess.run(init)
    c = []
    total_batch = int(X_train.shape[0] / batch_size)
    for i in range(training_iters):
        avg_cost = 0
        for batch in range(total_batch):
            batch_x = X_train[batch*batch_size : (batch+1)*batch_size, :]
            batch_y = y_train[batch*batch_size : (batch+1)*batch_size, :]
            _, co = sess.run([optimizer, cost], feed_dict={x: batch_x, y: batch_y})
            avg_cost += co

        c.append(avg_cost)
        if (i+1) % display_step == 0:
            print("Iter " + str(i+1) + ", Training Loss= " + "{:.6f}".format(avg_cost))

    print("Optimization Finished!")

    # Test
    test_acc = sess.run(accuracy, feed_dict={x: X_test, y: y_test})
    print("Testing Accuracy:", test_acc)

---

结果

其中的缩写仍然遵照我以前博文的习惯：

• lr：learning rate，学习率
• ti：training iters，训练迭代次数
• bs：batch size，batch大小
• acc：测试准确率

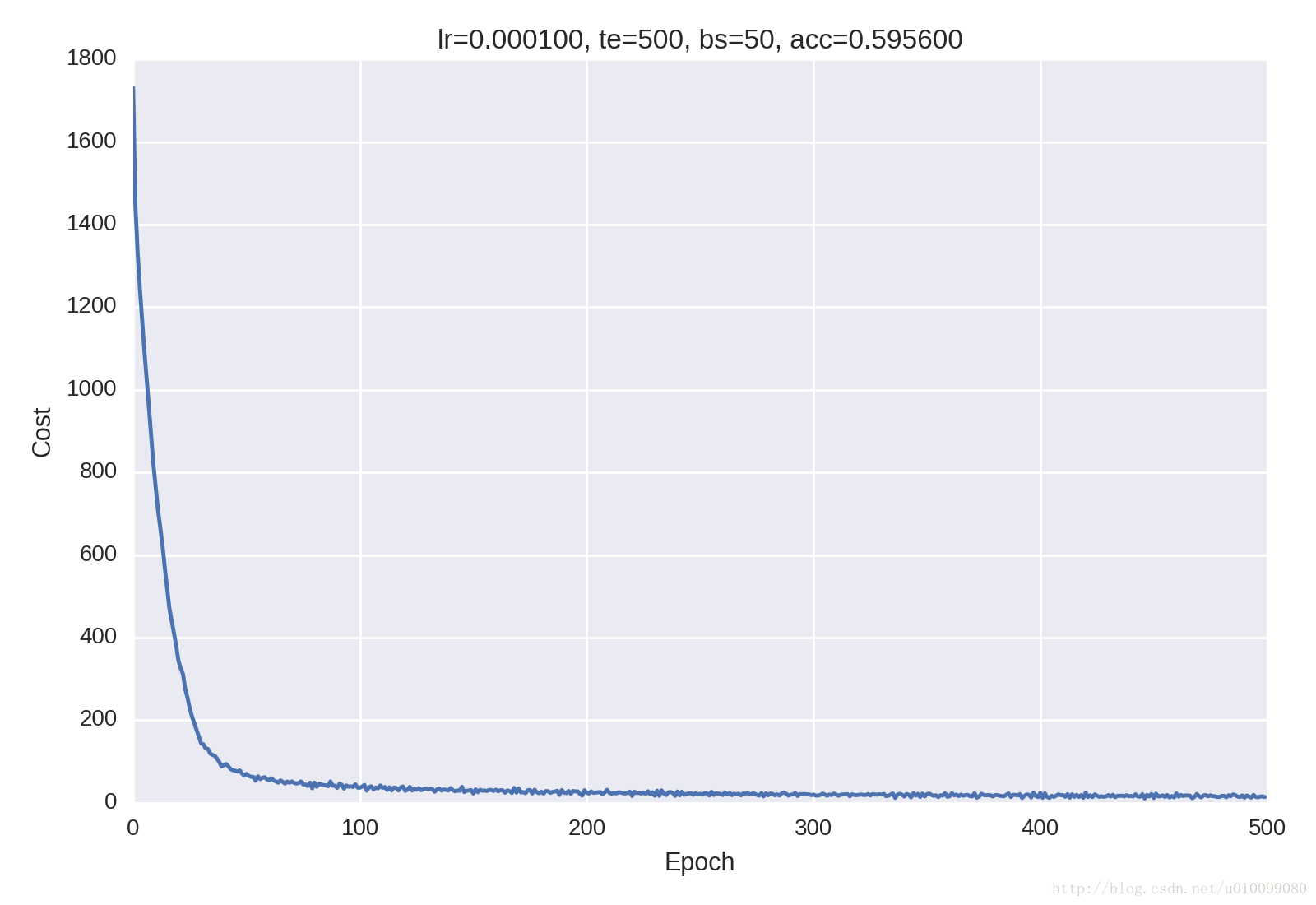
每次结果都会不一样，上图是最好的结果的时候，其他结果图的下载链接和上面一样，测试准确率大约为 60%，其实这个准确率并不高，和 TensorFlow 的官方文档 所得到的 86% 还差一段距离，和官方文档的差距在于我并没有对数据进行更多的预处理，例如图像裁剪到 24×24 的尺寸、标准化、随机左右翻转图像或者随机改变图像亮度和对比度以扩大数据集等等，等有时间再进行进一步的实验，与本次实验进行对比。

在其他条件一样的情况下，本次实验得到的准确率可能并不是最高的，鉴于机器太垃圾，运行一次实验需要两三天，未能进行更多的测试。

---

END