这是TensorFlow文档中的一个例子（参加文献【1】，代码笔者略有改动），可以作为学习TensorFlow的一个实例教程。同时，借由这个例子也可以方便读者理解Softmax，或称多元逻辑回归（ Multinomial Logistic Regression），的基本思想。在学习本文之前，读者应该参考如下两篇文章，以补充必要之基础。

• 从逻辑回归到多元逻辑回归（Multinomial Logistic Regression ）
• TensorFlow简明入门宝典
  

一、关于数据集

作为例子，我们这里要完成的任务是对0~9这十个手写数字进行分类。所使用的数据集为著名的MINST，其中的每一个输入文件都是像下面中的一个这样的一副大小为28x28的图像。

关于这个数据集的更多信息，你还可以参考Yann LeCun的网站（http://yann.lecun.com/exdb/mnist/）。

首先要做的事情当然是引入TensorFlow，并读入数据，因为MNIST这个数据集太有名（几乎是用来做深度学习编程示例的最被频繁使用的一个数据集），TensorFlow中已经将其包含，所以直接用下面的语句就可以将其读入：

import tensorflow as tf
from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets('MNIST_data', one_hot=True)

MNIST 数据集被划分成了3个部分:

• 训练数据 (mnist.train)，包含 55000 个数据点；
• 测试数据（mnist.test)， 包含 10000 个数据点；
• 验证数据（mnist.validation)，包含 5000 个数据点。

每一个 MNIST 数据点都包含两部分：一幅手写数字的图像（称为"x"）以及一个对应的标签（称为"y"）。训练数据集和测试数据集皆是如此。例如，训练数据的图像就是 mnist.train.images，测试数据的标签就是mnist.train.labels。

注意，这里每个输入的图像的都是一个28x28的矩阵（如下图所示），所以也可以看成是28x28=784维的一个向量。

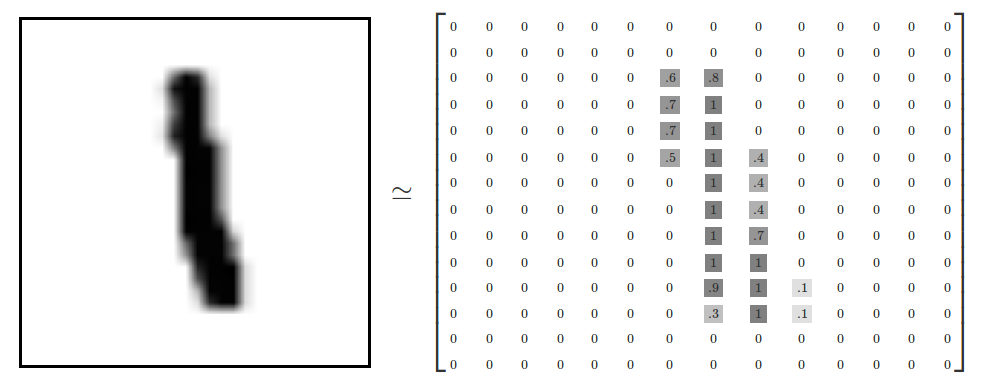
而上面的代码中我们令参数 one_hot = True，则表示，我们需要一个one-hot vector形式的label。例如，对于数字3，它的标签就应该为[0, 0, 0, 1, 0, 0, 0, 0, 0, 0]。

所以 mnist.train.images 是一个张量 （tensor），其shape是 [55000, 784]，如下图所示。张量的概念我们在本文开始给出的推荐阅读内容中介绍过，可以简单理解为“多维数组”。上述张量的第一个维度表示图像在列表中标签，第二个维度则表示（单独一个图像中）每个像素的标签。张量（多维数组）中的每一个值都是介于0到1之间的一个数字，用于表示图像某一点上像素的灰度值。

同时，也可以知道mnist.train.labels 是一个shape为 [55000, 10] 的张量。横轴表示55000个训练数据点（也就是对应图像的下标），纵轴表示该数据点（图像）之标签的one-hot vector向量表示。

二、关于Softmax

Softmax就是二元逻辑回归的推广，亦是最常用的全连接前馈神经网络。如果你了解逻辑回归，那么你可以参考前面推荐的《Multinomial Logistic Regression 》来从逻辑回归的角度理解它。如果你了解感知机模型，那么你也可以参考文献【2】从感知机入手理解它。

对于一个输入的数据点x_i={x₁,x₂,...,x_n}，我们可以仿照线性回归的方法给它找到一组权重W_i 和一个偏置 b 把它映射到因变量空间，线性的映射可以写为

但是我们希望得到的是关于分类判别的一个概率值，所以要加一个softmax函数把上面的线性组合“扭曲”（投影）到新的取值范围内，即（其中y是一个表示各种分类结果可能性的向量）

其中，softmax函数的形式如下

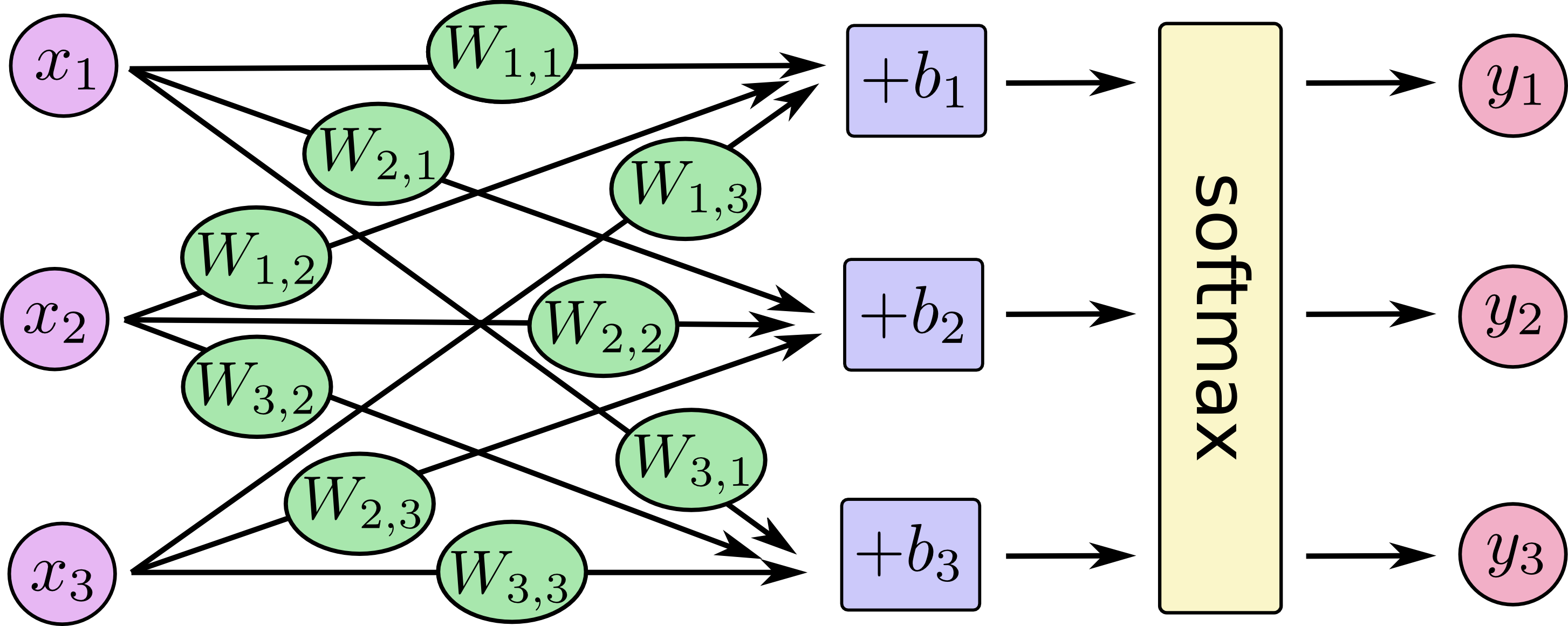
如果你把全连接的前馈神经网络图画出来，那么它的形式如下（假设每个数据点的特征向量维度是3，而且分类结果也只有3种，注意特征向量的维度和分类结果的种类可以不同，例如在我们的MINST例子中，输入图像的向量大小是724，但是分类结果只有10种）：

如果你把所有的方程合在一起写出方程组的形式，则有：

或者也可以用矩阵的形式来表示：

上面的公式相当于 y = softmax(Wx + b)，其实下面我们在编程实现的使用使用的是y = softmax(xW + b)。

三、在TensorFlow中实现

首先用一个占位符来代替 由每个数据点的特征向量组合而成的矩阵，其shape为[None, 784]，其中None表示任意大小（如果你用本例中的训练数据集训练，那么它就是55000）

x = tf.placeholder(tf.float32, [None, 784])

为了先来模型，还得定义一个占位符来储存，训练数据集对应的分类标签：

y_ = tf.placeholder(tf.float32, [None, 10])

然后定义权重矩阵W和偏置向量b，并由此写出y=xW+b的算式：

W = tf.Variable(tf.zeros([784, 10]))
b = tf.Variable(tf.zeros([10]))
y = tf.matmul(x, W) + b

我们使用cross-entropy来作为损失函数，cross-entropy 函数定义为：

在TensorFlow中可以写成下面这样（但实际中我们并不需要自己定义cross-entropy，而是采用后面给出的方法）：

cross_entropy = tf.reduce_mean(-tf.reduce_sum(y_ * tf.log(y), reduction_indices=[1]))

最简单的方法其实是直接调用tf.nn.softmax_cross_entropy_with_logits，即

cross_entropy = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(labels=y_, logits=y))

然后采用梯度下降法来训练模型：

train_step = tf.train.GradientDescentOptimizer(0.5).minimize(cross_entropy)

接下来跟我们之前在《TensorFlow简明入门宝典 》中介绍的情况一样，就可以开始训练模型了，我们迭代1000轮，每次取其中的100个做batch梯度下降：

sess = tf.InteractiveSession()
tf.global_variables_initializer().run()

# Train
for _ in range(1000):
    batch_xs, batch_ys = mnist.train.next_batch(100)
    sess.run(train_step, feed_dict={x: batch_xs, y_: batch_ys})

最后来评估一下训练好的模型效果如何：

# Test trained model
correct_prediction = tf.equal(tf.argmax(y, 1), tf.argmax(y_, 1))
accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))
print(sess.run(accuracy, feed_dict={x: mnist.test.images,
                                      y_: mnist.test.labels}))

在我的测试中准确率在 92%左右。完整的jupyter notebook文件，你可以在文献【3】中获取。

参考文献

【1】https://www.tensorflow.org/get_started/mnist/beginners

【2】Michael Nielsen，http://neuralnetworksanddeeplearning.com/

【3】完全代码下载：https://pan.baidu.com/s/1nu8ZvEL

（本文完）