我们需要评估模型预测值来评估训练的好坏。
模型评估是非常重要的，随后的每个模型都有模型评估方式。使用TensorFlow时，需要把模型评估加入到计算图中，然后在模型训练完后调用模型评估。

在训练模型过程中，模型评估能洞察模型算法，给出提示信息来调试、提高或者改变整个模型。但是在模型训练中并不是总需要模型评估，我们将展示如何在回归算法和分类算法中使用它。

训练模型之后，需要定量评估模型的性能如何。在理想情况下，评估模型需要一个训练数据集和测试数据集，有时甚至需要一个验证数据集。

想评估一个模型时就得使用大批量数据点。如果完成批量训练，我们可以重用模型来预测批量数据点。但是如果要完成随机训练，就不得不创建单独的评估器来处理批量数据点。

分类算法模型基于数值型输入预测分类值，实际目标是1和0的序列。我们需要度量预测值与真实值之间的距离。分类算法模型的损失函数一般不容易解释模型好坏，所以通常情况是看下准确预测分类的结果的百分比。

不管算法模型预测的如何，我们都需要测试算法模型，这点相当重要。在训练数据和测试数据上都进行模型评估，以搞清楚模型是否过拟合。

# TensorFlowm模型评估
#
# This code will implement two models.  The first
#  is a simple regression model, we will show how to
#  call the loss function, MSE during training, and
#  output it after for test and training sets.
#
# The second model will be a simple classification
#  model.  We will also show how to print percent
#  classified correctly during training and after
#  for both the test and training sets.

import matplotlib.pyplot as plt
import numpy as np
import tensorflow as tf
from tensorflow.python.framework import ops
ops.reset_default_graph()

# 创建计算图
sess = tf.Session()

# 回归例子:
# We will create sample data as follows:
# x-data: 100 random samples from a normal ~ N(1, 0.1)
# target: 100 values of the value 10.
# We will fit the model:
# x-data * A = target
# 理论上, A = 10.

# 声明批量大小
batch_size = 25

# 创建数据集
x_vals = np.random.normal(1, 0.1, 100)
y_vals = np.repeat(10., 100)
x_data = tf.placeholder(shape=[None, 1], dtype=tf.float32)
y_target = tf.placeholder(shape=[None, 1], dtype=tf.float32)

# 八二分训练/测试数据 train/test = 80%/20%
train_indices = np.random.choice(len(x_vals), round(len(x_vals)*0.8), replace=False)
test_indices = np.array(list(set(range(len(x_vals))) - set(train_indices)))
x_vals_train = x_vals[train_indices]
x_vals_test = x_vals[test_indices]
y_vals_train = y_vals[train_indices]
y_vals_test = y_vals[test_indices]

# 创建变量 (one model parameter = A)
A = tf.Variable(tf.random_normal(shape=[1,1]))

# 增加操作到计算图
my_output = tf.matmul(x_data, A)

# 增加L2损失函数到计算图
loss = tf.reduce_mean(tf.square(my_output - y_target))

# 创建优化器
my_opt = tf.train.GradientDescentOptimizer(0.02)
train_step = my_opt.minimize(loss)

# 初始化变量
init = tf.global_variables_initializer()
sess.run(init)

# 迭代运行
# 如果在损失函数中使用的模型输出结果经过转换操作，例如，sigmoid_cross_entropy_with_logits（）函数，
# 为了精确计算预测结果，别忘了在模型评估中也要进行转换操作。
for i in range(100):
    rand_index = np.random.choice(len(x_vals_train), size=batch_size)
    rand_x = np.transpose([x_vals_train[rand_index]])
    rand_y = np.transpose([y_vals_train[rand_index]])
    sess.run(train_step, feed_dict={x_data: rand_x, y_target: rand_y})
    if (i+1)%25==0:
        print('Step #' + str(i+1) + ' A = ' + str(sess.run(A)))
        print('Loss = ' + str(sess.run(loss, feed_dict={x_data: rand_x, y_target: rand_y})))

# 评估准确率(loss)
mse_test = sess.run(loss, feed_dict={x_data: np.transpose([x_vals_test]), y_target: np.transpose([y_vals_test])})
mse_train = sess.run(loss, feed_dict={x_data: np.transpose([x_vals_train]), y_target: np.transpose([y_vals_train])})
print('MSE on test:' + str(np.round(mse_test, 2)))
print('MSE on train:' + str(np.round(mse_train, 2)))

# 分类算法案例
# We will create sample data as follows:
# x-data: sample 50 random values from a normal = N(-1, 1)
#         + sample 50 random values from a normal = N(1, 1)
# target: 50 values of 0 + 50 values of 1.
#         These are essentially 100 values of the corresponding output index
# We will fit the binary classification model:
# If sigmoid(x+A) < 0.5 -> 0 else 1
# Theoretically, A should be -(mean1 + mean2)/2

# 重置计算图
ops.reset_default_graph()

# 加载计算图
sess = tf.Session()

# 声明批量大小
batch_size = 25

# 创建数据集
x_vals = np.concatenate((np.random.normal(-1, 1, 50), np.random.normal(2, 1, 50)))
y_vals = np.concatenate((np.repeat(0., 50), np.repeat(1., 50)))
x_data = tf.placeholder(shape=[1, None], dtype=tf.float32)
y_target = tf.placeholder(shape=[1, None], dtype=tf.float32)

# 分割数据集 train/test = 80%/20%
train_indices = np.random.choice(len(x_vals), round(len(x_vals)*0.8), replace=False)
test_indices = np.array(list(set(range(len(x_vals))) - set(train_indices)))
x_vals_train = x_vals[train_indices]
x_vals_test = x_vals[test_indices]
y_vals_train = y_vals[train_indices]
y_vals_test = y_vals[test_indices]

# 创建变量 (one model parameter = A)
A = tf.Variable(tf.random_normal(mean=10, shape=[1]))

# Add operation to graph
# Want to create the operstion sigmoid(x + A)
# Note, the sigmoid() part is in the loss function
my_output = tf.add(x_data, A)

# 增加分类损失函数 (cross entropy)
xentropy = tf.reduce_mean(tf.nn.sigmoid_cross_entropy_with_logits(logits=my_output, labels=y_target))

# Create Optimizer
my_opt = tf.train.GradientDescentOptimizer(0.05)
train_step = my_opt.minimize(xentropy)

# Initialize variables
init = tf.global_variables_initializer()
sess.run(init)

# 运行迭代
for i in range(1800):
    rand_index = np.random.choice(len(x_vals_train), size=batch_size)
    rand_x = [x_vals_train[rand_index]]
    rand_y = [y_vals_train[rand_index]]
    sess.run(train_step, feed_dict={x_data: rand_x, y_target: rand_y})
    if (i+1)%200==0:
        print('Step #' + str(i+1) + ' A = ' + str(sess.run(A)))
        print('Loss = ' + str(sess.run(xentropy, feed_dict={x_data: rand_x, y_target: rand_y})))

# 评估预测
# 用squeeze（）函数封装预测操作，使得预测值和目标值有相同的维度。
y_prediction = tf.squeeze(tf.round(tf.nn.sigmoid(tf.add(x_data, A))))
# 用equal（）函数检测是否相等,
# 把得到的true或false的boolean型张量转化成float32型，
# 再对其取平均值，得到一个准确度值。
correct_prediction = tf.equal(y_prediction, y_target)
accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))
acc_value_test = sess.run(accuracy, feed_dict={x_data: [x_vals_test], y_target: [y_vals_test]})
acc_value_train = sess.run(accuracy, feed_dict={x_data: [x_vals_train], y_target: [y_vals_train]})
print('Accuracy on train set: ' + str(acc_value_train))
print('Accuracy on test set: ' + str(acc_value_test))

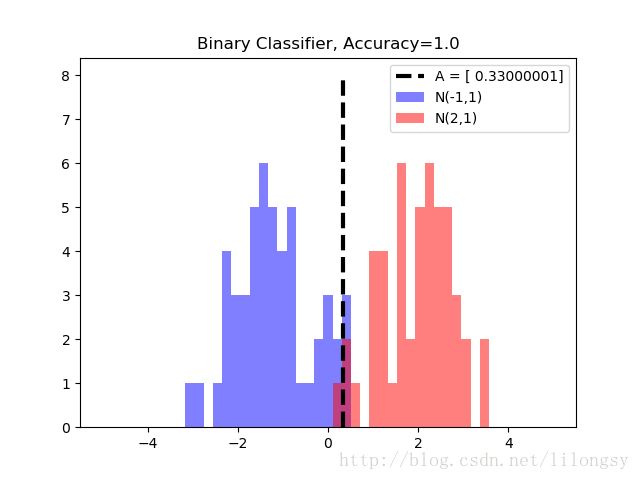
# 绘制分类结果
A_result = -sess.run(A)
bins = np.linspace(-5, 5, 50)
plt.hist(x_vals[0:50], bins, alpha=0.5, label='N(-1,1)', color='white')
plt.hist(x_vals[50:100], bins[0:50], alpha=0.5, label='N(2,1)', color='red')
plt.plot((A_result, A_result), (0, 8), 'k--', linewidth=3, label='A = '+ str(np.round(A_result, 2)))
plt.legend(loc='upper right')
plt.title('Binary Classifier, Accuracy=' + str(np.round(acc_value_test, 2)))
plt.show()

输出：

Step #25 A = [[ 5.79096079]]
Loss = 16.8725
Step #50 A = [[ 8.36085415]]
Loss = 3.60671
Step #75 A = [[ 9.26366138]]
Loss = 1.05438
Step #100 A = [[ 9.58914948]]
Loss = 1.39841
MSE on test:1.04
MSE on train:1.13
Step #200 A = [ 5.83126402]
Loss = 1.9799
Step #400 A = [ 1.64923656]
Loss = 0.678205
Step #600 A = [ 0.12520729]
Loss = 0.218827
Step #800 A = [-0.21780498]
Loss = 0.223919
Step #1000 A = [-0.31613481]
Loss = 0.234474
Step #1200 A = [-0.33259964]
Loss = 0.237227
Step #1400 A = [-0.28847221]
Loss = 0.345202
Step #1600 A = [-0.30949864]
Loss = 0.312794
Step #1800 A = [-0.33211425]
Loss = 0.277342
Accuracy on train set: 0.9625
Accuracy on test set: 1.0