OpenCV

• OpenCV是一个开源的计算机视觉库，可以从 http://opencv.org 获取。
• OpenCV 库用C语言和 C++ 语言编写，可以在 Windows、Linux、Mac OS X 等系统运行。同时也在积极开发 Python、Java、Matlab 以及其他一些语言的接口，将库导入安卓和 iOS 中为移动设备开发应用。
• OpenCV 设计用于进行高效的计算，十分强调实时应用的开发。它由 C++ 语言编写并进行了深
  度优化，从而可以享受多线程处理的优势。
• OpenCV 的一个目标是提供易于使用的计算机视觉接口，从而帮助人们快速建立精巧的视觉应用。
• OpenCV 库包含从计算机视觉各个领域衍生出来的 500 多个函数，包括工业产品质量检验、医学图像处理、安保领域、交互操作、相机校正、双目视觉以及机器人学

opencv大坑之BGR
opencv对于读进来的图片的通道排列是BGR，而不是主流的RGB！谨记！

#opencv读入的矩阵是BGR，如果想转为RGB，可以这么转
img4 = cv2.imread('1.jpg')
 img4 = cv2.cvtColor(img4,cv2.COLOR_BGR2RGB)

OpenCV与其他算法比较

• 除了opencv读入的彩色图片以BGR顺序存储外，其他所有图像库读入彩色图片都以RGB存储。
• 除了PIL读入的图片是img类之外，其他库读进来的图片都是以numpy 矩阵。
• 各大图像库的性能，最好的OpenCv，无论是速度还是图片操作的全面性，都属于碾压的存在，毕竟他是一个巨大的cv专用库。
  
  OpenCV常见算法

1. 图像的基本操作读取、显示、存储：通过调用OpenCV中的cv2.imread()，cv2.imshow()，cv2.write()分别实现。
2. 在OpenCV中实现将彩色像素转化为灰度像素。图像的几何变换：平移、缩放、旋转、插值（最近邻、双线性）。
3. 对比增强：线性变换、伽马变换、直方图均衡化。
4. 边缘检测：Sobel、Canny
5. 图像的二维滤波：cvFilter2D

线性回归
什么是线性回归？
举个例子，某商品的利润在售价为2元、5元、10元时分别为4元、10元、20元，我们很容易得出商品的利润与售价的关系符合直线：y=2x.
在上面这个简单的一元线性回归方程中，我们称“2”为回归系数，即斜率为其回归系数。
回归系数表示商品的售价(x)每变动一个单位，其利润(y)与之对应的变动关系。

线性回归表示这些离散的点**总体上“最逼近”**哪条直线。

线性回归–最小二乘法（Least Square Method）

• 它通过最小化误差的平方和，寻找数据的最佳函数匹配。
• 利用最小二乘法可以简便地求得未知的数据，并使得这些求得的数据与实际数据之间误差的平方
  和为最小。
• 假设我们现在有一系列的数据点(xi,yi) (i=1,…,m)，那么由我们给出的拟合函数h(x)得到的估计量就
  是h(xi)
• 残差：ri = h(xi) – yi

• 拟合程度，用通俗的话来讲，就是我们的拟合函数h(x)与待求解的函数y之间的相似性。那么2-范数越小，自然相似性就比较高了。

由此，我们可以写出最小二乘法的定义了：

这是一个无约束的最优化问题，分别对k和b求偏导，然后令偏导数为0，即可获得极值点。

RANSAC

RANSAC思想

• 随机采样一致性（random sample consensus）。
• RANSAC是一种思想，一个求解已知模型的参数的框架。它不限定某一特定的问题，可以是计算机视觉的问题，同样也可以是统计数学，甚至可以是经济学领域的模型参数估计问题。
• 它是一种迭代的方法，用来在一组包含离群的被观测数据中估算出数学模型的参数。 RANSAC是一个非确定性算法，在某种意义上说，它会产生一个在一定概率下合理的结果，其允许使用更多次的迭代来使其概率增加。
• RANSAC的基本假设是 “内群”数据可以通过几组模型参数来叙述其数据分布，而“离群”数据则是不适合模型化的数据。 数据会受噪声影响,噪声指的是离群，例如从极端的噪声或错误解释有关数据的测量或不正确的假设。RANSAC假定，给定一组（通常很小的）内群，存在一个程序，这个程序可以估算最佳解释或最适用于这一数据模型的参数。
  
  RANSAC与最小二乘法
• 生产实践中的数据往往会有一定的偏差。
• 例如我们知道两个变量X与Y之间呈线性关系，Y=aX+b，我们想确定参数a与b的具体值。通过实验，可以得到一组X与Y的测试值。虽然理论上两个未知数的方程只需要两组值即可确认，但由于系统误差的原因，任意取两点算出的a与b的值都不尽相同。我们希望的是，最后计算得出的理论模型与测试值的误差最小。
• 最小二乘法：通过计算最小均方差关于参数a、b的偏导数为零时的值。事实上，很多情况下，最小二乘法都是线性回归的代名词。
• 遗憾的是，最小二乘法只适合于误差较小的情况。
• 在模型确定以及最大迭代次数允许的情况下，RANSAC总是能找到最优解。（对于包含80%误差的数据集，RANSAC的效果远优于直接的最小二乘法。）
• 由于一张图片中像素点数量大，采用最小二乘法运算量大，计算速度慢。

RANSAC的步骤
RANSAC算法的输入:

• 一组观测数据（往往含有较大的噪声或无效点），
• 一个用于解释观测数据的参数化模型，比如 y=ax+b
• 一些可信的参数。

1. 在数据中随机选择几个点设定为内群
2. 计算适合内群的模型 e.g. y=ax+b ->y=2x+3 y=4x+5
3. 把其它刚才没选到的点带入刚才建立的模型中，计算是否为内群 e.g. hi=2xi+3->ri
4. 记下内群数量
5. 重复以上步骤
6. 比较哪次计算中内群数量最多,内群最多的那次所建的模型就是我们所要求的解

注意：不同问题对应的数学模型不同，因此在计算模型参数时方法必定不同，RANSAC的作用不在于计算模型参数。（这导致ransac的缺点在于要求数学模型已知）

这里有几个问题：

1. 一开始的时候我们要随机选择多少点(n)
2. 以及要重复做多少次(k)

RANSAC的参数确定

• 假设每个点是真正内群的概率为 w：
  

RANSAC的优缺点

• 优点：

1. 它能鲁棒的估计模型参数。例如，它能从包含大量局外点的数据集中估计出高精度的参数。

• 缺点：

2. 它计算参数的迭代次数没有上限；如果设置迭代次数的上限，得到的结果可能不是最优的结果，甚至可能得到错误的结果。
3. RANSAC只有一定的概率得到可信的模型，概率与迭代次数成正比。
4. 它要求设置跟问题相关的阀值。
5. RANSAC只能从特定的数据集中估计出一个模型，如果存在两个（或多个）模型，RANSAC不能找到别的模型。
6. 要求数学模型已知

最小二乘法代码部分

import pandas as pd
import matplotlib.pyplot as plt

# 读取CSV文件
sales = pd.read_csv('train_data.csv', sep='\s*,\s*', engine='python')
X = sales['X'].values    # 存csv的第一列
Y = sales['Y'].values    # 存csv的第二列

# 初始化赋值
s1 = 0
s2 = 0
s3 = 0
s4 = 0
n = len(X)  # 使用len(X)自动获取数据长度

# 循环累加
for i in range(n):
    s1 += X[i] * Y[i]   # X*Y，求和
    s2 += X[i]          # X的和
    s3 += Y[i]          # Y的和
    s4 += X[i] ** 2     # X的平方，求和

# 计算斜率和截距
k = (n * s1 - s2 * s3) / (n * s4 - s2 ** 2)
b = (s3 - k * s2) / n

# 打印斜率和截距
print("斜率: {:.2f}, 截距: {:.2f}".format(k, b))

# 绘制数据点
plt.scatter(X, Y, color='blue', label='数据点')

# 计算拟合直线的Y值
Y_pred = k * X + b

# 绘制拟合直线
plt.plot(X, Y_pred, color='red', label='拟合直线')

# 设置图例
plt.legend()

# 设置坐标轴标签
plt.xlabel('X')
plt.ylabel('Y')

# 显示图表
plt.show()

RANSAC在最小二乘法上的应用代码

import numpy as np
import scipy as sp
import scipy.linalg as sl


def ransac(data, model, n, k, t, d, debug=False, return_all=False):
    """
    输入:
        data - 样本点
        model - 假设模型:事先自己确定
        n - 生成模型所需的最少样本点
        k - 最大迭代次数
        t - 阈值:作为判断点满足模型的条件
        d - 拟合较好时,需要的样本点最少的个数,当做阈值看待
    输出:
        bestfit - 最优拟合解（返回nil,如果未找到）
    """
    iterations = 0
    bestfit = None
    besterr = np.inf  # 设置默认值
    best_inlier_idxs = None
    while iterations < k:
        maybe_idxs, test_idxs = random_partition(n, data.shape[0])
        print('test_idxs = ', test_idxs)
        maybe_inliers = data[maybe_idxs, :]  # 获取size(maybe_idxs)行数据(Xi,Yi)
        test_points = data[test_idxs]  # 若干行(Xi,Yi)数据点
        maybemodel = model.fit(maybe_inliers)  # 拟合模型
        test_err = model.get_error(test_points, maybemodel)  # 计算误差:平方和最小
        print('test_err = ', test_err < t)
        also_idxs = test_idxs[test_err < t]
        print('also_idxs = ', also_idxs)
        also_inliers = data[also_idxs, :]
        if debug:
            print('test_err.min()', test_err.min())
            print('test_err.max()', test_err.max())
            print('numpy.mean(test_err)', np.mean(test_err))
            print('iteration %d:len(alsoinliers) = %d' % (iterations, len(also_inliers)))
        # if len(also_inliers > d):
        print('d = ', d)
        if (len(also_inliers) > d):
            betterdata = np.concatenate((maybe_inliers, also_inliers))  # 样本连接
            bettermodel = model.fit(betterdata)
            better_errs = model.get_error(betterdata, bettermodel)
            thiserr = np.mean(better_errs)  # 平均误差作为新的误差
            if thiserr < besterr:
                bestfit = bettermodel
                besterr = thiserr
                best_inlier_idxs = np.concatenate((maybe_idxs, also_idxs))  # 更新局内点,将新点加入
        iterations += 1
    if bestfit is None:
        raise ValueError("did't meet fit acceptance criteria")
    if return_all:
        return bestfit, {'inliers': best_inlier_idxs}
    else:
        return bestfit


def random_partition(n, n_data):
    """return n random rows of data and the other len(data) - n rows"""
    all_idxs = np.arange(n_data)  # 获取n_data下标索引
    np.random.shuffle(all_idxs)  # 打乱下标索引
    idxs1 = all_idxs[:n]
    idxs2 = all_idxs[n:]
    return idxs1, idxs2


class LinearLeastSquareModel:
    # 最小二乘求线性解,用于RANSAC的输入模型
    def __init__(self, input_columns, output_columns, debug=False):
        self.input_columns = input_columns
        self.output_columns = output_columns
        self.debug = debug

    def fit(self, data):
        # np.vstack按垂直方向（行顺序）堆叠数组构成一个新的数组
        A = np.vstack([data[:, i] for i in self.input_columns]).T  # 第一列Xi-->行Xi
        B = np.vstack([data[:, i] for i in self.output_columns]).T  # 第二列Yi-->行Yi
        x, resids, rank, s = sl.lstsq(A, B)  # residues:残差和
        return x  # 返回最小平方和向量

    def get_error(self, data, model):
        A = np.vstack([data[:, i] for i in self.input_columns]).T  # 第一列Xi-->行Xi
        B = np.vstack([data[:, i] for i in self.output_columns]).T  # 第二列Yi-->行Yi
        B_fit = sp.dot(A, model)  # 计算的y值,B_fit = model.k*A + model.b
        err_per_point = np.sum((B - B_fit) ** 2, axis=1)  # sum squared error per row
        return err_per_point


def test():
    # 生成理想数据
    n_samples = 500  # 样本个数
    n_inputs = 1  # 输入变量个数
    n_outputs = 1  # 输出变量个数
    A_exact = 20 * np.random.random((n_samples, n_inputs))  # 随机生成0-20之间的500个数据:行向量
    perfect_fit = 60 * np.random.normal(size=(n_inputs, n_outputs))  # 随机线性度，即随机生成一个斜率
    B_exact = sp.dot(A_exact, perfect_fit)  # y = x * k

    # 加入高斯噪声,最小二乘能很好的处理
    A_noisy = A_exact + np.random.normal(size=A_exact.shape)  # 500 * 1行向量,代表Xi
    B_noisy = B_exact + np.random.normal(size=B_exact.shape)  # 500 * 1行向量,代表Yi

    if 1:
        # 添加"局外点"
        n_outliers = 80
        all_idxs = np.arange(A_noisy.shape[0])  # 获取索引0-499
        np.random.shuffle(all_idxs)  # 将all_idxs打乱
        outlier_idxs = all_idxs[:n_outliers]  # 80个0-500的随机局外点
        A_noisy[outlier_idxs] = 20 * np.random.random((n_outliers, n_inputs))  # 加入噪声和局外点的Xi
        B_noisy[outlier_idxs] = 50 * np.random.normal(size=(n_outliers, n_outputs))  # 加入噪声和局外点的Yi
    # setup model
    all_data = np.hstack((A_noisy, B_noisy))  # 形式([Xi,Yi]....) shape:(500,2)500行2列
    input_columns = range(n_inputs)  # 数组的第一列x:0
    output_columns = [n_inputs + i for i in range(n_outputs)]  # 数组最后一列y:1
    debug = False
    model = LinearLeastSquareModel(input_columns, output_columns, debug=debug)  # 类的实例化:用最小二乘生成已知模型

    linear_fit, resids, rank, s = sp.linalg.lstsq(all_data[:, input_columns], all_data[:, output_columns])

    # run RANSAC 算法
    ransac_fit, ransac_data = ransac(all_data, model, 50, 1000, 7e3, 300, debug=debug, return_all=True)

    if 1:
        import pylab

        sort_idxs = np.argsort(A_exact[:, 0])
        A_col0_sorted = A_exact[sort_idxs]  # 秩为2的数组

        if 1:
            pylab.plot(A_noisy[:, 0], B_noisy[:, 0], 'b.', label='data')  # 散点图使用绿色点表示
            pylab.plot(A_noisy[ransac_data['inliers'], 0], B_noisy[ransac_data['inliers'], 0], 'kx', label="RANSAC data")
        else:
            pylab.plot(A_noisy[non_outlier_idxs, 0], B_noisy[non_outlier_idxs, 0], 'b.', label='noisy data')
            pylab.plot(A_noisy[outlier_idxs, 0], B_noisy[outlier_idxs, 0], 'r.', label='outlier data')

        pylab.plot(A_col0_sorted[:, 0],
                   np.dot(A_col0_sorted, ransac_fit)[:, 0],
                   label='RANSAC fit')
        pylab.plot(A_col0_sorted[:, 0],
                   np.dot(A_col0_sorted, perfect_fit)[:, 0],
                   label='exact system')
        pylab.plot(A_col0_sorted[:, 0],
                   np.dot(A_col0_sorted, linear_fit)[:, 0],
                   label='linear fit')
        pylab.legend()
        pylab.show()

if __name__ == "__main__":
    test()

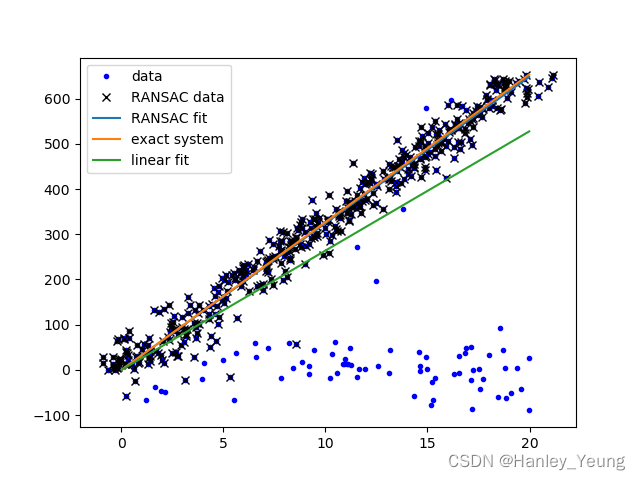
• 绿色直线表示直接使用最小二乘法时的回归方程
• 橙色直线表示没有噪音时的回归方程
• 蓝色直线（几乎与橙色重合）表示在RANSAC框架下使用的最小二乘法得到的回归方程