简介

官网

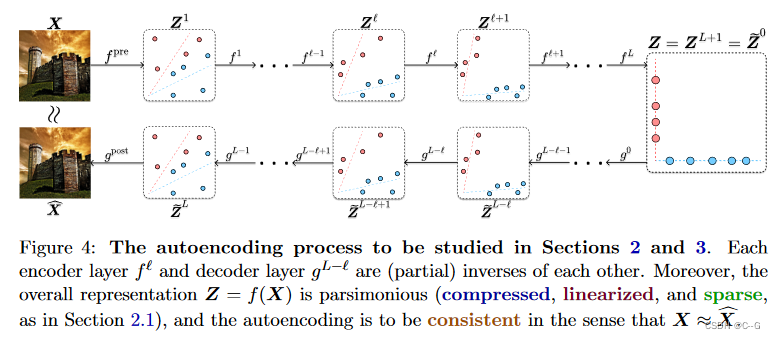
 提出了一种新的白盒Transformer架构，名为 CRATE，通过压缩和稀疏化操作来实现数据的表示学习。这种架构的设计使得内部表示更易解释，相比于黑盒Transformer，CRATE的内部表示具有更清晰和易提取的语义含义。

 通过最大化 coding rate reduction——∆R(z)，可以促使特征 $z_i$ 被紧凑地编码为低维高斯分布的混合物，其中不同的高斯分布在统计上是不相关的。

 还探讨了压缩和去噪之间的联系，指出去噪等价于学习数据分布的表示。因此提出了一种结构化的去噪-扩散理论，以此来构建一致的编码器-解码器对 f, g。这一理论通过与压缩框架相连接，从而定义了结构化扩散去噪范式。

表征学习——压缩和稀疏化

 学习特征表示的一个原则度量是所谓的稀疏率降低，它同时表征表征的内在信息增益和外在稀疏性。其目标是找到一个特征映射函数 f，将具有潜在非线性和多模态分布的输入数据 $X\in R^{D\times N}$,转换为简洁的特征表示 $Z\in R^{d\times n}$。

 学习表征的完整要求是:

1. 紧凑编码：数据应该被严格地分布在与数据的内在低维结构相匹配的标准低维结构中，以确保对数据进行紧凑编码。
2. 线性化：低维结构应具有（分段）线性几何，以便于在表示空间中进行插值和外推。
3. 稀疏性：对应于数据分布不同部分的低维结构应该在统计上是不相关的或几何上是正交的，并且是轴对齐的，以确保更紧凑的编码，便于下游处理。
4. 一致性：为了自编码/生成的目的，学习到的表示是可逆的，可以解码特征以恢复相应的输入数据，无论是在个体样本的层面上还是在分布层面上。

 也就是输入X经过压缩和稀疏化得到特征表示Z，Z经过解码得到$\hat{X}$，要求$\hat{X}$近似X。

信息增益

 先前工作提出通过最大化信息增益来获得简约表示，这是对特征信息内容的原则性度量。而信息增益的一个具体实例是特征的编码率降低。

 回到自动编解问题，设 $Z=[z_1,\cdots ,z_n^{\prime }]\in R^{d\times n}$为矩阵值随机变量。对 Z 施加以下统计模型，参数化为标准正交基 $U_{[K]}=(U_k{)}_{k\in [K]}\in (R^{d\times p}{)}^K$ :每个令牌 $z_i$ 的边际分布表示为：

式中$(s_i{)}_{i\in [n]}\in [K{]}^n$ 是对应于子空间指标的随机变量，$(a_i{)}_{i\in [n]}\in (R^p{)}^n$是零均值高斯变量。

 如果有选择地指定一个噪声参数 σ≥0，意味着用高斯噪声“扩散”标记 : 每个令牌 $z_i$ 的边际分布表示为：

 我们希望这些代码在每个子空间内具有高斯边缘分布，类似于(8)可以计算出这些码的编码率。

降低稀疏率

 对于表示和子空间的任意联合旋转，速率降低是不变的。
 优化速率降低可能不会自然地导致轴对齐(即稀疏)表示。
 因此，通过变换表示(及其支持的子空间)，使特征 Z 最终相对于结果表示空间的标准坐标变得稀疏。优化目标为：

等价于：

为了更好的可计算性，将 $l^0$范数松弛为 $l^1$ 范数。

流行的一类执行最大似然估计的模型是基于能量的模型。
而总体目标函数(17)具有作为“能量函数”的解释。
如果假设代理似然是精确的(直到常数)，则特征集 Z 的期望概率分布在常数范围内为

压缩和稀疏化

 公式17在计算上很难优化。因此，采取一种近似方法，通过多个(例如L)的串联来实现全局转换 f，简单的增量和局部操作 $f^l$，将表示分布推向所需的精简模板分布:

这个过程如下图所示：

由$Z^{l+1}=f^l(Z^l)$：

从概念上讲，如果遵循ReduNet的思想，每个 $f^l$ 应该进行类似于“梯度上升”的操作:

 注意，$p(Z|U_{[k]})$在公式18里定义了。可以看到，$▽lo{g}_p(Z|U_{[K]})$类似于一个分数函数，更新(23)类似于一个去噪过程。这个过程后续再详细介绍。

 已经有工作证实，很难直接计算梯度并优化速率降低项 $\Delta R$，因此选择一个具有强大概念基础的两步交替最小化过程。

对于第一步公式(24)，通过一个近似的梯度步骤 压缩 标记 $Z^l$，以最小化编码率 $R^c(Z^l|U_{[K]}^l)$ 的估计值。

不幸的是,编码率 $▽R^c$ 的梯度计算代价高昂，使用 MSSA(·) 操作符去近似梯度。

对于第二步公式(25)，对压缩令牌进行 稀疏化。

可以通过迭代 shrinkagethreshold 算法(ISTA)来实现这一步骤。

重复应用 压缩 和 稀疏，这些操作形成了网络的层。

过程如下：

MSSA 和 ISTA

MSSA

对于第一步，通过最小化编码率 $R^c$ 的上界来压缩 K 个子空间的标记集:

压缩算子在 $R^c$ 上采取近似的梯度下降步骤，$R^c(Z|U_{[k]})$ 的梯度近似为：

 由于(31)中的表达式精确计算成本很高，因为它需要K矩阵逆，使得在大规模问题上难以使用朴素梯度下降法。因此，寻求这个梯度的有效近似值;选择使用第一个诺伊曼级数:

 近似梯度表达式（32）近似了每个投影标记特征 $U_k^{\ast }{z}_i$ 由其他标记特征 $U_k^{\ast }{z}_j$ 回归的残差。这种自回归中并非所有标记特征都来自同一子空间。因此，为了将每个标记特征与其自身组的标记特征进行压缩，通过 $(U_k^{\ast }Z)\ast (U_k^{\ast }Z)$ 在投影特征之间进行自相关计算它们的相似性，然后通过 $softmax((U_k^{\ast }Z)\ast (U_k^{\ast }Z))$ 将其转换为成员的分布。

 因此，如果只使用相似的标记来相互回归和去噪，那么具有学习率 κ 的编码率的梯度步长可以近似如下:

MSSA 通过 SSA 操作符定义为:

SSA 算子类似于典型Transformer中的注意算子, value,key 和 query 线性算子都被设置为与子空间基相同，即 $V_k=K_k=Q_k=U_k^{\ast }$。

ISTA

第二步中有公式(25)

 梯度 $\nabla R(Z)$ 涉及矩阵逆，因此求解(25)的朴素近端梯度在大规模问题上变得难以处理。因此，采取了一种简化的方法来权衡表征多样性和稀疏化:假设一个(完全)不相干或正交字典 $D^l\in R^{d\times d}$，并要求 $Z^{l+1/2}$ 相对于 $D^l$ b进行稀疏化。即$Z^{l+1/2}\approx D^l{Z}^{l+1}$，其中 $Z^{l+1}$ 更稀疏; 也就是说，它是 $Z^{l+1/2}$ 的稀疏编码。字典 $D^l$ 用于同时稀疏化所有标记。根据不相干假设， $(D^l)\ast (D^l)\approx I$。根据公式（8）有：

用以下程序求解(25):

上述稀疏表示通常通过将其松弛为无约束凸规划来解决，称为LASSO

对 $Z^{l+1}$ 加入一个非负约束，求解相应的非负LASSO

通过执行一个展开的近端梯度下降步骤，即 ISTA 步骤，对(41)进行增量优化:

CRATE

结合MSSA，ISTA，可以得到如下基于速率降低的Transformer层：

如下图所示，得到一个白盒Transformer架构。

基于结构化去噪和扩散的白盒解码

 假设 $z_{♮}^l$ 表示编码过程第 $l$ 层的任何令牌的边际分布，$z^l$的噪声表示为 $z^l=z_{♮}^l+{\sigma }^l\omega$。结合公式10，对$z^l$ 减噪以恢复 $z_{♮}^l$，最优估计值为 $E[z_{♮}^l|z^l]$，其封闭形式表示为：

 上述公式解释为在噪声水平 ${\sigma }^l$ 上通过分数函数 $▽logx{q}^l$ 的梯度上升步骤去噪。分数函数用于从 restricted parametric family 中学习数据分布。对于某些广泛的parametric families，分数函数是可有效计算的，例如mixture of Gaussians, independent component analysis models, over-complete dictionary learning。

 那么假设 $z_{♮}^l$ 有如公式（10）的 lowdimensional Gaussian 混合分布，而 $z^l$ 则是公式（11）的分布，结合公式45以及一些假设，可以得到分数函数 $▽logx{q}^l$ 的封闭表达式。

 公式（46）中的操作类似于标准Transformer体系结构中的自关注层，具有K个头，序列长度 n = 1，“query-key-value”被令牌 $z^l$ 的单个线性投影 $U_k^{\ast }{z}^l$ 替换。

随机去噪

 公式（46）是一次去噪，在一个扩散过程中，当 $T=({\sigma }^l{)}^2>0$ 以时间 $t\in [0,T]$为指标，将 $z_{♮}^l$ 转换为噪声分布 $z^l$。

 $(w_t{)}_{t\in [0,T]}$ 是一个 Wiener 过程，式(47)中将该过程表示为随机微分方程(SDE)，该SDE具有唯一的解，其分布为 $z_t\stackrel{\mathrm{d}}{=}{z}_{♮}^l+{\omega }_t$。$(w_t{)}_{t\in [0,t]}$ 是一个Wiener过程，因此 $w_t$ 分布为 $N(0,tI)$，使得 $z_T=z_{({\sigma }^l{)}^2}\stackrel{\mathrm{d}}{=}{z}^l$，用$q_t$表示 $z_t$ 的密度，则随机过程 $(z_t^{\leftarrow }{)}_{t\in [0,T]}$，其中 $z_t^{\leftarrow }\stackrel{\cdot }{=}{z}_{T-t}$的唯一解如下SDE:

 $w_t^{\leftarrow }$是另一个 Wiener 过程。因为 $(z_{T-t}{)}_{t\in [0,T]}$ 解决了公式 (48)，这个过程产生了 $z_{♮}^l$的一个表示。更重要的是，可以严格地证明，迭代去噪-扩散过程(48)对于有效地表示高维多模态数据分布是充分且必要的。

确定性去噪

 公式(48)的每个无限小更新类似于公式(45)，它在“扩散”对数似然上采取单个梯度步骤来去噪。因此，将该过程(48)解释为随机去噪过程。在实践中，需要对该过程进行确定性模拟。概率流ODE提供了这样一个过程。公式(48)中 $z_t^{\leftarrow }$ 的动态概率密度与ODE相同。

 由公式(49)提供的 $z_{♮}^l$ 的表示可以简单地表征为跨多个噪声尺度的迭代去噪。这就引出了扩散去噪的核心观点:

去噪相当于学习数据分布的表示。

结构化扩散去噪

 在低噪声水平下，对local signal model $U_{[k]}^l$ 的压缩等价于对local signal model的去噪。从确定性去噪过程(49)的角度来看，这在压缩项 $R_c$ 的梯度和 Gaussian codebook model 的分数函数之间建立了联系。最重要的是，这能够从不同的角度理解crate编码器的MSSA算子，通过去噪实现数据分布向local signal model的增量转换。这一重要性质保证了相应的确定性扩散过程——即去噪过程的时间反转(49)——隐含了由MSSA实现的压缩操作的逆算子。

 给定第 $l$ 层即 $Z^l$ 的令牌分布表示，构造了一个与公式(49)相同的确定性结构化去噪过程，该过程将数据压缩到表示 f 的第 $l$ 层即 $U_{[k]}^l$ 的local signal model，在小时间尺度 T > 0 上用$R_c$ 表示这个结构化去噪过程。

 该过程在 t = 0 时的信号模型(10)与 t = T 时的信号模型的噪声版本之间进行插值。扩散过程的时间反转得到一个结构化的扩散过程，它将signal model转化为一个增量的噪声更大的版本。

 这两个过程在分配意义上是相互对立的。为了将这些结构化的去噪和扩散过程用于表示学习，可以大胆地将第一层分布 $Z^1=f^{pre}(X)$ 本身视为与第一个local signal model $U_{[k]}^1$ 分布的一个小偏差。到目前为止在单个“层”上研究的增量构造表示，得到以下结构化去噪过程，其中层指标 $l$ 和时间 t 统一为单个参数，其中 $Z(0)=Z^1$为预处理后的数据分布:

同样的有逆过程，一个结构化的扩散过程。

 这两个方程为使用去噪扩散理论将数据转换为结构化的、简洁的表示提供了概念基础。

• 它们相似的函数形式——通过压缩梯度$▽R^c$——表明结构化去噪和结构化扩散所需的算子本质上是相同的形式。
• 在速率降低目标的压缩项的梯度和类Transformer网络层之间建立的联系意味着类Transformer架构足以用于压缩编码和解码。因此，可以用完全数学可解释的网络体系结构实现压缩自动编码。

基于可逆Transformer层的结构化去噪扩散

 上面提出了一种通过展开优化来构建类似白盒Transformer的编码器网络的方法，该方法旨在根据学习到的几何和统计结构压缩数据，例如针对令牌分布，其中每个令牌作为 $U_{[K]}$支持的 Gaussian mixture。此外，建立了一个continuous-time deterministic dynamical system，它实现了结构化去噪，因为它将初始数据去噪到所需的简约结构。

为了构建网络架构，使用该过程的一阶离散化，得到了迭代。

 为了执行结构化去噪，同时确保表示结构(例如，支持子空间)本身是稀疏的，为特征插入一个稀疏化步骤。即，实例化一个可学习字典 $D^l\in R^{d\times d}$ 并对其进行稀疏化，得到：

这就产生了第 $l$ 编码器层 $f^l$ 的两步迭代，其中 $Z^{l+1}=f^l(z^l)$。

 这与crate编码器中的层是相同的。因此，这从另一个有用的角度重新导出了crate编码器层，即结构化去噪。同时已经证明了结构化去噪和展开优化之间的等价性，这源于这样一个事实，即扩散概率流在概念上和机械上类似于某些情况下压缩目标上的梯度流。因此，已经证明了离散扩散过程和展开优化之间的概念联系，即根据学习到的数据结构对信号进行迭代压缩或去噪。

结构化扩散的白盒解码器层

 编码器是由公式(52)中给出的结构化去噪ODE的离散化构造的。它的路径时间反转，反转结构化去噪ODE引起的数据分布的变换，由结构化扩散ODE正式给出:

因此使用结构化扩散ODE作为解码器的骨干。对该ODE进行一阶离散化，得到迭代式:

式中 $V_{[k]}^l$ 和每个 $V_k^l\in R^{d\times p}$ 是要“反压缩”的子空间的基。为了反转稀疏化 ISTA(·) 步的影响，实例化一个可学习的合成字典 $E^l\in R^{d\times d}$ 并乘以它，得到迭代式:

这构造了解码器的 $(l+1{)}^{st}$ 层 $g^l$:

White-Box Transformers via Sparse Rate Reduction

编码器和解码器层的图形化并加上层规范化以匹配实现描述如下图所示