通俗理解概率密度函数
·
0、前言
概率密度函数是描述连续随机变量的分布的工具，但是因为它是个“密度”，没有概率分布那么直观，下面就用通俗的说法理解概率密度函数。
1、从离续变量出发
1.1 离散随机变量
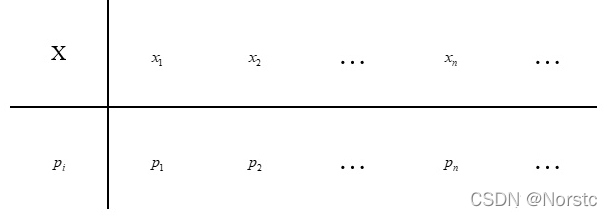
对于离散随机变量，顾名思义，随机变量的取值是离散的，如：
1.2 离散随机变量的概率分布
指离散随机变量每个取值的概率，即：
1.3 离散随机变量的累积分布函数
定义为：
表示随机变量的取值值小于等于自变量的值的概率的和。
2.连续随机变量的概率分布
2.1 连续随机变量
连续随机变量即随机变量的取值是连续的，如：
2.2 连续随机变量的概率密度函数与理解
连续随机变量的概率密度函数表示了连续随机变量的概率分布。
一下图片展示了从离散变量的概率分布拟合概率密度函数的图片：
从离散分布看，某个随机变量值的离散分布的函数值，代表随机变量取该值的概率。
但是某一个值的概率密度函数的值并不代表概率等于该值的概率，因为概率密度函数满足：
。
那如何理解概率密度函数呢？
首先，如果取连续随机变量取值的某一点，那么它的概率是接近0的。最简单但是粗略的，从长度来看，一点相对于区间，就趋近于0。
所以连续随机变量取值的概率，不仅和概率密度函数相关，还和区间长度相关。
所以便有了概率密度函数求和公式。
如上图，概率密度函数曲线在0附近最大，说明什么呢？
那就说明，连续随机变量的值在0附近的概率较大，但是并不能说明连续随机变量等于0的概率是多少。
对于连续随机变量，撇开区间谈概率，都是趋近于0。
旨在为数千万中国开发者提供一个无缝且高效的云端环境，以支持学习、使用和贡献开源项目。
更多推荐
20
0- 0
已为社区贡献16条内容
所有评论(0)