DPO

DPO(Direct Preference Optimization)出自2023年5月的斯坦福大学研究院的论文《Direct Preference Optimization: Your Language Model is Secretly a Reward Model》，大概是2023-2024年最广为人知的RLHF的替代对齐方法了。DPO的主要思想是在强化学习的目标函数中建立决策函数与奖励函数之间的关系，以规避奖励建模的过程。

DPO目标函数的推导过程如下：

在RLHF里使用PPO优化的目标函数如下（($r(x,y)$是奖励函数，参考模型为${\pi }_{\text{ref}}$，策略模型为${\pi }_{\theta }$后面简写为$\pi$）：
$$\underset{{\pi }_{\theta }}{\max }{\mathbb{E}}_{x\sim \mathcal{D},y\sim {\pi }_{\theta }(y|x)}[r(x,y)]-\beta {\mathbb{D}}_{KL}[{\pi }_{\theta }(y|x)||{\pi }_{\text{ref}}(y|x)](1)$$
接下来对上式做推导来得到最优解：
$$\begin{array}{rl}\underset{\pi }{\max }{\mathbb{E}}_{x\sim \mathcal{D},y\sim \pi }[r(x,y)]-\beta {\mathbb{D}}_{KL}[\pi (y|x)||{\pi }_{\text{ref}}(y|x)]& =\underset{\pi }{\max }{\mathbb{E}}_{x\sim \mathcal{D}}{\mathbb{E}}_{y\sim \pi (y|x)}\left[r(x,y)-\beta \log \frac{\pi (y|x)}{{\pi }_{\text{ref}}(y|x)}\right]\\ & =\underset{\pi }{\min }{\mathbb{E}}_{x\sim \mathcal{D}}{\mathbb{E}}_{y\sim \pi (y|x)}\left[\log \frac{\pi (y|x)}{{\pi }_{\text{ref}}(y|x)}-\frac{1}{\beta }r(x,y)\right]\\ & =\underset{\pi }{\min }{\mathbb{E}}_{x\sim \mathcal{D}}{\mathbb{E}}_{y\sim \pi (y|x)}\left[\log \frac{\pi (y|x)}{\frac{1}{Z(x)}{\pi }_{\text{ref}}(y|x)\exp \left(\frac{1}{\beta }r(x,y)\right)}-\log Z(x)\right](2)\end{array}$$

上面式中的$Z(x)$是一个配分函数，具体定义如下：
$$Z(x)=\sum _y{\pi }_{\text{ref}}(y|x)\exp \left(\frac{1}{\beta }r(x,y)\right)$$
注意到配分函数只是x和参考模型为${\pi }_{\text{ref}}$的函数，与策略模型$\pi$无关，我们定义下式表示的函数，它是一个有效的概率分布因为满足条件：1.对所有y有${\pi }^{\ast }(y|x)\ge 0$，2.${\sum }_y{\pi }^{\ast }(y|x)=1$ 。
$${\pi }^{\ast }(y|x)=\frac{1}{Z(x)}{\pi }_{\text{ref}}(y|x)\exp \left(\frac{1}{\beta }r(x,y)\right)$$
因为$Z(x)$不是关于y的函数，将前面的式(2)重新组织成：
$$\begin{gathered} \underset{\pi }{\min }{\mathbb{E}}_{x\sim \mathcal{D}}{\mathbb{E}}_{y\sim \pi (y|x)}\left[\log \frac{\pi (y|x)}{\frac{1}{Z(x)}{\pi }_{\text{ref}}(y|x)\exp \left(\frac{1}{\beta }r(x,y)\right)}-\log Z(x)\right]= \\ \underset{\pi }{\min }{\mathbb{E}}_{x\sim \mathcal{D}}\left[{\mathbb{E}}_{y\sim \pi (y|x)}\left[\log \frac{\pi (y|x)}{{\pi }^{\ast }(y|x)}\right]-\log Z(x)\right]= \\ \underset{\pi }{\min }{\mathbb{E}}_{x\sim \mathcal{D}}\left[{\mathbb{D}}_{KL}(\pi (y|x)||{\pi }^{\ast }(y|x))-\log Z(x)\right] \end{gathered}$$
因为$Z(x)$不依赖于策略模型$\pi$，所以上式的最小值只与KL散度项有关，根据Gibbs不等式只有当且仅当两个分布一样时KL散度取得最小值0，所以可得到最优解为：
$$\pi (y|x)={\pi }^{\ast }(y|x)=\frac{1}{Z(x)}{\pi }_{\text{ref}}(y|x)\exp \left(\frac{1}{\beta }r(x,y)\right)(3)$$
此时的解即使可以使用真实奖励函数$r^{\ast }$的MLE估计$r_{\varphi }$，但是估计配分函数$Z(x)$依然很难，所以DPO作者进一步对式(3)进行重新组织，使得奖励函数可以由相应的最优策略模型${\pi }_r$、参考策略模型${\pi }_{\text{ref}}$和$Z(x)$来表示。首先对上面式(3)两边取对数，并移项得到奖励的估计值。
$$\begin{array}{rl}& {\pi }_r(y\mid x)=\frac{1}{Z(x)}{\pi }_{\text{ref }}(y\mid x)\exp \left(\frac{1}{\beta }r(x,y)\right)\\ \Rightarrow & \log \left({\pi }_r(y\mid x)\right)=\log \left(\frac{1}{Z(x)}{\pi }_{\text{ref }}(y\mid x)\exp \left(\frac{1}{\beta }r(x,y)\right)\right)\\ \Rightarrow & \log \left({\pi }_r(y\mid x)\right)-\log \left(\frac{1}{Z(x)}\right)-\log \left({\pi }_{\text{ref }}(y\mid x)\right)=\log \left(\exp \left(\frac{1}{\beta }r(x,y)\right)\right)\\ \Rightarrow & r(x,y)=\beta \log \left(\frac{{\pi }_r(y\mid x)}{{\pi }_{\text{ref }}(y\mid x)}\right)+\beta \log (Z(x)).(4)\end{array}$$
因为Bradley-Terry (BT)模型规定人类偏好分布$p^{\ast }$​可以表示为下式：
$$\begin{gathered} p^{\ast }(y_1\succ y_2|x)=\frac{exp(r^{\ast }(x,y_1))}{exp(r^{\ast }(x,y_1))+exp(r^{\ast }(x,y_2))} \\ =\frac{1}{1+\frac{exp(r^{\ast }(x,y_2))}{exp(r^{\ast }(x,y_1))}}(5) \end{gathered}$$
将奖励估计值式(4)代入到式(5)中：
$$\begin{array}{rl}{p}^{\ast }(y_1\succ y_2|x)& =\frac{1}{1+\frac{exp(\beta \log \left(\frac{{\pi }_{\ast }(y_2\mid x)}{{\pi }_{\text{ref }}(y_2\mid x)}\right)+\beta \log (Z(x)))}{exp(\beta \log \left(\frac{{\pi }_{\ast }(y_1\mid x)}{{\pi }_{\text{ref }}(y_1\mid x)}\right)+\beta \log (Z(x)))}}\\ & =\frac{1}{1+exp(\beta \log \left(\frac{{\pi }_{\ast }(y_2\mid x)}{{\pi }_{\text{ref }}(y_2\mid x)}\right)-\beta \log \left(\frac{{\pi }_{\ast }(y_1\mid x)}{{\pi }_{\text{ref }}(y_1\mid x)}\right))}\\ & =\sigma \left(\beta \log \left(\frac{{\pi }_{\ast }(y_1\mid x)}{{\pi }_{\text{ref }}(y_1\mid x)}\right)-\beta \log \left(\frac{{\pi }_{\ast }(y_2\mid x)}{{\pi }_{\text{ref }}(y_2\mid x)}\right)\right)\end{array}$$
于是通过建模人类偏好数据，DPO的最终优化目标如下式：
$$L(\theta )=-{\mathbb{E}}_{(x,y_w,y_l)\sim \mathcal{D}}\left[\sigma \left(\beta \log \left(\frac{{\pi }_{\theta }(y_w\mid x)}{{\pi }_{\text{ref }}(y_w\mid x)}\right)-\beta \log \left(\frac{{\pi }_{\theta }(y_l\mid x)}{{\pi }_{\text{ref }}(y_l\mid x)}\right)\right)\right](6)$$
DPO算法分析：

尝试分析DPO的目标函数的导数来理解DPO算法如何对LLM的参数进行优化，先设$u=\beta \log \left(\frac{{\pi }_{\theta }(y_w\mid x)}{{\pi }_{\text{ref }}(y_w\mid x)}\right)-\beta \log \left(\frac{{\pi }_{\theta }(y_l\mid x)}{{\pi }_{\text{ref }}(y_l\mid x)}\right)$， 则上面DPO的目标函数式(6)的导数可以化简为：
$$\nabla L(\theta )=-\nabla {\mathbb{E}}_{(x,y_w,y_l)\sim \mathcal{D}}\left[\sigma (u)\right]=-{\mathbb{E}}_{(x,y_w,y_l)\sim \mathcal{D}}\left[\frac{\nabla \sigma (u)}{\sigma (u)}\nabla u\right](7)$$
sigmoid函数有性质$\nabla \sigma (u)=\sigma (u)(1-\sigma (u))=\sigma (u)\sigma (-u)$，我们设奖励的估计值为${\hat{r}}_{\theta }(x,y)=\beta \log \left(\frac{{\pi }_{\theta }(y\mid x)}{{\pi }_{\text{ref }}(y\mid x)}\right)$，则上式(7)可以变成：
$$\begin{array}{rl}& -{\mathbb{E}}_{(x,y_w,y_l)\sim \mathcal{D}}\left[\frac{\nabla \sigma (u)}{\sigma (u)}\nabla u\right]\\ & =-{\mathbb{E}}_{(x,y_w,y_l)\sim \mathcal{D}}\left[\sigma (-u)\nabla u\right]\\ & =-\beta {\mathbb{E}}_{\left(x,y_w,y_l\right)\sim \mathcal{D}}[\underset{\text{higher weight when reward estimate is wrong }}{\underbrace{\sigma \left({\hat{r}}_{\theta }\left(x,y_l\right)-{\hat{r}}_{\theta }\left(x,y_w\right)\right)}}[\underset{\text{increase likelihood of }{y}_w}{\underbrace{{\nabla }_{\theta }\log \pi \left(y_w\mid x\right)}}-\underset{\text{decrease likelihood of }{y}_l}{\underbrace{{\nabla }_{\theta }\log \pi \left(y_l\mid x\right)}}]],\end{array}$$
所以DPO的损失函数的梯度会增加偏好内容$y_w$的似然、降低非偏好内容$y_l$的似然。前半部分$\sigma \left({\hat{r}}_{\theta }\left(x,y_l\right)-{\hat{r}}_{\theta }\left(x,y_w\right)\right)$ 和$\beta$一起动态地控制梯度下降的步长；当策略模型更倾向于生成非偏好内容$y^l$时，${\hat{r}}_{\theta }\left(x,y_l\right)$和${\hat{r}}_{\theta }\left(x,y_w\right)$之间的差值变大，导致梯度下降的步长变大，从而进行更为激进的参数更新来避免生成$y_l$；而当策略模型倾向于生成符合人类偏好的内容$y_w$时，说明策略模型当前具有较好的参数，此时梯度的系数变小（即 $\sigma \left({\hat{r}}_{\theta }\left(x,y_l\right)-{\hat{r}}_{\theta }\left(x,y_w\right)\right)$ 的值变小）， 使得策略模型的参数的更新幅度降低，防止更新步长过大使得策略模型的性能出现震荡，增加训练的稳定性。

DPO的改进算法

IPO

IPO出自2023年10月的deepmind研究院的论文《A General Theoretical Paradigm to Understand Learning from Human Preferences》，论文定义了DPO的通用形式并调整其形式来解决过拟合问题。IPO相当于 在DPO的损失函数上添加了一个正则项，从而可以使得不使用early stopping技巧就可以使模型收敛。

其损失函数定义如下式（$\tau$与DPO里的$\beta$类似）
$$\begin{gathered} {\mathcal{L}}_{IPO}(\pi )={\mathbb{E}}_{(x,y_w,y_l)\sim \mathcal{D}}{\left(h_{\pi }(y_w,y_l,x)-\frac{{\tau }^{-1}}{2}\right)}^2 \\ {h}_{\pi }(y,y^{\prime },x)=\log \left(\frac{\pi (y|x){\pi }_{\text{ref}}(y^{\prime }|x)}{\pi (y^{\prime }|x){\pi }_{\text{ref}}(y|x)}\right) \end{gathered}$$

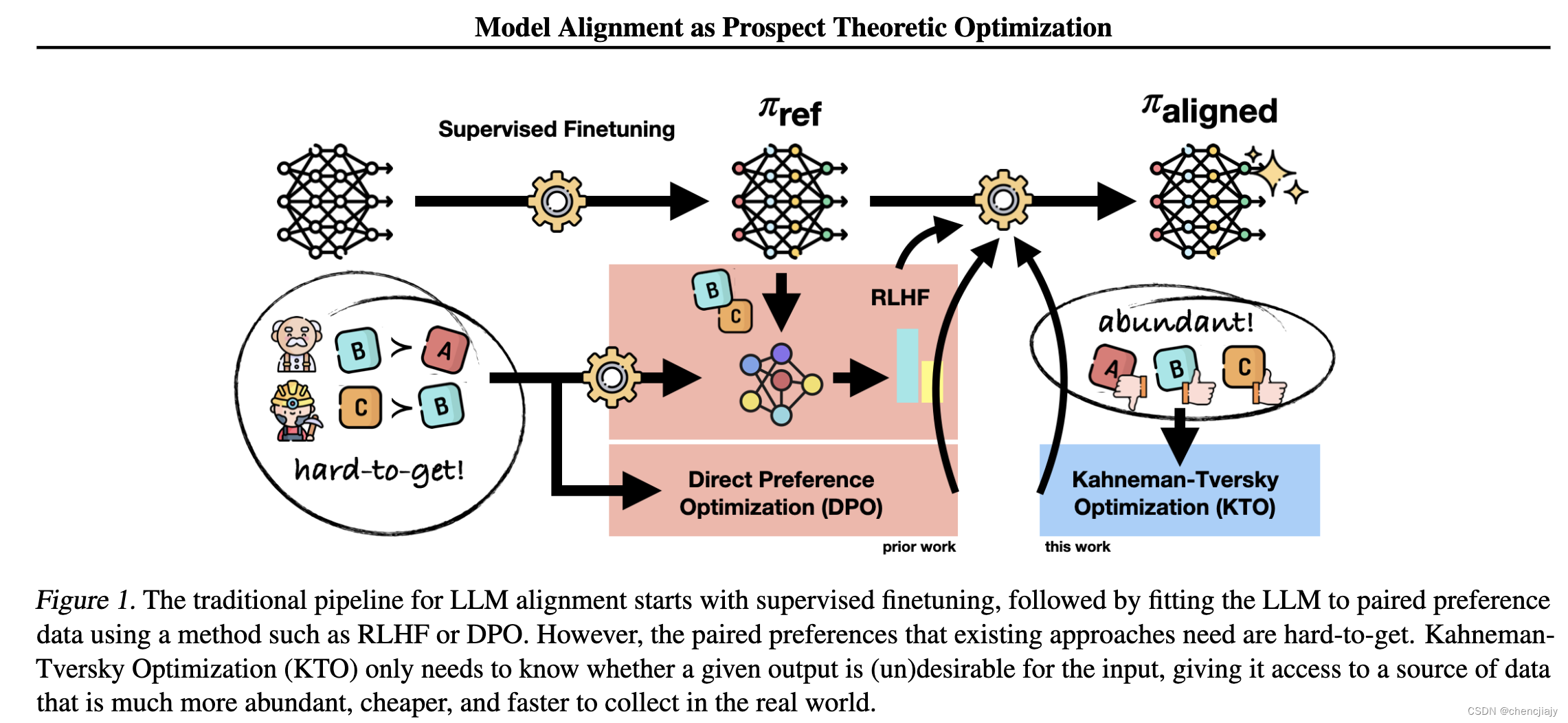
KTO

KTO(Kahneman-Tversky Optimization)出自2024年02月的论文《KTO: Model Alignment as Prospect Theoretic Optimization》

DPO等对齐方法训练时针对一个prompt需要一对偏好数据即 { x , y w , w l } \{x, y_w, w_l\} {x,yw​,wl​}​​，这个数据标注过程耗时且费力，而KTO定义的损失函数只需要将样本标注为"好(good)“或"坏(bad)”，从而使得获取标注样本的成本更低。KTO还受到Kahneman & Tversky’s prospect theory的启发，即人类倾向于用有偏但明确定义的行为来对待随机变量，比如人类有损失厌恶。

KTO的损失函数如下：
$$\begin{gathered} L_{KTO}({\pi }_{\theta },{\pi }_{\text{ref}})={\mathbb{E}}_{x,y\sim D}[w(y)(1-v_{\text{KTO}}(x,y;\beta ))] \\ {r}_{KTO}(x,y)=\beta \log \frac{{\pi }_{\theta }(y|x)}{{\pi }_{\text{ref}}(y|x)} \\ {z}_{\text{ref}}={\mathbb{E}}_{x^{\prime }\sim D}[\beta \text{KL}({\pi }_{\theta }(y^{\prime }|x^{\prime })||{\pi }_{\text{ref}}(y^{\prime }|x^{\prime }))] \\ {v}_{\text{KTO}}(x,y;\beta )=\{\begin{array}{l}\sigma (r_{\text{KTO}}(x,y)-z_{\text{ref}})\text{if}y\sim y_{\text{desirable}}|x\\ \sigma (z_{\text{ref}}-r_{\text{KTO}}(x,y))\text{if}y\sim y_{\text{undesirable}}|x\end{array} \\ w(y)=\{\begin{array}{l}{\lambda }_D\text{if}y\sim y_{\text{desirable}}|x\\ {\lambda }_U\text{if}y\sim y_{\text{undesirable}}|x\end{array} \end{gathered}$$

• 直觉上KTO有效是因为如果模型增加偏好样本的奖励时，KL散度惩罚也会增加，则损失不会增加。这将使得模型去学习如何使输出是被偏好的，使得奖励增加但是保持KL惩罚项平稳甚至降低。

• 论文中里提到实现上通过在m大小的batch上匹配输入$x^{\prime }$的不相关输出$y_U^{\prime }$后在整个batch上计算$\max \left(0,\frac{1}{m}\sum \log \frac{{\pi }_{\theta }(y_U^{\prime }|x^{\prime }}{{\pi }_{\text{ref}}(y_U^{\prime }|x^{\prime }}\right)$得到，并且对于KL惩罚项不进行反向传播使得训练更稳定，这也意味着KL惩罚项只是来控制损失的饱和程度。

• $\beta$与DPO中的含义一样，越小给模型${\pi }_{\theta }$偏离参考模型${\pi }_{\text{ref}}$的惩罚就小。作者发现$\beta =0.1$在大多数数据上表现较好。

• 设$n_D$​和$n_U$​分别代表偏好和非偏好样本的个数，使用公式$\frac{{\lambda }_D{n}_D}{{\lambda }_U{n}_U}\in [1,\frac{4}{3}]$​来设置${\lambda }_D$​和${\lambda }_U$​。

• 如果预训练模型足够好，作者们发现可以省略掉SFT过程直接进行KTO对齐微调在泛化质量上不会有损失。

CPO

CPO(Contrastive Preference Optimization)出自2024年1月的论文《Contrastive Preference Optimization: Pushing the Boundaries of LLM Performance in Machine Translation》。

CPO算法认为DPO因为有参考模型在内存使用上不够高效，并且意在缓解两个SFT在模型翻译场景应用下的缺点：1.SFT通过减少模型输出和金标准参考输出的差异使得模型性能受限于训练集的质量。2.SFT缺乏阻止模型拒绝翻译错误的机制。

CPO的损失函数由两部分组成，负对数似然损失(negative log-likelihood loss) ${\mathcal{L}}_{\text{NLL}}$和偏好损失${\mathcal{L}}_{\text{prefer}}$。
$$\begin{gathered} {\mathcal{L}}_{\text{NLL}}=-{\mathbb{E}}_{(x,y_w)\sim \mathcal{D}}[\log {\pi }_{\theta }(y_w|x)] \\ {\mathcal{L}}_{\text{prefer}}=-{\mathbb{E}}_{(x,y_w,y_l)\sim \mathcal{D}}[\log \sigma (\beta \log {\pi }_{\theta }(y_w|x)-\beta \log {\pi }_{\theta }(y_l|x)))] \\ {\mathcal{L}}_{\text{CPO}}={\mathcal{L}}_{\text{NLL}}+{\mathcal{L}}_{\text{prefer}} \end{gathered}$$

几种方法的比较

$\beta$​是这些算法共有的超参，并且对这些超参非常敏感。huggingface的一篇blog比较了DPO、KTO、IPO效果与其超参之间的关系，其结论是DPO和IPO效果差不多，相比KTO效果略好一点。

2024年4月的论文《Insights into Alignment: Evaluating DPO and its Variants Across Multiple Tasks》评估了DPO及其几种变体算法。在三种场景：1. 保留SFT过程；2.略过SFT过程；3.略过SFT过程且使用指令微调模型；以及探索了不同训练集大小对它们的影响。结论是KTO在大多数基准上比其他几种方法效果好，但是这几种方法在对齐过程中都没有显著提升模型的推理和问答能力，但是提升了数学问题解决能力。并且研究表明对齐方法对于训练数据集的大小很敏感，在小数据集上表现更好。另外对于KTO和CPO方法可以略过SFT过程。

DPO与RLHF的比较

《Policy Optimization in RLHF: The Impact of Out-of-preference Data》结论是DPO用起来方便但是泛化能力弱于RLHF，性能损失可接近一倍。（来源知乎)

《Is DPO Superior to PPO for LLM Alignment? A Comprehensive Study》 结论是PPO略好一点