关于函数或者数列极限保号性的直觉理解(图解)

欢迎大家评论区指出问题或提出更严谨、有说服力的证明
首先，贴一条很有感触的话：
“保号性”的说法，是汉语微积分教学中，穿凿附会、虚张声势的说法。 它刻意回避问题的本质，不是单刀直入、直面主题，而是有意玩弄无聊的文字游戏。
自己level有限，先不做评论，但在听了GILBERT STRANG的18.06线性代数后，确实感觉我所接受到的汉式数学教学越往高年级越反直觉，越抠定义，而GILBERT STRANG(不代表美式)的教学让人有直觉感受。

进入正题

首先说定义：
函数中的保号性：设$\underset{x\to x_0}{\lim }f(x)$存在
1.$如果A>0(或A<0),则存在\delta >0，当x\in \mathring{U}(x_0,\delta )时，f(x)>0(或f(x)<0)$

2.$如果存在\delta >0,当x\in \mathring{U}(x_0,\delta )时，f(x)\ge 0(或f(x)\le 0)时,则A\ge 0(或A\le 0)$

---

数列中的保号性：设$\underset{n\to \infty }{\lim }{x}_n存在$
1.$如果A>0(或A<0),则存在N>0，当n>N时，x_n>0(或x_n<0)$

2.$如果存在N>0,当n>N时，x_n\ge 0(或x_n\le 0)时,则A\ge 0(或A\le 0)$

由于数列算作特殊的函数，所以直接从函数入手,这里用$y=e^x$可视化。

图1

第一条

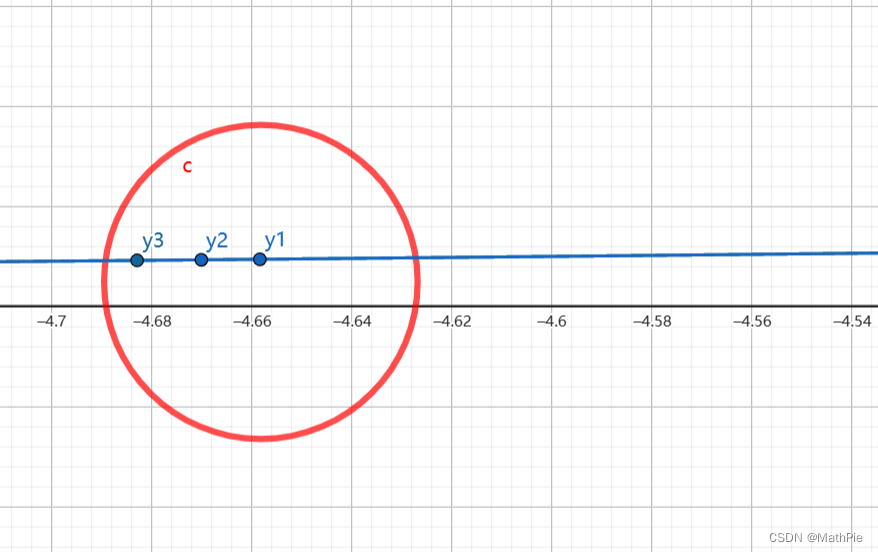
图2为$y=e^x$放大图，红圈圈住的部分是任意一段函数曲线，我们可以看到$y=e^x$在$x\to -\infty$时，$y\to 0$。用人话来说，$x\to -\infty$，就是x在一直变小，这个过程是无止境的，$y\to 0$就是y在无限逼近0，但取不到0
(这里的$y=e^x$本身便取不到0，但即使换一个函数比如说$y=sinx$，在$x\to 0$时，$y\to 0$，且$x=0$时，$y=0$，对于这种函数，我们要记得在$x=x_0$与$x\to x_0$这个过程没有关系，因为逼近终点的趋势与终点实际情况无关)

图2

那么在$y\to 0$时，如图2，y与x轴之间肯定可以有空隙(如图)，也就是肯定可以插入无穷多个点，或者说无穷多个f(x)（其实也就是在任何一个x处观察，函数可以继续向$x\to -\infty$延伸顺着蓝色的曲线，永无止境，如图3）

图3

而这用一句话来说就是函数f(x)在逼近极限值时，永远无法到达极限值，和极限值之间可以插入更接近极限的函数值这可以称为任一函数值与极限值之间存在空隙性质，这自然可以推广到任一有极限的函数与数列，也就是说任何有极限的函数或数列都存在这个性质

这个性质其实就是所谓保号性的第一条：由极限值函数值保号f(x)

其实第一条大家应该都易理解，重点在于第二条不好理解，尤其是加不加等号的问题

第二条

第一种解释:

如果函数f(x)是大于等于0的,那么当x趋近于x0时的极限设为A,因为A一定是f(x)的一个函数值那么A也必然大于等于0

第二种解释：

定义拆解：
1.$如果存在N>0,当n>N$时
这一点很好理解，就是形容函数值逼近极限的过程

2.$f(x)\ge 0(或f(x)\le 0)$时，$则A\ge 0(或A\le 0)$

由于函数值逼近极限只能是|A-f(x)|越来越小，所以$f(x)\ge 0$对应三种情况:

• 1.某个区间内只能恒等于0
• 2.一直大于0
• 3.在$n=N+1$时$f(x_n)=0$，$n>N+1$后便一直大于0($即f(x_n)若不恒等于0，就只能在一点处等于0$)(这里用的是n而不是$\delta$是为了方便说明)

所以，此时极限对应的三种情况:

• 1.当函数值在某个区间内只能恒等于0时，A=0
• 2.当函数值一直大于0时，$A\ge 0$
• 3.函数值在$n=N+1$时$f(x_n)=0$，$n>N+1$后便一直大于0时，$A\ge 0$
• 2与3其实就是一种情况，所以只剩两种情况，即在去心邻域内$f(x)>0$ 但这里之所以写出3是想说明不存在0与大于0两种函数值穿插的可能性，因为|A-f(x)|越来越小

这里进行解释：

（图4-图6的坐标横轴表示函数值f(x)而非自变量x）:

图4

第一种形式如图4，函数值可能从两侧逼近极限
此时函数值若大于0，则极限应大于0

图5

第二种形式如图5，函数值可能从比极限小的一侧逼近极限，
此时函数值大于0，极限值也大于0

图6

第三种形式如图6，函数值可能从比极限大的一侧逼近极限，此时函数值都大于0，
极限应为大于等于0，因为函数值无穷小时也大于0，但是极限对应为0