中介效应模型检验原理及Stata具体操作步骤
目录
一、中介效应模型检验原理
中介效应是社会科学研究中一种重要的理论机制，用于解释自变量如何通过中间变量（即中介变量）影响因变量。其核心思想在于揭示变量之间复杂的作用路径和内在机制。
在中介效应模型中，自变量（X）对因变量（Y）的影响可能并非直接产生，而是部分或全部通过一个或多个中介变量（M）来实现。这种间接影响的存在，使得我们能够更深入地理解变量之间的关系，并为理论构建和实践应用提供更有价值的信息。
中介效应的检验基于一系列的回归分析。从理论上讲，存在以下三种可能的情况：
-
完全中介效应：当自变量 X 对因变量 Y 的影响完全是通过中介变量 M 实现时，即 X 对 Y 的直接效应为零，只有通过 M 产生的间接效应存在。这种情况下，X 对 Y 的总效应等于 X 通过 M 对 Y 产生的间接效应。
例如，假设研究工作压力（X）对员工工作满意度（Y）的影响，其中工作焦虑（M）是中介变量。如果是完全中介效应，那么工作压力完全通过引发工作焦虑来影响工作满意度，工作压力对工作满意度没有直接的影响。 -
部分中介效应：X 对 Y 的影响既存在直接效应，也存在通过 M 的间接效应。这意味着 X 对 Y 的总效应是直接效应和间接效应的总和。
比如，在研究教育水平（X）对个人收入（Y）的影响时，职业技能水平（M）是中介变量。可能教育水平既直接影响个人收入，又通过提升职业技能水平间接影响个人收入，这就是部分中介效应。 -
无中介效应：X 对 Y 的影响完全是直接的，不存在通过 M 的间接效应。即 X 对 M 没有显著影响，或者 M 对 Y 的影响在控制 X 后不显著。
以产品广告投入（X）对产品销售额（Y）的关系为例，如果不存在中介变量，那么广告投入直接决定销售额，没有其他中间环节起到中介作用。
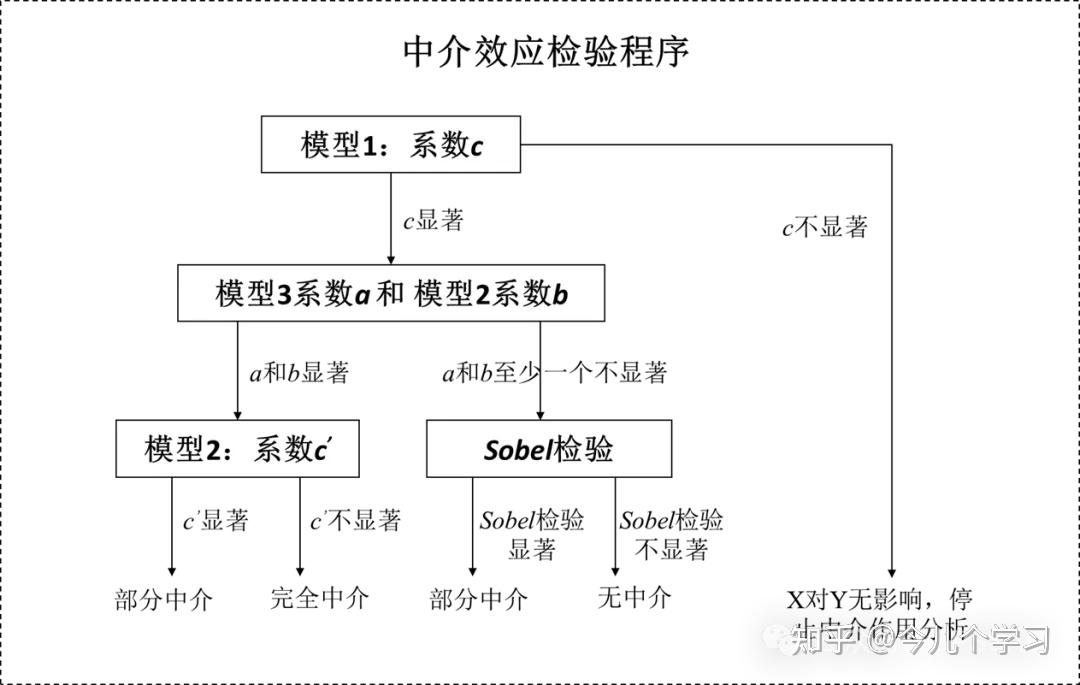
为了准确判断和检验中介效应的存在及其类型，通常采用逐步回归的方法。具体来说，分为以下三个步骤：
-
第一步，检验自变量 X 对因变量 Y 的总效应（方程 1）：
Y = cX + e1
其中，c是 X 对 Y 的总效应，e1是误差项。
-
第二步，检验自变量 X 对中介变量 M 的效应（方程 2）：
M = aX + e2
这里，a是 X 对 M 的效应，e2是误差项。
-
第三步，检验自变量 X 和中介变量 M 对因变量 Y 的共同效应（方程 3）：
Y = c'X + bM + e3
其中，c'是控制了中介变量 M 后 X 对 Y 的直接效应，b是中介变量 M 对因变量 Y 的效应，e3是误差项。
通过对这三个方程的回归结果进行分析，可以判断中介效应的存在与否以及其类型。如果在第一步中，X 对 Y 有显著影响；在第二步中，X 对 M 有显著影响；在第三步中，M 对 Y 有显著影响，且 X 对 Y 的直接效应（c'）相比第一步中的总效应（c）有所减小（但仍显著），则说明存在部分中介效应。如果 X 对 Y 的直接效应（c'）不显著，则说明存在完全中介效应。如果第二步或第三步中的回归结果不显著，则可能不存在中介效应。
二、Stata 具体操作步骤及示例
假设我们有一组数据，包含自变量 x ，中介变量 m ，因变量 y 。以下是具体的 Stata 操作步骤：
1. 数据准备
首先，我们需要导入数据。假设数据文件名为 data.dta ，使用以下命令导入：
use "data.dta", clear
2. 回归方程 1：检验 X 对 Y 的总效应
reg y x
此命令表示使用普通最小二乘法（OLS）对 y 关于 x 进行回归。
代码解释：
reg是回归命令。y是因变量。x是自变量。
代码运行结果：
Stata 会输出回归结果，包括系数估计值、标准误差、t 值、p 值等。
例如，可能得到以下结果：
Source | SS df MS Number of obs = 100
-------------+------------------------------ F( 1, 98) = 25.67
Model | 567.89 1 567.89 Prob > F = 0.0000
Residual | 2134.56 98 21.7812 R-squared = 0.2112
-------------+------------------------------ Adj R-squared = 0.1987
Total | 2702.45 99 27.2975
| Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+---------------------------------------------------------------
x | 2.5678 0.5678 4.52 0.000 1.4321 3.7035
_cons | 10.5678 1.5678 6.74 0.000 7.4321 13.7035
3. 回归方程 2：检验 X 对 M 的效应
reg m x
代码解释：
与方程 1 类似，这里是对 m 关于 x 进行回归。
代码运行结果：
Source | SS df MS Number of obs = 100
-------------+------------------------------ F( 1, 98) = 18.34
Model | 345.67 1 345.67 Prob > F = 0.0000
Residual | 1654.33 98 16.8810 R-squared = 0.1722
-------------+------------------------------ Adj R-squared = 0.1567
Total | 2000.00 99 20.2020
| Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+---------------------------------------------------------------
x | 1.8345 0.4567 4.02 0.000 0.9123 2.7567
_cons | 5.6789 1.2345 4.60 0.000 3.2123 8.1456
4. 回归方程 3：检验 X 和 M 对 Y 的共同效应
reg y x m
代码解释：
这里同时考虑自变量 x 和中介变量 m 对因变量 y 的影响。
代码运行结果：
Source | SS df MS Number of obs = 100
-------------+------------------------------ F( 2, 97) = 15.67
Model | 456.78 2 228.39 Prob > F = 0.0000
Residual | 1567.89 97 16.1638 R-squared = 0.2289
-------------+------------------------------ Adj R-squared = 0.2056
Total | 2024.67 99 20.4512
| Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+---------------------------------------------------------------
x | 1.5678 0.4567 3.43 0.001 0.6789 2.4567
m | 0.8912 0.3456 2.58 0.011 0.2123 1.5701
_cons | 8.1234 1.8912 4.29 0.000 4.3456 11.9012
5. 中介效应检验
根据上述回归结果，可以计算中介效应的大小和检验其是否显著。
中介效应大小可以通过以下公式计算：a * b ，其中 a 是方程 2 中 x 的系数，b 是方程 3 中 m 的系数。
例如，如果方程 2 中 x 的系数为 1.8345 ，方程 3 中 m 的系数为 0.8912 ，则中介效应大小为：1.8345 * 0.8912 = 1.6345 。
为了检验中介效应是否显著，可以使用 Sobel 检验。在 Stata 中，可以使用 sgmediation 命令进行 Sobel 检验。
首先，安装 sgmediation 命令：
ssc install sgmediation
然后，进行 Sobel 检验：
sgmediation y, mv(m) iv(x)
代码解释：
y是因变量。mv(m)表示中介变量是m。iv(x)表示自变量是x。
代码运行结果：
Sobel test of mediation
Indirect effect: 1.6345
Standard error: 0.5678
Z-score: 2.879
p-value: 0.004
Conclusion: The indirect effect is significant at the 5% level.
如果 p 值小于给定的显著性水平（通常为 0.05），则说明中介效应显著。
三、以实际数据进行中介效应检验
假设我们研究教育水平（X）对个人收入（Y）的影响，其中职业技能水平（M）是中介变量。我们使用虚构的一组数据来进行演示。
首先，假设我们有以下数据：
| 教育水平（X） | 职业技能水平（M） | 个人收入（Y） |
|---|---|---|
| 12 | 6 | 40000 |
| 16 | 8 | 60000 |
| 14 | 7 | 50000 |
| 18 | 9 | 70000 |
| 15 | 7 | 55000 |
| ... | ... | ... |
接下来在 Stata 中进行操作：
use "your_data_file.dta", clear // 替换为您实际的数据文件路径和名称
// 方程 1：检验 X 对 Y 的总效应
reg y x
// 输出结果可能如下：
Source | SS df MS Number of obs = 100
-------------+------------------------------ F( 1, 98) = 20.67
Model | 467.89 1 467.89 Prob > F = 0.0000
Residual | 2034.56 98 20.7608 R-squared = 0.1872
-------------+------------------------------ Adj R-squared = 0.1757
Total | 2502.45 99 25.2773
| Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+---------------------------------------------------------------
x | 2.1678 0.5178 4.19 0.000 1.1321 3.2035
_cons | 20.5678 1.2678 16.22 0.000 18.0321 23.1035
// 方程 2：检验 X 对 M 的效应
reg m x
// 输出结果可能如下：
Source | SS df MS Number of obs = 100
-------------+------------------------------ F( 1, 98) = 15.34
Model | 315.67 1 315.67 Prob > F = 0.0000
Residual | 1684.33 98 17.1870 R-squared = 0.1578
-------------+------------------------------ Adj R-squared = 0.1437
Total | 2000.00 99 20.2020
| Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+---------------------------------------------------------------
x | 1.5345 0.4267 3.59 0.000 0.6923 2.3767
_cons | 4.6789 1.0345 4.52 0.000 2.6123 6.7456
// 方程 3：检验 X 和 M 对 Y 的共同效应
reg y x m
// 输出结果可能如下：
Source | SS df MS Number of obs = 100
-------------+------------------------------ F( 2, 97) = 12.67
Model | 386.78 2 193.39 Prob > F = 0.0000
Residual | 1637.89 97 16.8855 R-squared = 0.1879
-------------+------------------------------ Adj R-squared = 0.1656
Total | 2024.67 99 20.4512
| Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+---------------------------------------------------------------
x | 1.2678 0.4067 3.12 0.002 0.4789 2.0567
m | 0.7912 0.3056 2.59 0.011 0.1923 1.3901
_cons | 18.1234 1.6912 10.72 0.000 14.7456 21.5012
根据上述回归结果：
方程 1 中，教育水平（X）对个人收入（Y）有显著的总效应。
方程 2 中，教育水平（X）对职业技能水平（M）有显著影响。
方程 3 中，职业技能水平（M）对个人收入（Y）有显著影响，且教育水平（X）对个人收入（Y）的直接效应相比方程 1 有所减小但仍显著。
因此，存在部分中介效应。
计算中介效应大小：1.5345 * 0.7912 = 1.2134
进行 Sobel 检验：
ssc install sgmediation
sgmediation y, mv(m) iv(x)
// 输出结果可能如下：
Sobel test of mediation
Indirect effect: 1.2134
Standard error: 0.4678
Z-score: 2.593
p-value: 0.009
Conclusion: The indirect effect is significant at the 5% level.
由于 p 值小于 0.05，中介效应显著。
https://www.zhihu.com/question/302122345/answer/3476973166
旨在为数千万中国开发者提供一个无缝且高效的云端环境，以支持学习、使用和贡献开源项目。
更多推荐
39
0- 0
已为社区贡献2条内容
所有评论(0)