史上最全pytorch学习笔记1【附有源代码和参考书籍】
在PyTorch中, torch.Tensor 是存储和变换数据的主要⼯具。如果你之前⽤过NumPy,你会发现Tensor 和NumPy的多维数组⾮常类似。然⽽, Tensor 提供GPU计算和⾃动求梯度等更多功能,这些使 Tensor 更加适合深度学习。
1. 数据操作
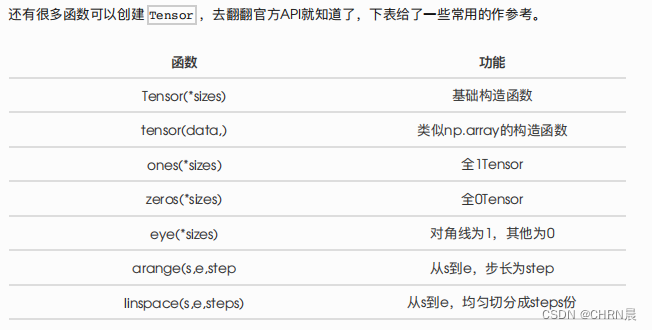
先介绍 Tensor 的最基本功能,即 Tensor 的创建。
1.1 创建tensor
#导入Pytorch
import torch
#创建5*3的未初始化的tensor
x = torch.empty(5, 3)
print(x)
tensor([[ 0.0000e+00, 1.5846e+29, 0.0000e+00],
[ 1.5846e+29, 5.6052e-45, 0.0000e+00],
[ 0.0000e+00, 0.0000e+00, 0.0000e+00],
[ 0.0000e+00, 0.0000e+00, 0.0000e+00],
[ 0.0000e+00, 1.5846e+29, -2.4336e+02]])
#创建⼀个5x3的随机初始化的 Tensor
x = torch.rand(5, 3)
print(x)
tensor([[0.4963, 0.7682, 0.0885],
[0.1320, 0.3074, 0.6341],
[0.4901, 0.8964, 0.4556],
[0.6323, 0.3489, 0.4017],
[0.0223, 0.1689, 0.2939]])
通过 shape 或者 size() 来获取 Tensor 的形状:
print(x.size())
print(x.shape)

1.2操作

#索引
y = x[0, :]
y += 1
print(y)
print(x[0, :]) # 源tensor也被改了
#⽤ view() 来改变 Tensor 的形状
y = x.view(15)
z = x.view(-1, 5) # -1所指的维度可以根据其他维度的值推出来
print(x.size(), y.size(), z.size())
torch.Size([5, 3]) torch.Size([15]) torch.Size([3, 5])

1.3广播机制
当对两个形状不同的 Tensor 按元素运算
时,可能会触发⼴播(broadcasting)机制:先适当复制元素使这两个 Tensor 形状相同后再按元素
运算。
x = torch.arange(1, 3).view(1, 2)
print(x)
y = torch.arange(1, 4).view(3, 1)
print(y)
print(x + y)
tensor([[1, 2]])
tensor([[1],
[2],
[3]])
tensor([[2, 3],
[3, 4],
[4, 5]])
1
2
3
4
5
6
7
1.4TENSOR 和NUMPY相互转换
我们很容易⽤ numpy() 和 from_numpy() 将 Tensor 和NumPy中的数组相互转换。但是需要注意的⼀
点是: 这两个函数所产⽣的的 Tensor 和NumPy中的数组共享相同的内存(所以他们之间的转换很
快),改变其中⼀个时另⼀个也会改变
#numpy()将tensor转为numpy数组
a=torch.ones(5)
b=a.numpy()
print(a,b)
a += 1
print(a, b)
b += 1
print(a, b)
tensor([1., 1., 1., 1., 1.]) [1. 1. 1. 1. 1.]
tensor([2., 2., 2., 2., 2.]) [2. 2. 2. 2. 2.]
tensor([3., 3., 3., 3., 3.]) [3. 3. 3. 3. 3.]
#使⽤ from_numpy() 将NumPy数组转换成 Tensor
import numpy as np
a = np.ones(5)
b = torch.from_numpy(a)
print(a, b)
a += 1
print(a, b)
b += 1
print(a, b)
[1. 1. 1. 1. 1.] tensor([1., 1., 1., 1., 1.], dtype=torch.float64)
[2. 2. 2. 2. 2.] tensor([2., 2., 2., 2., 2.], dtype=torch.float64)
[3. 3. 3. 3. 3.] tensor([3., 3., 3., 3., 3.], dtype=torch.float64)
#⽤⽅法 to() 可以将 Tensor 在CPU和GPU(需要硬件⽀持)之间相互移动。
if torch.cuda.is_available():
device=torch.device("cuda")
y = torch.ones_like(x, device=device) # 直接创建⼀个在GPU上的
Tensor
x = x.to(device) # 等价于 .to("cuda")
z = x + y
print(z)
print(z.to("cpu", torch.double)) # to()还可以同时更改数据类型
2.自动求梯度
在深度学习中,我们经常需要对函数求梯度(gradient)。PyTorch提供的autograd 包能够根据输⼊和前向传播过程⾃动构建计算图,并执⾏反向传播。
上⼀节介绍的 Tensor 是这个包的核⼼类,如果将其属性 .requires_grad 设置为 True ,它将开始追踪(track)在其上的所有操作(这样就可以利⽤链式法则进⾏梯度传播了)。完成计算后,可以调⽤ .backward() 来完成所有梯度计算。此 Tensor 的梯度将累积到 .grad 属性中。如果不想要被继续追踪,可以调⽤ .detach() 将其从追踪记录中分离出来,这样就可以防⽌将来的计算被追踪,这样梯度就传不过去了。此外,还可以⽤ with torch.no_grad() 将不想被追踪的操作代码块包裹起来,这种⽅法在评估模型的时候很常⽤,因为在评估模型时,我们并不需要计算可训练参数( requires_grad=True )的梯度。
Function 是另外⼀个很重要的类。 Tensor 和 Function 互相结合就可以构建⼀个记录有整个计算过程的有向⽆环图(DAG)。每个 Tensor 都有⼀个 .grad_fn 属性,该属性即创建该 Tensor 的Function , 就是说该 Tensor 是不是通过某些运算得到的,若是,则 grad_fn 返回⼀个与这些运算相关的对象,否则是None。
#创建⼀个 Tensor 并设置 requires_grad=True :
x = torch.ones(2, 2, requires_grad=True)
print(x)
print(x.grad_fn)
`
tensor([[1., 1.],
[1., 1.]], requires_grad=True)
None
`
y = x + 2
print(y)
print(y.grad_fn)
tensor([[3., 3.],
[3., 3.]], grad_fn=<AddBackward>)
<AddBackward object at 0x1100477b8>
'''注意x是直接创建的,所以它没有 grad_fn , ⽽y是通过⼀个加法操作创建的,所以它有⼀个为
<AddBackward> 的 grad_fn 。'''
z = y * y * 3
out = z.mean()
print(z, out)
'''tensor([[27., 27.],
[27., 27.]], grad_fn=<MulBackward>) tensor(27., grad_fn=
<MeanBackward1>)'''
#因为 out 是⼀个标量,所以调⽤ backward() 时不需要指定求导变量:
out.backward() # 等价于 out.backward(torch.tensor(1.))grad在反向传播过程中是累加的(accumulated),这意味着每⼀次运⾏反向传播,梯度都会累加之前的梯度,所以⼀般在反向传播之前需把梯度清零
#再来反向传播⼀次,注意grad是累加的
out2 = x.sum()
out2.backward()
print(x.grad)
out3 = x.sum()
x.grad.data.zero_()
out3.backward()
print(x.grad)
tensor([[5.5000, 5.5000],
[5.5000, 5.5000]])
tensor([[1., 1.],
[1., 1.]])
3.线性回归
线性回归输出是⼀个连续值,因此适⽤于回归问题。回归问题在实际中很常⻅,如预测房屋价格、⽓温、销售额等连续值的问题。与回归问题不同,分类问题中模型的最终输出是⼀个离散值。我们所说的图像分类、垃圾邮件识别、疾病检测等输出为离散值的问题都属于分类问题的范畴。softmax回归则适⽤于分类问题。
由于线性回归和softmax回归都是单层神经⽹络,它们涉及的概念和技术同样适⽤于⼤多数的深度学习模型。我们⾸先以线性回归为例,介绍⼤多数深度学习模型的基本要素和表示⽅法。

%matplotlib inline
import torch
from IPython import display
from matplotlib import pyplot as plt
import numpy as np
import random
um_inputs = 2
num_examples = 1000
true_w = [2, -3.4]
true_b = 4.2
features = torch.from_numpy(np.random.normal(0, 1, (num_examples,
num_inputs)))
labels = true_w[0] * features[:, 0] + true_w[1] * features[:, 1] +
true_b
labels += torch.from_numpy(np.random.normal(0, 0.01,
size=labels.size()))
print(features[0], labels[0])
tensor([0.8557, 0.4793]) tensor(4.2887) 1
通过⽣成第⼆个特征 features[:, 1] 和标签 labels 的散点图,可以更直观地观察两者间的线性关
系。
plt.scatter(features[:, 1].numpy(), labels.numpy(), 1);

#读取数据需要遍历数据集并不断读取⼩批量数据样本。这⾥我们定义⼀个函数:它每次返回 batch_size (批量⼤⼩)个随机样本的特征和标签。
def data_iter(batch_size, features, labels):
num_examples = len(features)
indices = list(range(num_examples))
random.shuffle(indices) # 样本的读取顺序是随机的
for i in range(0, num_examples, batch_size):
j = torch.LongTensor(indices[i: min(i + batch_size,
num_examples)]) # 最后⼀次可能不⾜⼀个batch
yield features.index_select(0, j), labels.index_select(0,
j)
我们读取第⼀个⼩批量数据样本并打印。每个批量的特征形状为(10, 2),分别对应批量⼤⼩和输⼊个
数;标签形状为批量⼤⼩。
batch_size = 10
for X, y in data_iter(batch_size, features, labels):
print(X, y)
break
tensor([[-1.4239, -1.3788],
[ 0.0275, 1.3550],
[ 0.7616, -1.1384],
[ 0.2967, -0.1162],
[ 0.0822, 2.0826],
[-0.6343, -0.7222],
[ 0.4282, 0.0235],
[ 1.4056, 0.3506],
[-0.6496, -0.5202],
[-0.3969, -0.9951]])
tensor([ 6.0394, -0.3365, 9.5882, 5.1810, -2.7355, 5.3873,
4.9827, 5.7962,
4.6727, 6.7921])
#初始化模型参数
#我们将权重初始化成均值为0、标准差为0.01的正态随机数,偏差则初始化成0。
w = torch.tensor(np.random.normal(0, 0.01, (num_inputs, 1)),
dtype=torch.float32)
b = torch.zeros(1, dtype=torch.float32)
#之后的模型训练中,需要对这些参数求梯度来迭代参数的值,因此我们要让它们的
#requires_grad=True 。
w.requires_grad_(requires_grad=True)
b.requires_grad_(requires_grad=True)
#定义模型
#下⾯是线性回归的⽮量计算表达式的实现。我们使⽤ mm 函数做矩阵乘法。
def linreg(x,w,b):
return torch.mm(x,w)+b
#定义损失函数
def squared_loss(y_hat,y):
return(y_hat-y.view(y_hat.size()))**2/2
#定义优化算法
'''以下的 sgd 函数实现了上⼀节中介绍的⼩批量随机梯度下降算法。它通过不断迭代模型参数来优化损失
函数。这⾥⾃动求梯度模块计算得来的梯度是⼀个批量样本的梯度和。我们将它除以批量⼤⼩来得到平
均值。'''
def sgd(params, lr, batch_size): # 本函数已保存在d2lzh_pytorch包中⽅便以后使⽤
for param in params:
param.data -= lr * param.grad / batch_size # 注意这⾥更改param时⽤的param.data
#训练模型
'''在训练中,我们将多次迭代模型参数。在每次迭代中,我们根据当前读取的⼩批量数据样本(特征 X 和
标签 y ),通过调⽤反向函数 backward 计算⼩批量随机梯度,并调⽤优化算法 sgd 迭代模型参数。
由于我们之前设批量⼤⼩ batch_size 为10,每个⼩批量的损失 l 的形状为(10, 1)。回忆⼀下⾃动求
梯度⼀节。由于变量 l 并不是⼀个标量,所以我们可以调⽤ .sum() 将其求和得到⼀个标量,再运
⾏ l.backward() 得到该变量有关模型参数的梯度。注意在每次更新完参数后不要忘了将参数的梯度清
零。
在⼀个迭代周期(epoch)中,我们将完整遍历⼀遍 data_iter 函数,并对训练数据集中所有样本都
使⽤⼀次(假设样本数能够被批量⼤⼩整除)。这⾥的迭代周期个数 num_epochs 和学习率 lr 都是超
参数,分别设3和0.03。在实践中,⼤多超参数都需要通过反复试错来不断调节。虽然迭代周期数设得
越⼤模型可能越有效,但是训练时间可能过⻓。⽽有关学习率对模型的影响,'''
lr = 0.03
num_epochs = 3
net = linreg
loss = squared_loss
for epoch in range(num_epochs): # 训练模型⼀共需要num_epochs个迭代周期
# 在每⼀个迭代周期中,会使⽤训练数据集中所有样本⼀次(假设样本数能够被批量⼤⼩整除)。X# 和y分别是⼩批量样本的特征和标签
for X, y in data_iter(batch_size, features, labels):
l = loss(net(X, w, b), y).sum() # l是有关⼩批量X和y的损失
l.backward() # ⼩批量的损失对模型参数求梯度
sgd([w, b], lr, batch_size) # 使⽤⼩批量随机梯度下降迭代模型参数
# 不要忘了梯度清零
w.grad.data.zero_()
b.grad.data.zero_()
train_l = loss(net(features, w, b), labels)
print('epoch %d, loss %f' % (epoch + 1, train_l.mean().item()))

#线性回归简洁实现
#features 是训练数据特征, labels 是标签。
num_inputs = 2
num_examples = 1000
true_w = [2, -3.4]
true_b = 4.2
features = torch.tensor(np.random.normal(0, 1, (num_examples,
num_inputs)), dtype=torch.float)
labels = true_w[0] * features[:, 0] + true_w[1] * features[:, 1] +
true_b
labels += torch.tensor(np.random.normal(0, 0.01,
size=labels.size()), dtype=torch.float)
'''PyTorch提供了 data 包来读取数据。由于 data 常⽤作变量名,我们将导⼊的 data 模块⽤ Data 代
替。在每⼀次迭代中,我们将随机读取包含10个数据样本的⼩批量。'''
import torch.utils.data as data
batch_size=10
#将训练数据特征与标签结合
dataset=data.TensorDataset(features,labels)
# 随机读取⼩批量
data_iter = Data.DataLoader(dataset, batch_size, shuffle=True)
for x,y in data_iter:
print(x,y)
break
tensor([[-2.7723, -0.6627],
[-1.1058, 0.7688],
[ 0.4901, -1.2260],
[-0.7227, -0.2664],
[-0.3390, 0.1162],
[ 1.6705, -2.7930],
[ 0.2576, -0.2928],
[ 2.0475, -2.7440],
[ 1.0685, 1.1920],
[ 1.0996, 0.5106]])
tensor([ 0.9066, -0.6247, 9.3383, 3.6537, 3.1283, 17.0213,
5.6953, 17.6279,
2.2809, 4.6661])
import torch
import numpy as np
import torch.nn as nn
num_inputs = 2
num_examples = 1000
true_w = [2, -3.4]
true_b = 4.2
features = torch.tensor(np.random.normal(0, 1, (num_examples,
num_inputs)), dtype=torch.float)
labels = true_w[0] * features[:, 0] + true_w[1] * features[:, 1] +
true_b
labels += torch.tensor(np.random.normal(0, 0.01,
size=labels.size()), dtype=torch.float)
import torch.utils.data as Data
batch_size = 10
# 将训练数据的特征和标签组合
dataset = Data.TensorDataset(features, labels)
# 随机读取⼩批量
data_iter = Data.DataLoader(dataset, batch_size, shuffle=True)
for X, y in data_iter:
print(X, y)
break
'''⾸先,导⼊ torch.nn 模块。实际上,“nn”是neural networks(神经⽹络)的缩写。顾名思义,该模
块定义了⼤量神经⽹络的层。之前我们已经⽤过了 autograd ,⽽ nn 就是利⽤ autograd 来定义模
型。 nn 的核⼼数据结构是 Module ,它是⼀个抽象概念,既可以表示神经⽹络中的某个层(layer),
也可以表示⼀个包含很多层的神经⽹络。在实际使⽤中,最常⻅的做法是继承 nn.Module ,撰写⾃⼰
的⽹络/层。⼀个 nn.Module 实例应该包含⼀些层以及返回输出的前向传播(forward)⽅法。下⾯先
来看看如何⽤ nn.Module 实现⼀个线性回归模型。'''
class LinearNet(nn.Module):
def __init(self,n_feature):
super(LinearNet,self).__init()
self.linear=nn.Linear(n_feature,1)
#forword定义前向传播
def forword(self,x):
y=self.linear(x);
return y
net=LinearNet(num_inputs)
print(net)
'''我们还可以⽤ nn.Sequential 来更加⽅便地搭建⽹络, Sequential 是⼀个有序的容器,⽹络
层将按照在传⼊ Sequential 的顺序依次被添加到计算图中。'''
# 写法⼀
net = nn.Sequential(
nn.Linear(num_inputs, 1)
# 此处还可以传⼊其他层
)
# 写法⼆
net = nn.Sequential()
net.add_module('linear', nn.Linear(num_inputs, 1))
# net.add_module ......
#查看所有的可学习参数
for param in net.parameters():
print(param)
#初始化模型参数,如线性回归模型中的权᯿和偏差。PyTorch在 init 模块中提供了多种参数初始化⽅法
from torch.nn import init
'''通过 init.normal_ 将
权᯿参数每个元素初始化为随机采样于均值为0、标准差为0.01的正态分布。偏差会初始化为零。'''
init.normal_(net[0].weight,mean=0,std=0.1)
init.constant_(net[0].bias, val=0) # 也可以直接修改bias的data:
#定义损失函数
loss=nn.MSELoss()
#定义优化算法
'''torch.optim 模块提供了很多常⽤的优化算法
⽐如SGD、Adam和RMSProp等。下⾯我们创建⼀个⽤于优化 net 所有参数的优化器实例,并指定学
习率为0.03的⼩批量随机梯度下降(SGD)为优化算法。'''
import torch.optim as optim
optimizer = optim.SGD(net.parameters(), lr=0.03)
print(optimizer)
# 调整学习率
for param_group in optimizer.param_groups:
param_group['lr'] *= 0.1 # 学习率为之前的0.1倍
'''在使⽤Gluon训练模型时,我们通过调⽤ optim
实例的
step
函数来迭代模型参数。按照⼩批量随机梯
度下降的定义,我们在
step
函数中指明批量⼤⼩,从⽽对批量中样本梯度求平均。'''
num_epochs=3
for epoch in range(1,num_epochs+1):
for x,y in data_iter:
output=net(x)
l=loss(output,y.view(-1,1))
optimizer.zero_grad()## 梯度清零,等价于net.zero_grad()
l.backward()
optimizer.step()
print('epoch %d, loss: %f' % (epoch, l.item()))
'''使⽤PyTorch可以更简洁地实现模型。
torch.utils.data 模块提供了有关数据处理的⼯具, torch.nn 模块定义了⼤量神经⽹络的
层, torch.nn.init 模块定义了各种初始化⽅法, torch.optim 模块提供了模型参数初始化
的各种⽅法。''''''
4.softmax回归
前⼏节介绍的线性回归模型适⽤于输出为连续值的情景。在另⼀类情景中,模型输出可以是⼀个像图像类别这样的离散值。对于这样的离散值预测问题,我们可以使⽤诸如softmax回归在内的分类模型。和线性回归不同,softmax回归的输出单元从⼀个变成了多个,且引⼊了softmax运算使输出更适合离散值的预测和训练。
在介绍softmax回归的实现前我们先引⼊⼀个多类图像分类数据集。它将在后⾯的章节中被多次使⽤,以⽅便我们观察⽐较算法之间在模型精度和计算效率上的区别。图像分类数据集中最常⽤的是⼿写数字识别数据集MNIST[1]。但⼤部分模型在MNIST上的分类精度都超过了95%。为了更直观地观察算法之间的差异,我们将使⽤⼀个图像内容更加复杂的数据集Fashion-MNIST[2](这个数据集也⽐较⼩,只有⼏⼗M,没有GPU的电脑也能吃得消)。
本节我们将使⽤torchvision包,它是服务于PyTorch深度学习框架的,主要⽤来构建计算机视觉模型。
torchvision主要由以下⼏部分构成:
- torchvision.datasets : ⼀些加载数据的函数及常⽤的数据集接⼝;
- torchvision.models : 包含常⽤的模型结构(含预训练模型),例如AlexNet、VGG、
ResNet等; - torchvision.transforms : 常⽤的图⽚变换,例如裁剪、旋转等;
- torchvision.utils : 其他的⼀些有⽤的⽅法。
import torch
import torchvision
import torchvision.transforms as transforms
import matplotlib.pyplot as plt
import time
import sys
sys.path.append("..") # 为了导⼊上层⽬录的d2lzh_pytorch
import d2lzh_pytorch as d2l
'''下⾯,我们通过torchvision的 torchvision.datasets 来下载这个数据集。第⼀次调⽤时会⾃动从⽹
上获取数据。我们通过参数 train 来指定获取训练数据集或测试数据集(testing data set)。测试数
据集也叫测试集(testing set),只⽤来评价模型的表现,并不⽤来训练模型。
另外我们还指定了参数 transform = transforms.ToTensor() 使所有数据转换为 Tensor ,如果不
进⾏转换则返回的是PIL图⽚。 transforms.ToTensor() 将尺⼨为 (H x W x C) 且数据位于[0, 255]的
PIL 图⽚或者数据类型为 np.uint8 的 NumPy 数组转换为尺⼨为 (C x H x W) 且数据类型
为 torch.float32 且位于[0.0, 1.0]的 Tensor 。'''
mnist_train =
torchvision.datasets.FashionMNIST(root='~/Datasets/FashionMNIST',
train=True, download=True, transform=transforms.ToTensor())
mnist_test =
torchvision.datasets.FashionMNIST(root='~/Datasets/FashionMNIST',
train=False, download=True, transform=transforms.ToTensor())
print(type(mnist_train))
print(len(mnist_train), len(mnist_test))
<class 'torchvision.datasets.mnist.FashionMNIST'>
60000 10000
feature, label = mnist_train[0]
print(feature.shape, label) # Channel x Height X Width
#输出:
'''torch.Size([1, 28, 28]) tensor(9)
变量 feature 对应⾼和宽均为28像素的图像。由于我们使⽤了 transforms.ToTensor() ,所以每个
像素的数值为[0.0, 1.0]的32位浮点数。需要注意的是, feature 的尺⼨是 (C x H x W) 的,⽽不是 (H
x W x C)。第⼀维是通道数,因为数据集中是灰度图像,所以通道数为1。后⾯两维分别是图像的⾼和
宽。
Fashion-MNIST中⼀共包括了10个类别,分别为t-shirt(T恤)、trouser(裤⼦)、pullover(套衫)、
dress(连⾐裙)、coat(外套)、sandal(凉鞋)、shirt(衬衫)、sneaker(运动鞋)、
bag(包)和ankle boot(短靴)。以下函数可以将数值标签转成相应的⽂本标签。'''
def get_fashion_mnist_labels(labels):
text_labels = ['t-shirt', 'trouser', 'pullover', 'dress','coat','sandal', 'shirt', 'sneaker', 'bag', 'ankleboot']
return [text_labels[int(i)] for i in labels]
#定义⼀个可以在⼀⾏⾥画出多张图像和对应标签的函数。
def show_fashion_mnist(images,labels):
figs=plt.subplot(1,len(images),figsize=(12,12))
for f,img,lbl in zip(figs,images,labels):
f.imshow(img.view((28,28)).numpy())
f.set_title(lbl)
f.axes.get_xaxis().set_visible(False)
f.axes.get_yaxis().set_visible(False)
plt.show()
x,y=[],[]
for i in range(10):
x.append(mnist_train[i][0]])
y.append(mnist_train[i][1]])
show_fashion_mnist(x, get_fashion_mnist_labels(y))

#softmax回归的简洁实现
import torch
from torch import nn
from torch.nn import init
import numpy as np
import sys
sys.path.append("..")
import d2lzh_pytorch as d2l
batch_size = 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)
#定义和初始化模型
'''softmax回归的输出层是⼀个全连接层,所以我们⽤⼀个线性模块就
可以了。因为前⾯我们数据返回的每个batch样本 x 的形状为(batch_size, 1, 28, 28), 所以我们要先
⽤ view() 将 x 的形状转换成(batch_size, 784)才送⼊全连接层。'''
num_inputs = 784
num_outputs = 10
class LinearNet(nn.Model):
def __init__(self,num_inputs,num_outputs):
super(LinearNet,self).__init__()
self.linear=nn.Linear(num_inputs,num_outputs)
def forward(self,x):# x shape: (batch, 1, 28, 28)
y=self.linear(x.view(x.shape[0],-1))
return y
net=LinearNet(num_inputs,num_outputs)
#SOFTMAX和交叉熵损失函数
loss = nn.CrossEntropyLoss()
optimizer = torch.optim.SGD(net.parameters(), lr=0.1)
num_epochs=5
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs,
batch_size, None, None, optimizer)
#输出
epoch 1, loss 0.0031, train acc 0.745, test acc 0.790
epoch 2, loss 0.0022, train acc 0.812, test acc 0.807
epoch 3, loss 0.0021, train acc 0.825, test acc 0.806
epoch 4, loss 0.0020, train acc 0.832, test acc 0.810
epoch 5, loss 0.0019, train acc 0.838, test acc 0.823
5.多层感知机










import torch
from torch import nn
from torch.nn import init
import numpy as np
import sys
sys.path.append("..")
import d2lzh_pytorch as d2l
'''和softmax回归唯⼀的不同在于,我们多加了⼀个全连接层作为隐藏层。它的隐藏单元个数为256,并
使⽤ReLU函数作为激活函数。'''
num_inputs, num_outputs, num_hiddens = 784, 10, 256
net = nn.Sequential(
d2l.FlattenLayer(),
nn.Linear(num_inputs, num_hiddens),
nn.ReLU(),
nn.Linear(num_hiddens, num_outputs),
)
for params in net.parameters():
init.normal_(params, mean=0, std=0.01)
batch_size = 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)
loss = torch.nn.CrossEntropyLoss()
optimizer = torch.optim.SGD(net.parameters(), lr=0.5)
num_epochs = 5
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs,
batch_size, None, None, optimizer)

6.房价预测实战
# 如果没有安装pandas,请取消下一行的注释
# !pip install pandas
%matplotlib inline
import numpy as np
import pandas as pd
import torch
from torch import nn
from d2l import torch as d2l
#使用pandas分别加载包含训练数据和测试数据的两个CSV文件。
train_data = pd.read_csv(download('kaggle_house_train'))
test_data = pd.read_csv(download('kaggle_house_test'))
'''训练数据集包括1460个样本,每个样本80个特征和1个标签, 而测试数据集包含1459个样本,每个样本80个特征。'''
print(train_data.shape)
print(test_data.shape)
print(train_data.iloc[0:4, [0, 1, 2, 3, -3, -2, -1]])

我们可以看到,在每个样本中,第一个特征是ID, 这有助于模型识别每个训练样本。 虽然这很方便,但它不携带任何用于预测的信息。 因此,在将数据提供给模型之前,我们将其从数据集中删除。
all_features = pd.concat((train_data.iloc[:, 1:-1], test_data.iloc[:, 1:]))

#数据预处理
numeric_features=all_features.dtypes[all_features.dtypes != 'object'].index
all_features[numeric_features] = all_features[numeric_features].apply(
lambda x: (x - x.mean()) / (x.std()))
# 在标准化数据之后,所有均值消失,因此我们可以将缺失值设置为0
all_features[numeric_features] = all_features[numeric_features].fillna(0)
接下来,我们处理离散值。 这包括诸如“MSZoning”之类的特征。 我们用独热编码替换它们, 方法与前面将多类别标签转换为向量的方式相同 (请参见 3.4.1节)。 例如,“MSZoning”包含值“RL”和“Rm”。 我们将创建两个新的指示器特征“MSZoning_RL”和“MSZoning_RM”,其值为0或1。 根据独热编码,如果“MSZoning”的原始值为“RL”, 则:“MSZoning_RL”为1,“MSZoning_RM”为0。 pandas软件包会自动为我们实现这一点。
# “Dummy_na=True”将“na”(缺失值)视为有效的特征值,并为其创建指示符特征
all_features = pd.get_dummies(all_features, dummy_na=True)
all_features.shape

n_train = train_data.shape[0]
train_features = torch.tensor(all_features[:n_train].values, dtype=torch.float32)
test_features = torch.tensor(all_features[n_train:].values, dtype=torch.float32)
train_labels = torch.tensor(
train_data.SalePrice.values.reshape(-1, 1), dtype=torch.float32)
动手学深度学习(李沐)源码获取和PDF:
动手学深度学习(李沐)的pytorch版本(包含代码和pdf链接:https://pan.baidu.com/s/17uEh4x_GbO0F67bzgQkhuQ
提取码:cgbq
更多推荐
 已为社区贡献1条内容
已为社区贡献1条内容








所有评论(0)