传统的数值方法在处理复杂问题时可能需要大量的计算资源和时间，而改良后的PINN可以通过更有效的算法减少计算成本，使得求解过程更加高效。 在写论文时，我们也可以通过改进PINN减少数据需求、加速模型收敛、提高预测准确性、增强可解释性，从而提高论文的质量和影响力。

今天我就来分享物理信息神经网络（PINN）的15种改良创新方案，包括2024年最新，每种方案涉及的PINN变体和来源文章也都整理了，贴上了开源代码方便同学们复现。

最新的方案已经帮大家分析好了创新点，写论文的同学可以借鉴学习，其他paper看文末

1.NAS-PINN: NEURAL ARCHITECTURE SEARCH-GUIDED PHYSICS-INFORMED NEURAL NETWORK FOR SOLVING PDES

方法：本文提出了一种神经架构搜索引导的方法NAS-PINN，用于自动搜索解决给定PDE的最佳神经架构。通过构建混合操作并引入掩码来实现不同形状张量的相加，将架构搜索问题放松为一个连续的双层优化问题。它可以在给定的搜索空间中搜索最合适的隐藏层数和每层神经元的数量，并构建给定问题的最佳神经架构。

创新点：

• 提出了一种新的神经架构搜索方法，称为NAS-PINN。通过构建混合操作和引入掩码来实现不同形状张量的相加，将架构搜索问题转化为一个连续的双层优化问题。该方法可以在给定的搜索空间中搜索最合适的隐藏层和每层神经元的数量，并构建适用于给定问题的最佳神经架构。

• 在PINN框架中引入了空间信息。通过使用数值微分（ND）替代自动微分（AD），成功地将空间信息引入模型中，确保模型得到的解符合物理定律。这一方法可以提高模型的准确性和可靠性。

2.GPT-PINN: Generative Pre-Trained Physics-Informed Neural Networks toward non-intrusive Meta-learning of parametric PDEs

方法：本文的主要目的是使用受经典和数学严谨的RBM技术启发的策略，显著缩小PINNs的规模，并加速使用PINNs解决参数化PDEs的过程。与RBM类似，所提出的求解器具有初始投资成本。然而，由于其边际成本比每个PINN求解的成本低几个数量级，它们能够在需要重复或实时解决PDE的问题中提供显著的计算节省。

创新点:

• 设计了具有定制激活函数的网络架构，这些激活函数是通过贪婪算法选择的参数值实例化的预训练PINNs。

• 提出了一种全新的元学习范式，即GPT-PINN，用于解决参数化系统中PINNs面临的训练成本和过度参数化的挑战。通过设计网络架构和特殊的激活函数，并将元网络的训练损失作为误差指标，本文证明了GPT-PINN可以在整个参数域内准确高效地生成代理PINNs。

• 借鉴了经典的RBM技术，采用策略来显著减小PINNs的规模，并加速使用PINNs求解参数化PDE的过程。

3.META-PINN: META LEARNING FOR IMPROVED NEURAL NETWORK WAVEFIELD SOLUTIONS

方法：本文提出了一种基于元学习的初始化方法，用于改进物理信息神经网络（PINNs）在地震波场解估计中的性能。该方法通过元学习训练一个通用的网络初始化模型，用于一组介质参数（即速度模型）。然后，将元训练的PINN模型作为新速度模型的初始模型，通过物理和正则化损失的联合约束来进行常规PINN训练。

创新点：

• 作者提出了一种基于元学习的新颖初始化方法，用于改进物理信息神经网络（PINNs）的性能。

• 作者利用元学习训练了一个通用的网络初始化模型，用于一系列介质参数（即速度模型），并将其作为新速度模型的PINN训练的初始模型。

• 作者提出了Meta-PINN算法，利用元学习算法学习任务级非线性映射关系，从而加速新速度模型的PINN训练的收敛速度并提高波场解的准确性。

4.PINN-TI: Physical Information embedded in Neural Networks for solving ordinary differential equations with Time-varying Inputs

方法：本文提出了一种PINN-TI模型和SSF算法，可以通过训练一次来解决不同初始值或边界条件和不同时变输入的常微分方程问题。该方法基于传统数值解法中将时变输入离散化的思想，同时在训练过程中将物理信息嵌入神经网络中。

创新点：

• PINN-TI模型和SSF算法：作者设计了一种PINN-TI网络结构和一种Step-by-Step Forward (SSF)算法。该模型和算法使得网络能够在一次训练后预测不同初始值或边界条件以及不同时间变化输入（包括分段函数）下的常微分方程结果。这种方法可以扩展解的时间域到更大范围。

• 将物理信息嵌入神经网络：作者的解决方案基于将时间变化输入离散化的传统数值解方法的思想，同时在训练过程中将物理信息嵌入神经网络。作者还提到，这种离散化思想可以与DeepONet和FNO相结合，并且是未来的主要研究方向。此外，作者还指出，将MLP扩展为CNN或RNN以适用于不同问题是一个重要的未来研究方向。

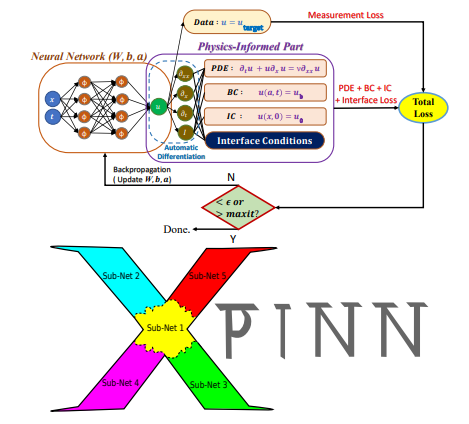
5.Extended physics-informed neural networks (XPINNs) : A generalized space-time domain decomposition based deep learning framework for nonlinear partial differential equations

方法：这篇论文介绍了一种名为Extended Physics-Informed Neural Networks (XPINN)的方法，用于解决复杂的高维方程系统。XPINN方法在分解的子域上应用了PINN方法，通过使用深度神经网络和残差点来实现准确的解。研究中使用了随机梯度下降（SGD）算法来最小化损失函数，并使用ADAM优化器进行训练。

创新点：

• 通过在共享边界上施加适当的连续性条件，将计算域分解为多个子域，并且这些子域仅通过共享边界相互交互。通过一系列独立子问题的解来恢复全局解。这种领域分解方法在标准数值方法（如有限元）中已经是一个基本的发展，用于在并行计算机上求解以PDE形式表示的物理定律。

• 在每个子域中使用单独的神经网络来求解问题，可以提高模型的表示能力。这意味着每个子域都可以使用适合其特定问题的网络结构和参数设置，从而提高模型的准确性和效率。

6.A Metalearning Approach for Physics-Informed Neural Networks (PINNs): Application to Parameterized PDEs

方法：本文通过研究应用于参数化PDEs的PINNs来解决优化挑战。作者通过元学习PINN的权重初始化，与以前的研究不同，使用了更准确的L-BFGS优化步骤，并且在测试时进行了更多的迭代次数，结果显示该方法在训练方案中表现更好且成本更低。

创新点：

• 使用模型感知方法成功地元学习了物理信息神经网络（PINNs）的权重初始化。通过在参数域的中心使用完全优化的PINN的初始化，利用参数化PDE在权重域中的平滑性，可以插值出最佳的权重初始化。

• 本文将PINNs的元学习应用于参数化PDEs，这是之前的研究所没有涉及到的。该方法不仅仅是替代现有文献的方法，而是对现有文献的补充。

7.Monte Carlo Neural PDE Solver for Learning PDEs via Probabilistic Representation

方法：本文提出了一种新的神经偏微分方程（PDE）求解器，称为MCNP Solver，它利用蒙特卡洛方法来训练神经网络求解器。该方法通过将宏观现象视为微观粒子的随机运动集合，构建了MCNP Solver的损失函数。为了提高MCNP Solver的性能和效率，文中提出了几种技巧，包括在对流过程中使用Heun方法来提高准确性，在扩散过程中利用邻近网格点的概率密度函数来近似数学期望。

创新点：

• MCNP Solver：提出了MCNP Solver，该方法利用费曼-卡克公式以无监督的方式训练神经PDE求解器。通过数值分析，证明了MCNP Solver在处理对流-扩散、Allen-Cahn和Navier-Stokes方程中的复杂时空变化和粗糙步长方面的能力。

• 插值技巧：在MCNP Solver中引入了插值技巧，以确保网格点的概率密度函数满足归一化条件。这种插值技巧在处理具有极低扩散率的情况下起到关键作用，可以减少相对误差，并且对于具有细步长的情况也可以减少局部随机步行的引入。

8.Physics-Informed Neural Operator for Learning Partial Differential Equations

方法：本文介绍了一种新的神经算子学习框架PINN (Physics-Informed Neural Network)，该框架结合了数据约束和PDE约束来解决逆问题。在实验中，作者使用PINN框架成功解决了Kolmogorov流、Burgers方程、Darcy流和Navier-Stokes方程等多个物理问题。此外，PINN框架还能够通过实例微调来进一步提高解决特定问题的能力。

创新点：

• PINO是第一个将数据和PDE约束结合在不同分辨率下学习算子的混合方法。

• PINO使用傅里叶神经算子（FNO）框架，该框架保证了对于任何连续算子都是一个通用逼近器，并在网格细化的极限下收敛。

• PINO在没有训练数据的情况下，仅通过PDE约束就可以成功解决问题，而之前的方法（如PINN）由于优化挑战而失败。

• PINO可以在超出训练数据分辨率的情况下准确预测，即零样本超分辨率。

• PINO可以解决逆问题，并通过PDE约束限制预测结果在物理有效的流形上。

• PINO可以在不同分辨率下结合数据和PDE约束进行训练，具有更高的准确性和更好的优化效果。

• PINO具有分辨率收敛的性质，可以在分辨率无限增加时逼近连续算子的极限。

• PINO可以在未见过的高频率上进行外推，而表示等价模型无法生成新的频率。

关注下方《学姐带你玩AI》🚀🚀🚀

回复“PINN改良”获取论文+代码

码字不易，欢迎大家点赞评论收藏