系列文章目录： MODIS数据处理

---

一、说明

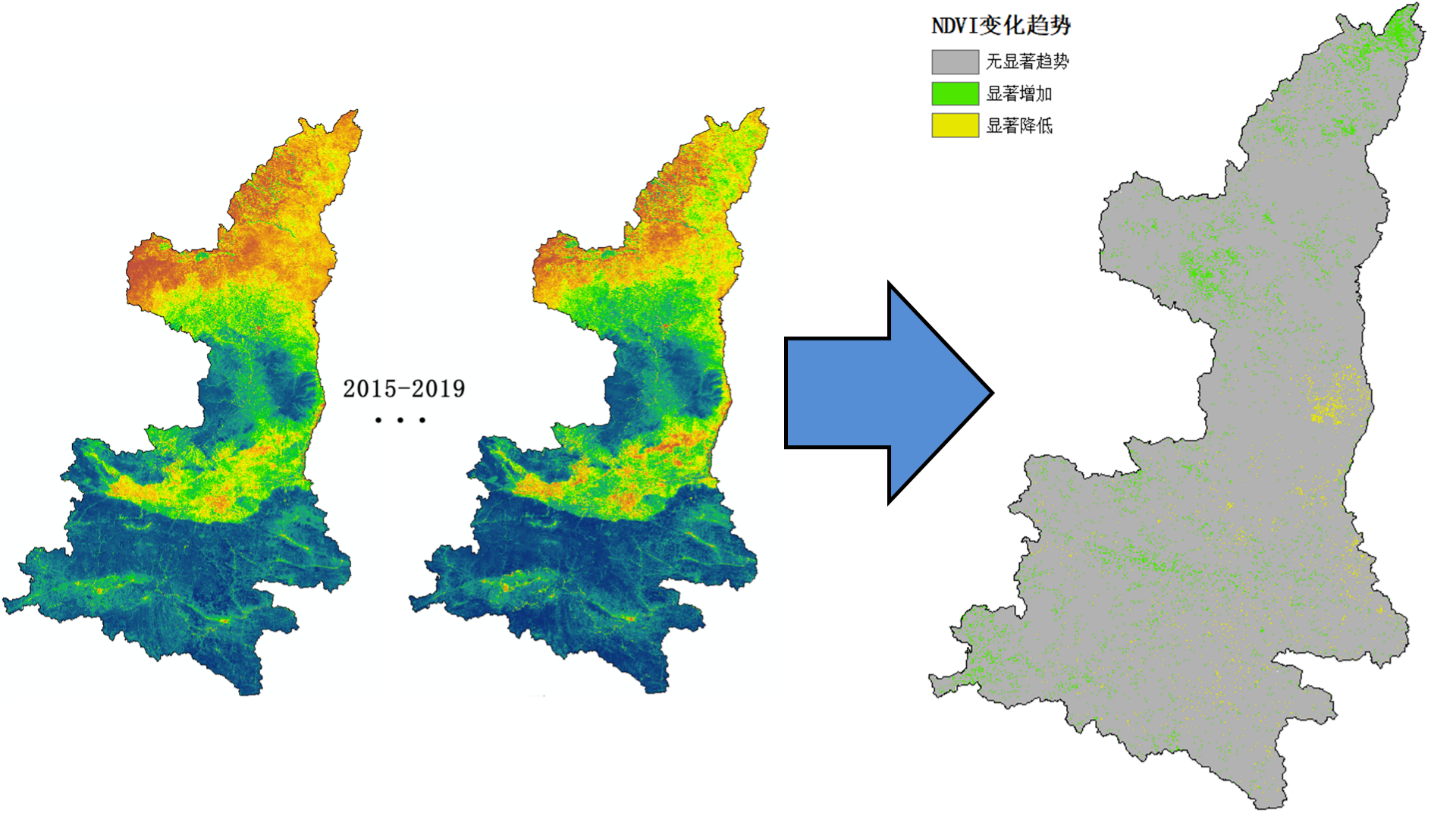
以分析陕西省近5年7月份的NDVI变化趋势为例，变化趋势的用线性回归的斜率和显著性来表示，参考文献间：
[1]元志辉,包刚,银山,雷军,包玉海,萨楚拉.2000-2014年浑善达克沙地植被覆盖变化研究[J].草业学报,2016,25(01):33-46.
[2]贾艳红,赵传燕,南忠仁.西北干旱区黑河下游植被覆盖变化研究综述[J].地理科学进展,2007(04):64-74.
可以简单理解为在某位置(x,y)2015~2019年的逐年NDVI值构成的一个长度为5的时间序列，用一元线性回归拟合这个序列，并用斜率slope来反映该处NDVI的变化趋势。这部分可以参考贾俊平的统计学(第六版)第9章关于一元线性回归模型的估计和检验的说明。

---

二、操作步骤

注：需要利用ArcGIS和python，需要用到的代码见下文，python需要安装依赖库(scipy、numpy、pandas)。

2.1 处理NDVI数据

处理过程可以参考添加链接描述，我这边准备了近5年的NDVI栅格数据，分辨率为250m。
注意：要保证各年的NDVI栅格的分辨率和坐标系是相同的，这里我用的坐标系是WGS_1984_UTM_Zone_49N

2.2 栅格转点

2.3 多值提取至点

这一步的耗时可能较长

运行结束后打开输入点要素的属性表可以看到匹配好的点对

2.4 添加经纬度坐标

工具箱\系统工具箱\data management tools.tbx\要素\添加 xy 坐标

运行结束后，要素的属性表会多出来两列，分别对应x、y坐标，由于我用的是UTM分带投影坐标系，单位是m。

下面将改属性表导出为txt文件

---

2.5 利用python计算斜率和显著性系数

import pandas as pd
import scipy.stats as stats
"""
读取存储有多年NDVI信息的表格，对于位置[x,y]来说有NDVI构成的时间序列
如：[NDVI_2015,NDVI_2016,NDVI_2017,NDVI_2018,NDVI_2019]
用一元线性回归分析这个时间序列的趋势和显著性

输入
txt_file:str
    待分析的表格的完整路径
vi_names:List[str]
    NDVI时间序列对应的列名组成列表,如['2015', '2016', '2017', '2018', '2019']
out_file:str
    斜率和显著性系数结果的输出路径
"""
# 输入
txt_file = r"E:\GIS教程\趋势分析\shanxi15-19.txt"
vi_names = ['2015', '2016', '2017', '2018', '2019']
out_file = r"E:\GIS教程\趋势分析\slope and alpha.csv"

vi_years = pd.read_table(txt_file, sep=",",thousands=",")
virows = vi_years[vi_names].values
years = range(len(vi_names))
slopes = []
alphas = []
for virow in virows:
    slope, itc, r, p, *useless = stats.linregress(years,virow)
    slopes.append(slope)
    alphas.append(p)
vi_years.insert(len(vi_years.columns), "slope", slopes)
vi_years.insert(len(vi_years.columns), "alpha", alphas)
vi_years[["POINT_X","POINT_Y","slope","alpha"]].to_csv(out_file)

2.6 转为栅格

• 导入表格文件到csv
  
• 显示XY数据，注意要和栅格的坐标系设置为一致
  
  
• 保存得到的点要素
  
  
• 用点转栅格工具分别将要素的slope和alpha字段转为栅格，参数设置中需要将像元大小和原始的NDVI栅格大小保持一致
  
  至此我们就得到了斜率和显著性系数的栅格影像。
  

三、变化趋势分级

可以按照斜率slope和显著性系数alpha的大小将多年NDVI的变化趋势分为以下三类：

1. alpha >=0.05;无显著变化,用数字1表示
2. slope>0,alpha<0.05;显著增加,用数字2表示
3. slope<0,alpha<0.05;显著降低,用数字3表示

用栅格计算器完成分级操作，地图代数表达式为：

Con("alpha.tif">=0.05,1,Con("slope.tif">0,2,3))

---