【算法】【欧几里得】数据结构与算法之欧几里得算法详解(附完整代码)
前言:
完整代码在附录在末尾
一、什么是欧几里得算法
欧几里得算法(又称辗转相除法)用于计算两个数的最大公约数,被称为世界上最古老的 算法。现在人们已无法确定该算法具体的提出时间,但其最早被发现记载于公元前 300 年欧几 里得的著作中,因此得以命名。
二、欧几里得算法的实现过程
通常的做法是先对两个数字因式分解,找出共同的素数,然后求出最大公约数(GCD)。这样就能求出 两个数的最大公约数为多少。然而两个数字越大,因式分解就越难。此时,使用欧几里得算法就 能更高效地求解最大公约数。
什么是最大公约数(指两个或多个整数共有约数中最大的一个。)
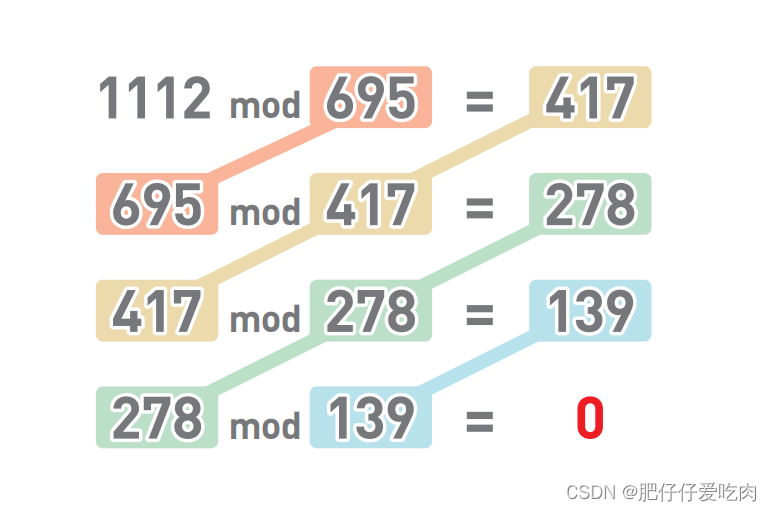
我们以1112与695这两个数的最大公约数为例:
1.首先用较小的数字去除较大的数字,求出余 数。也就是对两个数字进行 mod 运算。除完后的余数为417。

2.接下来再用除数695和余数417进行mod运 算。结果为278。

3.继续重复同样的操作,对417和278进行mod 运算,结果为139。

4.对278和139进行mod运算,结果为0。也就 是说,278可以被139整除。

5.余数为0时,最后一次运算中的除数139就是 1112和695的最大公约数。

三、欧几里得算法的分析
1.为什么用欧几里得算法可以求得最大公约数 呢?我们结合图片来想一想。

2. 将最大公约数设为n,然后在直线上画出相应刻度。由于我们已知最大公约数为 139,所以为了方便理 解,在1112上画出8个刻度,在695上画出5个刻度。

3.这里和前面的运算一样,用小的数去除大的数,得到的余数为417。

4.继续重复mod运算。用417去除695,得到余数278。

5.继续做除法。由于278可以被 139整除,所 以……

6.余数为0。此时便能求得最大公约数n为139。

四、总结
使用欧几里得算法,只需重复做除法便能求得最大公约数。这个算法最大的优势就 在于即使两个数字再大,只要按照步骤进行操作就能高效地求得两者的最大公约数。
附录1:一般方式实现(C语言实现)
#include <stdio.h>
int main()
{
int data1, data2;
int data;
scanf_s("%d%d", &data1, &data2);
if (data1 > 0 && data2 > 0)//判断数据合法
{
if (data1 > data2)//将两个数据大小位置固定
{
int temp = data1;
data1 = data2;
data2 = temp;
}
data = data1 % data2;
while (data)
{
data1 = data2;
data2 = data;
data = data1 % data2;
}
printf("%d\n", data2);//最后结果保存在data2中
}
return 0;
}附录2:递归方式实现
#include<stdio.h>
int rec(int data1, int data2)
{
int data, temp;
data = data1 % data2;
if (data == 0)
return data2;//最后结果保存在data2中
else
rec(data2, data);
}
int main()
{
int data1, data2;
int data;
scanf("%d%d", &data1, &data2);
if (data1 > 0 && data2 > 0)
{
if (data1 > data2)//将两个数据大小位置固定
{
int temp = data1;
data1 = data2;
data2 = temp;
}
printf("%d\n", rec(data1, data2));
}
return 0;
}参考书籍《我的第一本算法书》
更多推荐
 已为社区贡献11条内容
已为社区贡献11条内容









所有评论(0)