我的个人博客文章链接如下：学习通信原理之——彻底理解频谱和频谱密度

前言

最近还是在复习通信原理，但是对于频谱/频谱密度/能量谱/能量谱密度/功率谱/功率谱密度还是一知半解的，所以我就去各种看资料，看视频，又去问了问老师。
所以我在这里写下自己对这两个概念的一些分析和理解，不敢说100%正确，仅供大家参考。

频谱

频谱的定义

书上的说法是

以频率为坐标，分别以幅值、相位为纵坐标得到的图就是频谱。其中以幅值为纵坐标的图称为幅度谱，以相位为纵坐标的称为相位谱。

我感觉最通俗的解释就是信号的某种特征量随信号频率的关系，称为频谱

符号定义

接下来文中出现的符号定义

符号	含义
$$T$$	信号周期
$$\Omega$$	频域信号两个谱线之间的间距
$$\tau$$	时域信号宽度

周期信号

周期信号的傅立叶级数具有幅频特性和相频特性

单边谱

这里是傅立叶级数的普通形式
$$\left\{\begin{array}{c}{A}_n(幅度)\sim \omega \\ {\phi }_n(相位)\sim \omega \end{array}\right\}$$
$$A_n=\sqrt[]{a_n^2+b_n^2}n=1,2,\mathrm{3...}$$

双边谱

这里是傅立叶级数的复数形式
$$\left\{\begin{array}{c}\left|F_n(幅度)\right|\sim \omega \\ {\phi }_n(相位)\sim \omega \end{array}\right\}$$
$$\left|F_n\right|=\frac{A_n}{2}n=0,\pm 1,\pm 2,...$$

例子：周期矩形波信号

我拿GeoGebra画了一个很粗略的表示，这个其实是周期性的，就是他其实是无限个矩形波函数，大家应该都懂我意思🤪

$$矩形波信号：幅度为1宽度为\tau 周期为T$$
我们求其频谱也就是求傅立叶级数的系数Fn

求其傅立叶级数的Fn

$$\begin{array}{rl}Fn& =\frac{1}{T}{\int }_{-\frac{\tau }{2}}^{\frac{\tau }{2}}f(t)e^{-jn\Omega t}dt\\ & =\frac{1}{T}{\int }_{-\frac{\tau }{2}}^{\frac{\tau }{2}}{e}^{-jn\Omega t}dt\\ & =\frac{1}{T}\frac{1}{-jn\Omega }{e}^{-jn\Omega t}{|}_{-\frac{\tau }{2}}^{\frac{\tau }{2}}\\ & =\frac{1}{T}\frac{1}{-jn\Omega }[e^{-jn\Omega \frac{\tau }{2}}-e^{-jn\Omega (-\frac{\tau }{2})}]\\ & =\frac{1}{T}\frac{1}{-jn\Omega }[-2jsin(n\Omega \frac{\tau }{2})]\\ & =\frac{2}{T}\frac{sin(\frac{n\Omega \tau }{2})}{\frac{n\Omega \tau }{2}}\cdot \frac{\tau }{2}\\ & =\frac{\tau }{T}Sa(\frac{n\Omega \tau }{2})(n=0,\pm 1,\pm \mathrm{2...})\end{array}$$
$$\begin{gathered} 我们已知抽样函数Sa(x)函数=\frac{sinx}{x} \\ \tau 是信号宽度,T是信号周期 \end{gathered}$$

画出其频谱图

先画出Sa函数，注意坐标轴，我这里为了方便显示，取了几个具体的数值，实际上要根据题中的条件计算。

clear
close all
clc

% 定义时间轴t和信号x
t = -16:0.01:16;
x = (0.25)*sinc(t / pi);

% 绘制原始信号
plot(t, x, '--','LineWidth', 3);
xlabel('时间');
ylabel('幅度');
title('Sa(t)');
grid on;
hold on;

% 进行1/4倍采样
x_downsampled = downsample(x, 80);

% 计算新的时间轴
t_downsampled = t(1:80:end);

% 绘制降采样后的信号
stem(t_downsampled, x_downsampled, 'LineWidth', 3);
xlabel('w');
ylabel('Fn');
title('频谱图');
legend('频谱信号', '谱线');
grid on;

$$\begin{gathered} 我们设T=4\tau Fn=\frac{1}{4}Sa(\frac{n\Omega \tau }{2}) \\ 则零点\frac{n\Omega \tau }{2}=\pi m\Rightarrow n\Omega =\frac{2m\pi }{\tau } \end{gathered}$$

两个零点之间有4条谱线，这些谱线的位置和数量取决于信号的采样率和矩形波函数的宽度。
$$\begin{gathered} 两个零点之间有4条谱线,谱线间隔为\Omega \\ \frac{\omega }{\Omega }=\frac{\frac{2\pi }{\tau }}{\frac{2\pi }{T}}=4 \\ 最高点是0.25 \end{gathered}$$

$$\Omega =\frac{2\pi }{T}=2\pi f$$
因为周期门函数在时域是周期连续的，所以他在频谱上就是非周期离散的。

对应关系

时域/频域	时域/频域
周期	离散
非周期	连续

举个例子：

• 矩形波函数在时域是连续周期的，那么他在频谱上就是非周期离散的。
• 门函数做傅立叶变换后就是Sa函数，如果把它在时域上周期化，那他的频谱就被离散化了，也就是变成了上图的样子，包络是一个Sa函数，但是谱线是离散的。

特点

1. 周期信号频谱是离散谱（谐波性）。
2. 谱线所处的位置是基频Ω的整数倍。
3. 一般具有收敛性，总趋势减小。

T不变，改变τ，观察三个脉冲时间不同的矩形波信号

$$函数g_{\tau }(t)=\frac{\tau }{T}Sa(\frac{n\pi \tau }{T})$$

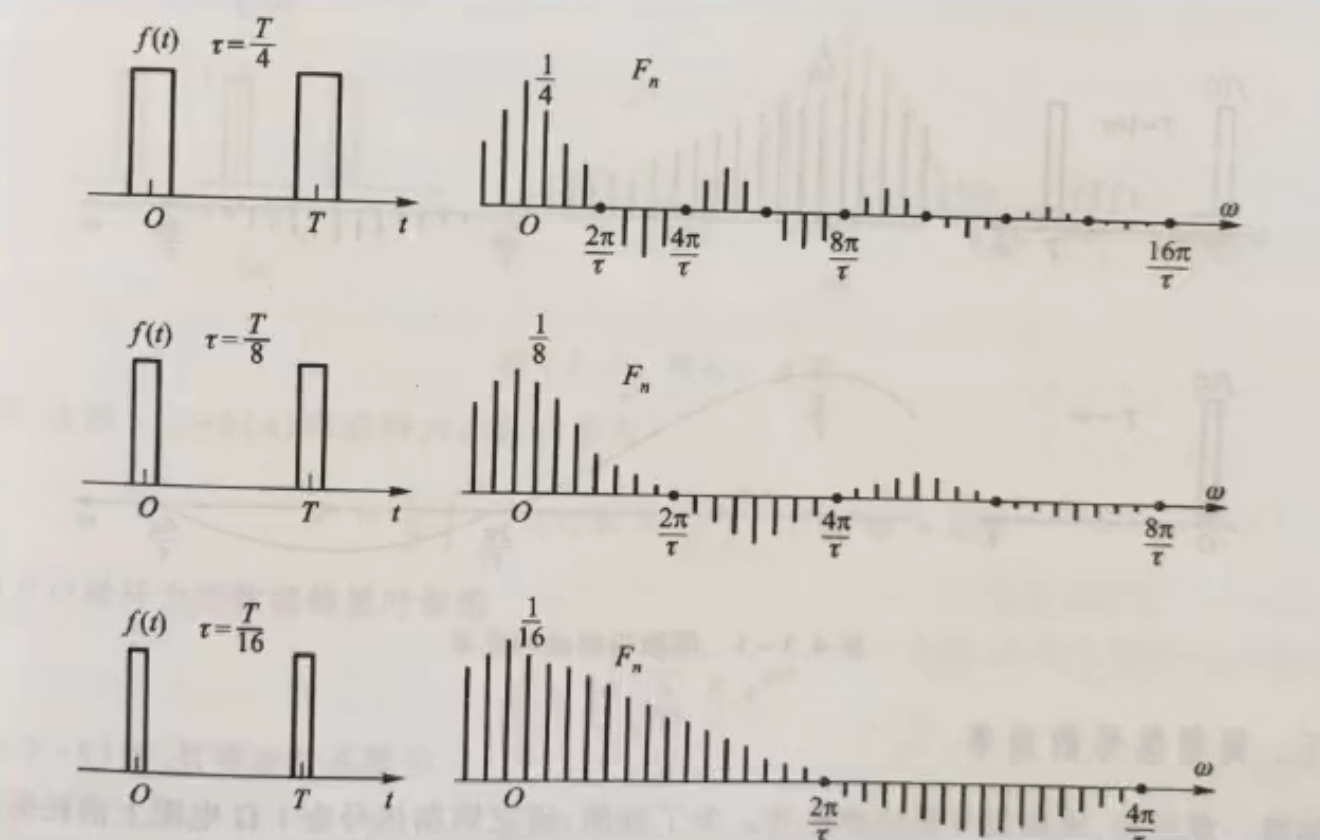
结论

观察这些图，我们可以得到结论：
$$若T不变\tau 减小\{\begin{array}{c}1.最大点\frac{\tau }{T}\downarrow \\ 2.谱线间隔不变\\ 2.零点向右移动，零点横坐标变大了\\ 4.谱线数目\frac{T}{\tau }\end{array}$$

$$当\tau ⟶0,图像会变成一条直线，也就是我们说的冲激函数\delta (t)$$

τ不变，改变T，观察四个周期不同的矩形波信号

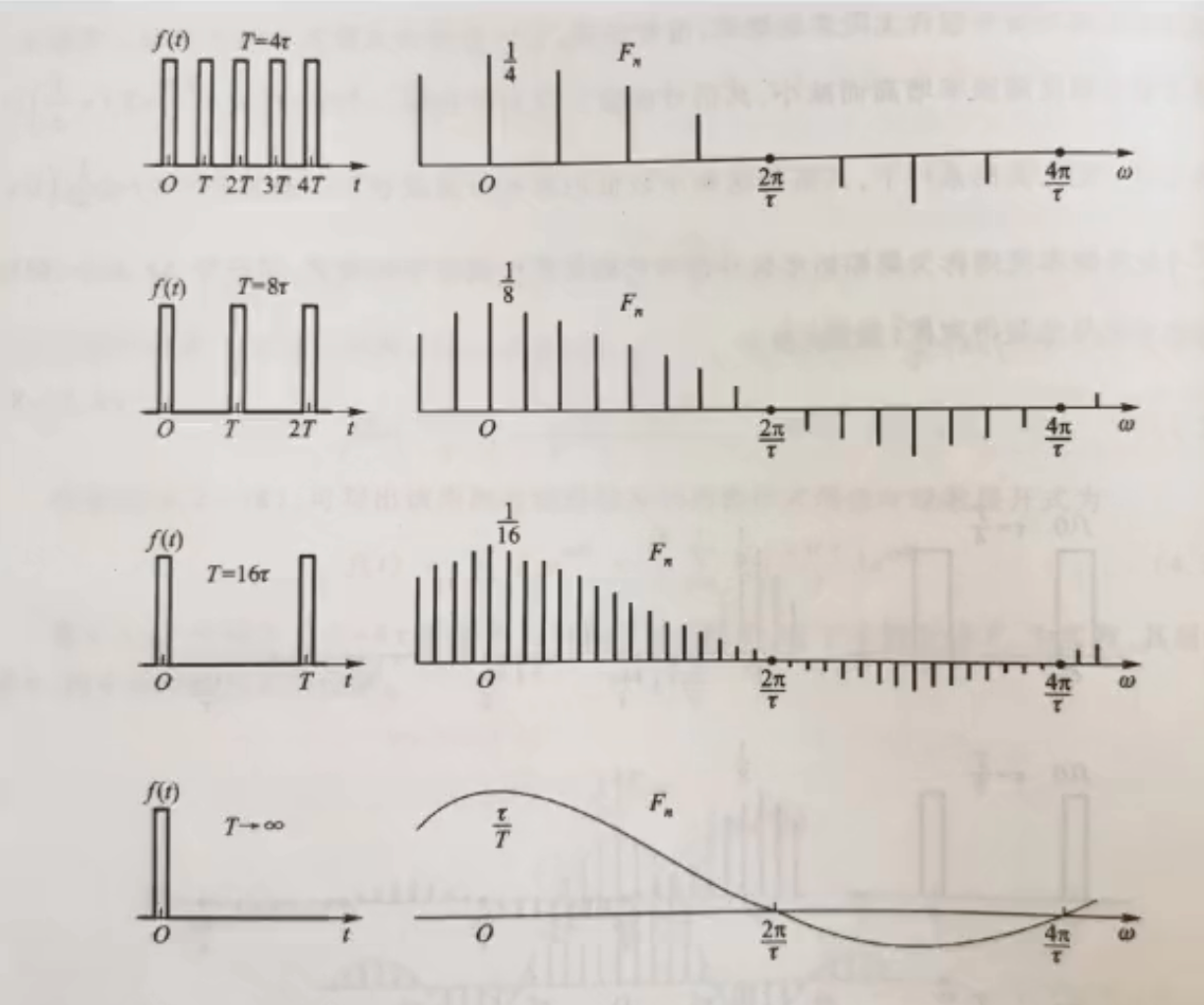
$$若\tau 不变，T增加\{\begin{array}{c}最大值\frac{\tau }{T}\downarrow \\ 右图谱线间隔\Omega =\frac{2\pi }{T}\downarrow ,当T\to \infty ，\Omega \to 0\\ 零点\frac{2m\pi }{\tau },\tau 不变,0点不变\\ 谱线数\frac{T}{\tau }\uparrow ,谱线数\to \infty \end{array}$$

结论

我们重点看一下最后一个图，当T趋于∞，周期信号的周期无穷大，那么他就变成了非周期信号，上图只留下了一个矩形，是能量信号，频域变成了连续函数。

可以说是由傅里叶级数，因为其周期无穷大，所以变成了傅里叶变换，信号的频谱由离散谱变成了连续谱，同时各频率分量趋于无穷小。

我们知道：
$$n\Omega =\frac{2\pi }{T}n,T\to \infty ,n\Omega \to 0$$
上面的公式是什么意思呢，就是频域的离散函数变成了连续函数，因为每一个谱线的间隔的无限小。
$$在数学上，当\Omega \to 0时,我们称其为\omega$$

其实最后一个图像我们就从傅立叶级数得到了傅立叶变换——计算非周期信号的频谱。关于其数学公式的推导，我也写了一篇博客但是因为公式实在太多，只推导了一部分，后期我会把坑填上的。

频谱密度

定义

定义：为了描述非周期信号的频谱特性，引入的概念称为频谱密度。

我们常说的密度是连续的，所以那频谱密度也是连续的，这里我给个频谱密度一个定义，是指信号单位频率下的能量。

频谱密度函数$F\left(\omega \right)$公式

$$F\left(\omega \right)=\underset{T\to \infty }{\lim }\frac{F_n}{1/T}=\underset{T\to \infty }{\lim }{F}_n\cdot T=\underset{w\to 0}{\lim }\frac{F_n\cdot 2\pi }{w}$$
在这里$F_n$(指数型傅里叶级数的系数)是趋于无穷小的，$T$是趋于无穷大的，所以这两者相乘是一个常数。

---

但是话又说回来，为什么频谱密度要叫频谱密度呢，他和普通的频谱到底有什么区别？

想象有一块石头，他的质量是m，他的体积是v，根据密度公式，我们很容易算出他的密度是多少，那加入我们取石头上非常非常小的一块，它的质量趋于0，它的体积也趋于0，那么怎么用物理量来表示呢，这时就要引出密度的概念了，无穷小的质量/无穷小的体积得到的常数，就是这一小块的密度了。

所以频谱密度也是一样的道理，$F\left(j\omega \right)={\lim }_{w\to 0}\frac{F_n\cdot 2\pi }{\omega }$。因为各个频率分量的幅度是无穷小的，给他除一个很小的频带宽度$\omega$就能得到一个常数。

我们在上面已经说了，连续的频谱基频Ω趋于0，对照着下面这图像

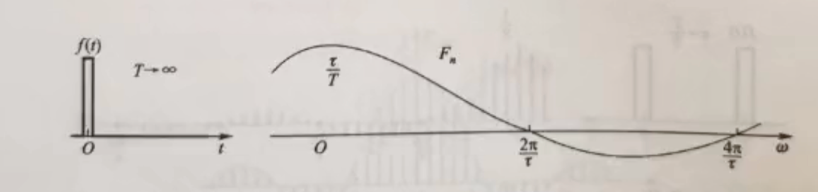
我们可以知道，连续频谱在时域上是非周期的。所以，当我们谈论谱密度时，就已经是默认这个信号在时域上是非周期的，频谱是连续的了。

这里我们需要引入能量信号，他的能量是有限的，所以他一定是一个非周期函数，所以严格地说，他不能用傅立叶级数去计算他的频谱，他只能用傅立叶变换去计算他的频谱密度。

关于周期信号的频谱密度，我参考了这一篇文章：频谱和频谱密度在概念和适用方向上有哪些区分？ - 張無忌的回答 - 知乎

周期功率信号 的功率只集中分布在基频的倍频上，因而，功率在频域是离散分布的，如果严格地套用谱密度的意义，其谱密度应该是一连串冲击函数，这类包含无穷的特殊函数对应用而言是没有意义的。有时为了与非周期信号统一表示，会将集中分布的功率近似平均到相邻倍频的区间内，形式上也就变成频谱密度，但应当了解，这是近似的，并不是周期信号原始的属性。

举个例子，在这幅图中，我们可以将集中分布的功率近似分布到相邻的倍频区间内，他也就变成连续的了。

非周期功率信号 对应的直接就是频谱密度。

还有需要了解的是，对能量信号和功率信号的分析中，虽然有时两者的分析中都称谱密度，但能量信号的谱密度是 能量的谱密度 ，而功率信号的谱密度指的是 功率的谱密度 ，二者在计算上有区别的，相差了一个时间平均，不应混淆。

傅里叶正变换公式

由上文的公式
$$F\left(\omega \right)=\underset{T\to \infty }{\lim }\frac{F_n}{1/T}=\underset{T\to \infty }{\lim }{F}_n\cdot T=\underset{w\to 0}{\lim }\frac{F_n\cdot 2\pi }{w}$$
以及
$$F_n=\frac{1}{T}{\int }_{-\frac{T}{2}}^{\frac{T}{2}}f\left(t\right)e^{-jn\omega t}dt$$
将$F_n$代入$F\left(j\omega \right)={\lim }_{T\to \infty }{F}_n\cdot T$得

$$F\left(\omega \right)={\int }_{-\frac{T}{2}}^{\frac{T}{2}}f\left(t\right)e^{-jn\omega t}dt$$
因为傅里叶变换的情况是$T$趋于无穷，$\omega$趋于0，$n\omega$变成连续的了，所以傅里叶正变换公式就是

$$F\left(\omega \right)={\int }_{-\infty }^{\infty }f\left(t\right)e^{-j\omega t}dt$$

傅里叶逆变换公式

先看傅里叶级数的指数形式
$$f\left(t\right)=\sum _{n=-\infty }^{\infty }{F}_n{e}^{jn\omega t}$$
为了凑出$F(\omega )$，我们要这样处理
$$f\left(t\right)=\sum _{n=-\infty }^{\infty }{F}_{n}T{e}^{jn\omega t}\cdot \frac{1}{T}$$
我们令$T\to \infty$，则$\omega \to 0$，取其为$d\omega$，我们就可以将上式的$\frac{1}{T}$改为$\frac{2\pi }{T}\cdot \frac{1}{2\pi }$，$\omega$趋于0，$n\omega$变成连续的了，求和符号应变为积分符号，所以$f(t)$最后为

$$f\left(t\right)=\frac{1}{2\pi }{\int }_{-\infty }^{\infty }F(\omega )e^{j\omega t}d\omega$$
这就是傅里叶逆变换。

总结

我们一般在分析信号的时候，要先确定其信号类型，如果是非功率非能量信号，则要用广义函数和分布对其进行分析，但是话说回来，我看了这么多还真没遇到过这样的，如果我以后遇到了再来填坑。确定其信号类型之后，我们要根据其类型再去分析：如果是能量信号，看看是周期信号还是非周期信号(通常是非周期信号)，再对其进行傅立叶变换，假如是功率信号，判断其是周期信号还是非周期信号，要注意只有周期功率信号才有频谱(因为可以做傅立叶级数)，非周期功率信号和能量信号是没有频谱的，只有频谱密度(只能做傅立叶变换)。或者说周期性的功率信号频域是离散的，其他信号频域是连续的。

最新的想法

后来我又从书上了解到，周期性的功率信号展开成傅里叶级数的系数是频谱。

非周期性的能量信号的傅里叶变化是频谱密度

频谱是离散谱，频谱密度是连续谱

频谱的单位是伏（V），频谱密度的单位是伏/赫兹（V/Hz）。

由于非周期信号，我们将其视作周期无限的信号，所以他在一点频率的幅度为0，我问老师，老师说，非周期信号的频谱密度，在某一小区间面积才能计算。