👨‍🏫🥰🥳需要机械臂相关资源的同学可以在我的CSDN主页中寻找哦🤖😽🦄

指南目录📖：

🎉🎉机械臂速成小指南（零点五）：机械臂相关资源🎉🎉

机械臂速成小指南（零）：指南主要内容及分析方法

机械臂速成小指南（一）：机械臂发展概况

机械臂速成小指南（二）：机械臂的应用

机械臂速成小指南（三）：机械臂的机械结构

机械臂速成小指南（四）：机械臂关键部件之减速机

机械臂速成小指南（五）：末端执行器

机械臂速成小指南（六）：步进电机驱动器

机械臂速成小指南（七）：机械臂位姿的描述方法

机械臂速成小指南（八）：运动学建模（标准DH法）

机械臂速成小指南（九）：正运动学分析

机械臂速成小指南（十）：可达工作空间

机械臂速成小指南（十一）：坐标系的标准命名

机械臂速成小指南（十二）：逆运动学分析

机械臂速成小指南（十三）：轨迹规划概述

机械臂速成小指南（十四）：多项式插值轨迹规划

机械臂速成小指南（十五）：线性规划

机械臂速成小指南（十六）：带抛物线过渡的线性规划

机械臂速成小指南（十七）：直线规划 

机械臂速成小指南（十八）：圆弧规划

机械臂速成小指南（十九）：机械臂的电路板抓取实验

机械臂速成小指南（二十）：机械臂的位姿重复性实验

机械臂速成小指南（二十一）：几何雅可比矩阵

机械臂速成小指南（二十二）：机械臂逆运动学的数值解方法

机械臂速成小指南（二十三）：Paul方法求解机械臂运动学逆解（含matlab代码） 

🦾🌏🪐以下为正文🦾🌏🪐

六自由度机械臂上位机python代码（带详细注释，含正逆运动学及轨迹规划等）https://download.csdn.net/download/m0_53966219/87521956?spm=1001.2014.3001.5503六自由度机械臂下位机代码及pcb设计https://download.csdn.net/download/m0_53966219/88480657?spm=1001.2014.3001.5503

        我认为，机械臂的运动学分析就是为了解决两个问题：

1. 如何通过各关节的旋转角度（关节变量）得到机械臂末端执行器的位姿
2. 如何通过机械臂末端执行器的位姿得到各关节的旋转角度（关节变量）

        在运动学分析的过程中，我们仅研究机械臂的运动特性，而不考虑使机械臂产生运动时力的大小以及机械臂本身的物理性质。因此，我们将机械臂的各个部分视为刚体，并分析机械臂的位姿、转动过程、角速度、角加速度等较复杂的运动特征。

        刚体（Rigid body）是指在运动中和受力作用后，形状和大小不变，而且内部各点的相对位置不变的物体。位姿即位置与姿态，而准确、简洁地描述机械臂的位姿是对机械臂展开运动学分析的重要前提，下面，我们将分析描述机械臂（下称刚体）的位姿描述方法。

注：本章中所使用的画图软件为geogebra。

一、刚体的位姿

        为了描述机器人的位置和姿态,需要建立坐标系。在机器人学中,通常采用笛卡尔坐标
系(Cartesian Frame)，就是常用的三轴正交坐标系。

        笛卡尔（Rene Descartes,1596-1650）是法国著名的哲学家、数学家、物理学家，他创立了著名的平面直角坐标系，使得几何形状可以用代数公式明确表达出来，因将笛卡儿坐标体系公式化而被称为解析几何之父，常用的直角坐标系也被称为笛卡儿坐标系在笛卡儿所处的时代，拉丁文是通用的学术语言，笛卡儿通常会在他的著作上签上他的拉丁名字 Renatus Cartesius，而 Cartesian 是 Cartesius 的形容词形式，所以他创立的直角坐标系被称为 Cartesian Frame。

        笛卡尔的姓 Descartes（法语）是由 des 和 Cartes 组成的复合词对应的英文是“of the Maps”，这说明笛卡尔的祖先可能是从事地图绘制的。

1.1    刚体的位置

        如下图所示，设O-x0y0z0 为一空间笛卡尔直角坐标系，a0 、b0 、c0 是平行于各坐标轴的单位向量，O1 为一刚体质心。

        点O' 相对于参考坐标系O-x0y0z0 的位置可以表示为关系式

        式中o1x 、o1y 、o1z 是向量o1∈R3 在参考坐标轴上的分量。由此，刚体质心O1 相对于参考坐标系的位置可以表示为一个(3×1) 向量，该向量称为刚体的位置向量

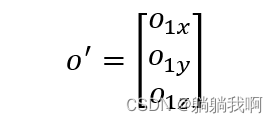
1.2    刚体的姿态

        为描述刚体在空间中的姿态，设O1-x1y1z1 为一空间笛卡尔直角坐标系且与刚体固连，如下图所示。

        其中，a1 、b1 、c1 是刚体坐标系的单位向量，每一单位向量的分量都是刚体坐标系O1-x1y1z1 的坐标轴相对参考坐标系O-x0y0z0 的方向余弦。a1 、b1 、c1 在参考坐标系O-x0y0z0 可表示为：

        综上，刚体在空间中的位置可通过刚体上一点（本文选择刚体的质心）相对于参考坐标系的位置来表示，而刚体在空间中的姿态可通过与刚体相固连的坐标系（刚体坐标系原点同样选择刚体的质心）相对于参考坐标系的单位向量的三个分量来表示。

        机械臂作为一开运动链，其姿态为构成机械臂的所有连杆的姿态。

二、旋转矩阵（Rotation matrix）

        上文中我们引出位置向量来描述刚体的位置，那么，我们选用什么来描述刚体的姿态呢？

2.1    基本旋转

        上述的刚体坐标系显然可由参考坐标系通过一系列的平移与旋转得到，其中，旋转过程可由1到3次的基本旋转组合而成。

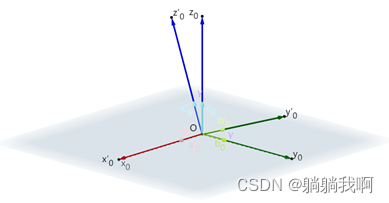
      不妨令参考坐标系O-x0y0z0 绕z0 轴旋转角度α(α>0) ，得到坐标系O-x0'y0'z0' ，如下图所示

        新坐标系O-x0'y0'z0' 的各单位向量可通过其相对于参考坐标系O-x0y0z0 的分量来描述，即 

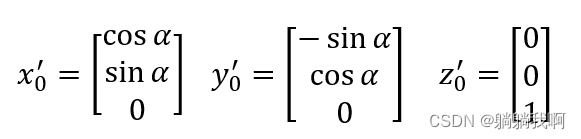
        从而我们可以得出新坐标系O-x0'y0'z0' 关于参考坐标系O-x0y0z0 的旋转矩阵为

        旋转矩阵Rz 描述了参考坐标系绕z0轴的旋转。

        同理，将参考坐标系O-x0y0z0 绕y0 轴旋转角度β(β>0) 以及将其绕x0 轴旋转角度γ(γ>0) 的基本旋转可分别表示为

 所得到的新坐标系分别如图a以及图b所示

a.参考坐标系绕坐标轴y0 的基本旋转	b.参考坐标系绕坐标轴x0 的基本旋转

 2.2   空间中向量的旋转

        旋转矩阵也可视为使某一向量绕空间中任一轴旋转给定角度的矩阵算子。设参考坐标系O-x0y0z0 与另一坐标系O-x1y1z1 原点重合，则此时有

        Q 为空间中一点，在不同坐标系下的表示如下图所示

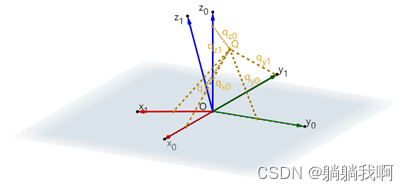
        点Q 相对于参考坐标系O-x0y0z0与O-x1y1z1可分别表示为

点Q 相对于参考坐标系O-x0y0z0	点Q 相对于参考坐标系O-x1y1z1

        q 与q' 均表示的是点Q ，则有

        同时，由于旋转矩阵具有正交性，则上的逆变换为

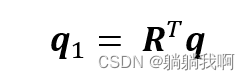
        现将q 与q1 视为参考坐标系O-x0y0z0 中向量，二者模值相等，且可将q 看作在参考坐标系中，q1 按照旋转矩阵R 旋转后得到的。

        因此，旋转矩阵是将向量在同一坐标下进行旋转的算子,且可用于表示两坐标系之间的相对指向，这两个性质相互等价。

        综上，一个旋转矩阵具有三个等价的几何学意义：

• 描述两个坐标系之间的相对指向。其列向量为旋转后坐标系中的轴关于原坐标系中的轴的方向余弦；
• 表示同一点在两个不同坐标系（原点重合）下坐标直接的变换关系；
• 将向量在同一坐标系中进行旋转的算子。

2.3    旋转矩阵的合成

        设O-x0y0z0 、O-x1y1z1 及O-x2y2z2 为三个共原点的坐标系，而Rij 表示坐标系i 关于坐标系j 的旋转矩阵。设q 为描述空间中某点Q 位置的向量，q 、q1 及q2 分别为向量q 在三个坐标系中的表示。则

        将上面三个等式联立可得

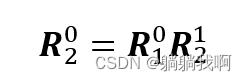
        由上式可知，一次旋转可以由一系列的部分旋转组合而成，当旋转矩阵以右乘的方式组合时，表示每一个部分旋转是根据上一个旋转定义的。这个式子可看作两次部分旋转的合成，即按照给定的顺序右乘旋转矩阵，且第二个部分旋转相对于第一个旋转定义。

        同时，连续旋转中的部分旋转也可以一直相对于一个固定的坐标系进行定义，但是此时旋转矩阵的合成方式变为左乘，即

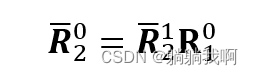
 显然，此处的 与 并不相等。

         在旋转合成中需要注意，矩阵乘法不满足交换律，由此我们可以推断：通常情况下，两个旋转不可交换顺序，且其合成关系依赖于单个旋转的顺序。这个性质我们可以用下面两幅图来判断：

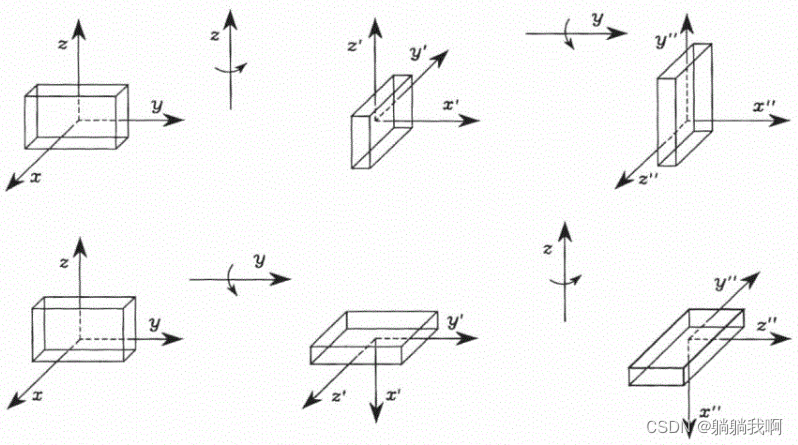三、欧拉角（Euler angles）

        上一章中我们讨论了使用旋转矩阵来描述刚体的姿态，但是，这种方法存在两个问题：

• 旋转矩阵对于坐标系姿态的描述是冗余的
• 无法直观地描述姿态，抽象且不易于理解

        出现这种状况是因为旋转矩阵是正交矩阵，它的9个元素之间并不是相互独立的，因此，我们使用旋转矩阵描述某坐标系的朝向是冗余的。

        特殊正交群(special orthogonal group)一类元素行列式为1的重要的典型群。正交群On(K，Q)的元素的行列式都是1或-1，其中行列式为1的全体正交变换组成一个子群，称为特殊正交群，记为SOn(K，Q)，刚体的旋转矩阵为特殊正交群。

        特殊正交群SO(m)的最简表示需要m(m-1)/2 个参数。（这个定义来自Siciliano B, Sciavicco L, Villani L, etal. Robotics Modelling, Planning and Control[M]. 978-1-84628-641-4. London:Springer , 2009 :4-4.）因此，我们选用欧拉角中的RPY角作为描述机械臂的姿态的第二种方法。

        将参考坐标系绕x 轴、y 轴、z 轴所旋转的角度分别定义为φ 、θ 、ψ ，对应的基本旋转矩阵Rz (φ) 、Ry (ϑ) 、Rx(ψ) 可由上一章节中的公式得出。坐标系的最终指向通过左乘基本旋转矩阵得出，可表示为

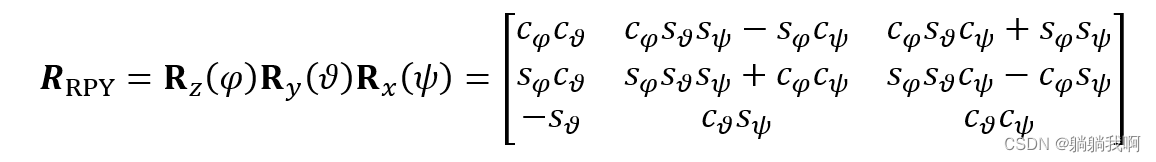        进而可得到φ 、θ 、ψ 的角度值为

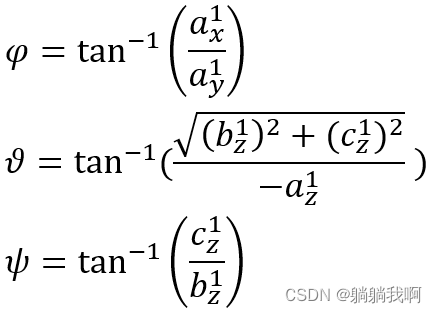
四、齐次变换矩阵（Homogeneous transformation matrix）

        如下图所示，空间中有坐标系O-x0y0z0 与O1-x1y1z1 ，Q 为空间中任一点。

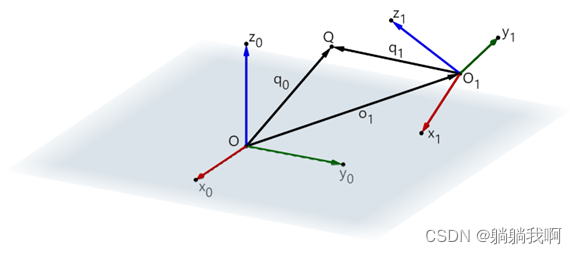
        其中，q0 为点Q 相对坐标系O-x0y0z0 （下称坐标系0）的坐标向量；o1 为坐标系O1-x1y1z1 （下称坐标系1）原点在坐标系0中的位置表示；q1 为点Q 相对与坐标系1的坐标向量；R10 为坐标系1相对于坐标系0的旋转矩阵。有如下关系

        上式可看作有界向量q 在坐标系0与坐标系1之间由于平移与旋转所带来的坐标变换。为得到对一点在不同坐标系下的齐次表示，本文首先在一般向量q 上添加一单位元素构成 ，即

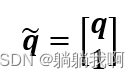
        进而引入一(4×4)矩阵

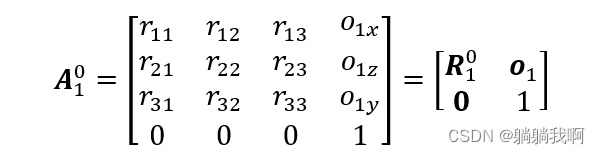
        该矩阵即为齐次变换矩阵，是位移与旋转的复合表示，该矩阵属于特殊欧几里得群（special Euclidean group）。显然齐次变换矩阵不具有正交性。

        由此，对于任一向量的一系列坐标变换可以表示为

        齐次变换矩阵是两坐标系之间的坐标变换的简洁表示。若两个坐标系的坐标原点相同，则其次变换矩阵将退化为旋转矩阵。

六自由度机械臂上位机python代码（带详细注释，含正逆运动学及轨迹规划等）https://download.csdn.net/download/m0_53966219/87521956?spm=1001.2014.3001.5503