一、背景介绍

1.题目

给定n个矩阵{A₁,A₂,…,A_n} ， 其中A_i与A_i+1 是可乘的i=1,2,…n-1, 考察这n个矩阵的连乘积 ： A₁A₂…A_n

矩阵连乘具有许多计算顺序
原因：矩阵乘法满足结合律；
这种计算次序可以用加括号的方式来确定。

完全加括号
若一个矩阵连乘积的计算次序完全确定，也就是说该连乘积已完全加括号；
则可以依此次序反复调用2个矩阵相乘的标准算法计算出矩阵连乘积。

2.示例

因为矩阵乘法符合结合律，所以在计算ABC时，有两种方案，即**(AB)C和A(BC)**。
①对于第一方案(AB)C，计算：

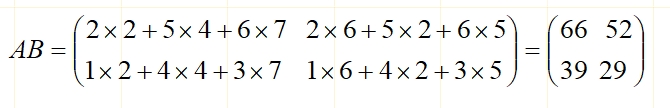
其乘法运算次数为：2×3 ×2=12

其乘法运算次数为：2×2×4=16。
总计算量为：12+16=28

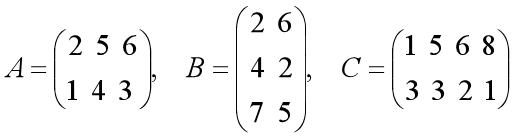
②对第二方案 A(BC)，计算：

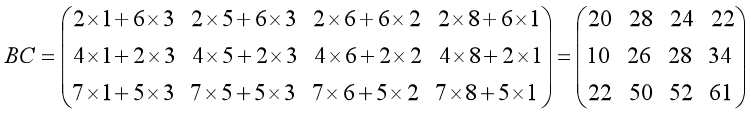
其乘法运算次数为：3×2×4=24

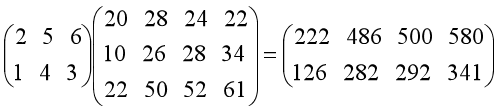
其乘法运算次数为：2×3×4=24。
总计算量为：24+24=48
可见，不同方案的乘法运算量可能相差很悬殊。

3.矩阵乘积的标准算法(第五版P47)

附加示例：不同的计算顺序——不同的时间复杂度

设有四个矩阵A,B,C,D，它们的维数分别是：A=50×10，B=10×40，C=40×30，D=30×5。
总共有五种完全加括号的方式：(A((BC)D)) (A(B(CD))) ((AB)(CD)) (((AB)C)D) ((A(BC))D)。
其数乘次数分别为：
(A((BC)D)):(BC) 10×40×30=12000 (定义为：F:10×30)
(FD) 10×30×5=1500 (定义为：G:10×5)
(AG) 50×10×5=2500
(A((BC)D))的次数=12000+1500+2500=16000
同理可计算其他4种情况：10500, 36000, 87500, 34500。

给定n个矩阵｛A1,A2,…,An｝，其中Ai与Ai+1是可乘的，i=1，2…，n-1。如何确定计算矩阵连乘积的计算次序，使得依此次序计算矩阵连乘积需要的数乘次数最少？

---

二、动态规划解题思路

1.分析最优解的结构

特征：计算A[i:j]的最优次序所包含的计算矩阵子链 A[i:k]和A[k+1:j]的次序也是最优的。

最优子结构性质：
矩阵连乘计算次序问题的最优解包含着其子问题的最优解。这种性质称为最优子结构性质。
问题的最优子结构性质是该问题可用动态规划算法求解的显著特征。

2.建立递归关系

设计算A[i:j]，1≤i≤j≤n，为所需要的最少数乘次数m[i, j]，则原问题的最优值为m[1, n]。
当i=j时，A[i:j]=Ai，因此，m[i, i]=0，i=1,2,…,n；
当i<j时，这里 A_i的维数为 p_i-1xp_i

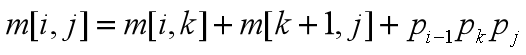
可以递归地定义m[i, j]为：

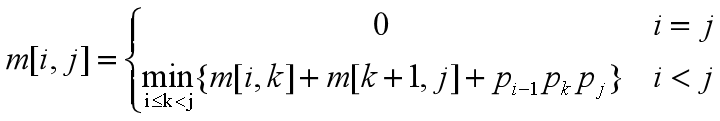
k的位置只有 j-i 种可能。

这个递归公式假设已知k的值，而实际上并不知道。不过k的位置只有j-i种可能。
m[i:j]给出了子问题的最优解，即计算A[i:j]所需要的最少数乘次数。同时还确定了计算A[i:j]的最优次序中的断开位置k，在该处分裂乘积A[i:j]后可得到最优完全加括号方式。
定义数组s[i:j]保存k的值，在计算岀最优值m[i:j]后，可递归地由s[i:j]构造出相应的最优解。

3.计算最优值

对于1≤i≤j≤n不同的有序对(i, j)对应于不同的子问题。因此，不同子问题的个数最多只有:

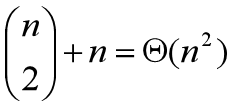
由此可见，在递归计算时，许多子问题被重复计算多次。这也是该问题可用动态规划算法求解的又一显著特征。
用动态规划算法解此问题，可依据其递归式以自底向上的方式进行计算。在计算过程中，保存已解决的子问题答案。每个子问题只计算一次，而在后面需要时只要简单查一下，从而避免大量的重复计算，最终得到多项式时间的算法


…
M[1][6]=m[1][1]+m[2][6]+p[0]p[1]p[6]=0+ 10500 +303525=36750
M[1][6]=m[1][2]+m[3][6]+p[0]p[2]p[6]= 15750+ 5375 +301525=32375
M[1][6]=m[1][3]+m[4][6]+p[0]p[3]p[6]= 7875+ 3500 +30525=15125
M[1][6]=m[1][4]+m[5][6]+p[0]p[4]p[6]= 9375+5000+ 301025=21875
M[1][6]=m[1][5]+m[6][6]+p[0]p[5]p[6]= 11875+0+302025=26875

void MatrixChain(int *p，int n，int **m，int **s) // p矩阵的维数
{
        for (int i = 1; i <= n; i++) m[i][i] = 0;
        for (int r = 2; r <= n; r++)
           for (int i = 1; i <= n - r+1; i++) {
              int j=i+r-1;
              m[i][j] = m[i+1][j]+ p[i-1]*p[i]*p[j];    //m[i][j]初始为Ai(Ai+1Ai+2…Aj)的次数
              s[i][j] = i;
              for (int k = i+1; k < j; k++) {
                 int  t = m[i][k] + m[k+1][j] + p[i-1]*p[k]*p[j];
                 if (t < m[i][j]) { m[i][j] = t; s[i][j] = k;}
              }
          }
}

算法复杂度分析：
算法matrixChain的主要计算量取决于算法中对r，i和k的3重循环。循环体内的计算量为O(1)，而3重循环的总次数为O(n3)。因此算法的计算时间上界为O(n3)。算法所占用的空间显然为O(n2)。

4.构造最优解

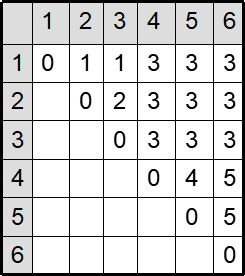
算法 MatrixChain只是计算了最优值，并未给出最优解；
S[i][j]中记录了矩阵链应从哪个位置断开。
例如：
S[1][6]=3,即A[1:6]从3的位置断开
A[1:3]和A[4:6]两段(A1A2A3)(A4A5A6)
S[1][3]=1 (A1(A2A3))
S[4][6]=5 ((A4A5 ) A6)

void Traceback(int i, int j, int **s)
{ 
       if(i==j) return;
       Traceback(i, s[i][j], s);
       Traceback(s[i][j]+1, j, s);
       cout<<“Multyply A ”<<i<<“,”<<s[i][j];
       cout<<“ and A ”<<(s[i][j]+1)<<“,”<<j<<endl;
}

5.测试代码

#include <iostream>

using namespace std;

/* run this program using the console pauser or add your own getch, system("pause") or input loop */

int MatrixChain_GetOptimalValue(const int *p, int n, int *s)
// p: (in) 矩阵的行数和列数
// n: (in) 矩阵数量
// s: (out) 子链最优断开位置 
// 返回值：最优链的计算量 
{
	int *m=new int [(n+1)*(n+1)];
	// 子链最少计算量 

	for (int i=1; i<=n; i++)
		m[i*(n+1)+i]=0;
	for (int r=2; r<=n; r++) // r是子链的长度 
	{
		for (int i=1; i<=n-r+1; i++) // i是子链的起始位置
		{
			int j=i+r-1; // j是子链的终止位置
			m[i*(n+1)+j]=m[(i+1)*(n+1)+j]+p[i-1]*p[i]*p[j];
			s[i*(n+1)+j]=i;
			
			for (int k=i+1; k<j; k++) // k是子链的断开位置 
			{
				int t=m[i*(n+1)+k]+m[(k+1)*(n+1)+j]+p[i-1]*p[k]*p[j];
				if (t<m[i*(n+1)+j])
				{
					m[i*(n+1)+j]=t;
					s[i*(n+1)+j]=k;
				}
			}
		} 
	}
	
	int result=m[1*(n+1)+n];
	delete [] m;
	
	return result;
}

void MatrixChain_Traceback(int i, int j, int n, const int *s, int *t)
// i, j: (in)子链的起始和终止位置
// n: (in) 矩阵数量
// s: (in) 子链最优断开位置 
// t: (out) 每个矩阵左侧'('的数量和右侧')'的数量
{
	if (i==j) return;
	int k=s[i*(n+1)+j];
	MatrixChain_Traceback(i, k, n, s, t);
	MatrixChain_Traceback(k+1, j, n, s, t);
	if (i!=k)
	{
		t[i+i]++;
		t[k+k+1]++;
	}
	if (k+1!=j)
	{
		t[k+k+2]++;
		t[j+j+1]++;
	}
}

void MatrixChain_PrintResult(int n, const int *t)
// n: (in) 矩阵数量
// t: (in) 每个矩阵左侧'('的数量和右侧')'的数量
{
	for (int i=1; i<=n; i++)
	{
		for (int k=0; k<t[i+i]; k++)
			cout<<'(';
		cout<<'A'<<i;
		for (int k=0; k<t[i+i+1]; k++)
			cout<<')';
	}
	cout<<endl;
}

void MatrixChain(const int *p, int n)
// p: (in) 矩阵的行数和列数
// n: (in) 矩阵数量
{
	int *s=new int [(n+1)*(n+1)]; // 子链最优断开位置
	int *t=new int [n+n+2]; // 每个矩阵左侧'('的数量和右侧')'的数量
	for (int i=2; i<=n+n+1; i++) t[i]=0;
	
	int result=MatrixChain_GetOptimalValue(p, n, s);
	MatrixChain_Traceback(1, n, n, s, t);
	cout<<"最少计算量="<<result<<endl;
	cout<<"最优乘法顺序: ";
	MatrixChain_PrintResult(n, t);
	
	delete [] s;
	delete [] t;
}

int main(int argc, char *argv[]) {
	int n=6;
	int p[]={30,35,15,5,10,20,25};
	MatrixChain(p, n);
	
	cin.get();
	return 0;
}