可靠性特征的数学表达式及其关系
下面对于各个特征做逐个的分析
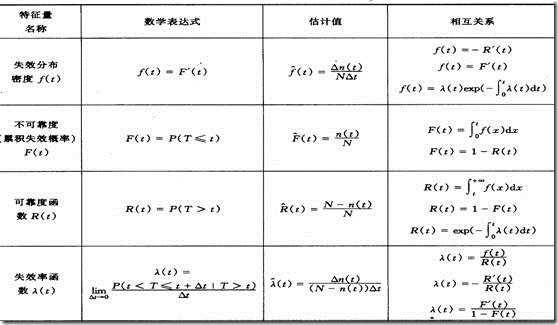
(1)可靠度R(t)
定义:产品在规定条件下和规定时间内完成规定功能的概率(通俗来说,过了规定的时间,产品依然能够正常工作的概率)
数学表达式:R(t)=P(T>t), t为规定时间,T为产品寿命。
估计值:
(2)不可靠度F(t)(累计失效概率)
定义:它是产品在规定的条件下和规定的时间内失效的概率(通俗来说,还没到规定的时间,产品已经不能够使用的概率)
注意:累积失效概率F(t)与可靠度R(t)是相反关系:R(t)+F(t)=1
估计值:
(3)失效概率密度f(t)
定义:是产品在包含t的单位时间内发生失效的概率(通俗来说,在很小的一个时间段内,产品失效的概率)
数学表达式: (F(t)是整个时间段内失效的概率,而f(t)是t内的很小的一段时间失效的概率,正好是F(t)的导数。
估计值:
(4)失效率λ(t)
定义:失效率(瞬时失效率)是:“工作到t时刻尚未失效的产品,在该时刻t后的单位时间内发生失效的概率”(通俗来说,产品在规定的时间内正常的工作,在过了规定时间之后,单位时间内失效的概率)。
估计值:
注意:失效率λ(t)与失效概率密度f(t)的区别
区别主要在:λ(t)考虑的是过了规定时间后单位时间内失效的概率,而f(t)考虑的是没有过规定时间单位时间内失效的概率。过了规定时间的是用没有失效的产品总数求概率。而没有过规定时间是用产品的总数求概率。
(5)R(t)、F(t)、f(t)和λ(t)的相互关系
(5.1)F(t)
F(t)=1-R(t)
(5.2 )λ(t)
公式1
公式推导:
推导过程中:P(A|B)=P(AB)/P(B)
公式推导:
-R’(t)=f(t)
(5.3)R(t)
公式1:R(t)=1-F(t)
公式2:
(5.4)f(t)
f(t)=-R’(t)
f(t)=F’(t)
(6)平均寿命
定义:
不可修产品的平均寿命是指产品失效前的平均工作时间,记为MTTF(Mean Time To Failure);
可修产品的平均寿命是指相邻两次故障间的平均工作时间,称为平均无故障工作时间或平均故障间隔时间,记作MTBF(Mean Time Between Failures)。
公式:
估计值:
(如果仅考虑首次失效前的一段工作时间,两者平均寿命θ估计值)
(7) 可靠寿命、中位寿命和特征寿命

AtomGit 是由开放原子开源基金会联合 CSDN 等生态伙伴共同推出的新一代开源与人工智能协作平台。平台坚持“开放、中立、公益”的理念,把代码托管、模型共享、数据集托管、智能体开发体验和算力服务整合在一起,为开发者提供从开发、训练到部署的一站式体验。
更多推荐
 已为社区贡献2条内容
已为社区贡献2条内容







![clip_image016[1] clip_image016[1]](https://img-blog.csdn.net/20171002214015859)
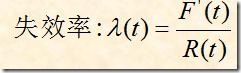
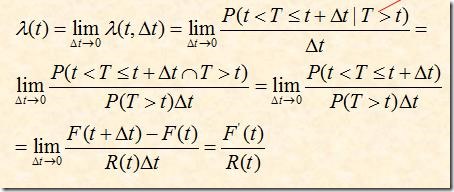
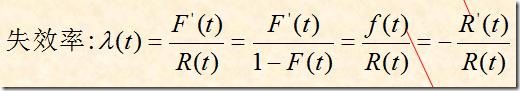
![clip_image016[2] clip_image016[2]](https://img-blog.csdn.net/20171002214021223)

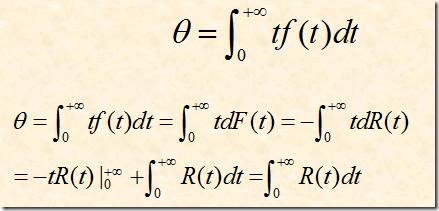









所有评论(0)