傅里叶变化互易对称性

世幻水

28749人浏览 · 2021-01-03 01:13:04

世幻水 · 2021-01-03 01:13:04 发布

互易对称性

若有 $f (t) \leftrightarrow F (j w)$ , 则有 $F (t) \leftrightarrow 2 π f (- w)$

若有 $f (t)$ 是偶函数 , 则有 $F (t) \leftrightarrow 2 π f (w)$

例子1: 求出H(w)=δ(w) 的傅里叶逆变化

解: 已知 $δ (t) \leftrightarrow 1$
则有： $1 \leftrightarrow 2 π δ (w)$
$12π↔δ(w)\frac{1}{2π} ↔ δ(w)$

例子2: 求出H(w)为门函数的傅里叶逆变化

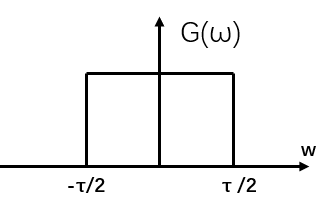
在这里插入图片描述

解：已知门函数的傅里叶变化为Sa(w)函数：
在这里插入图片描述
因为： $τSa(w\frac{τ}{2})$

所以： $τSa(tτ2)↔2πG(w)τSa(t\frac{τ}{2})↔2πG(w)$

$τ2πSa(tτ2)↔G(w)\frac{τ}{2π}Sa(t\frac{τ}{2})↔G(w)$

AtomGit开源社区

AtomGit 是由开放原子开源基金会联合 CSDN 等生态伙伴共同推出的新一代开源与人工智能协作平台。平台坚持“开放、中立、公益”的理念，把代码托管、模型共享、数据集托管、智能体开发体验和算力服务整合在一起，为开发者提供从开发、训练到部署的一站式体验。

更多推荐

1.8B 体积、33 种语言互译｜腾讯混元 HY-MT1.5-1.8B 多语言机器翻译模型上线

在跨语言交流日益频繁的今天，阅读外语菜单、处理多语言邮件、与不同语言背景的人沟通，已经成为很多人日常工作与生活的一部分。过去，这类需求往往依赖联网翻译工具，而如今，—— 一部设备即可支持的相互翻译。当 AI 不再只是“逐字直译”，而是开始理解语境、风格与语言之间的细微差异，机器翻译就真正具备了今天为大家介绍一款高质量、多语言、支持端侧部署的机器翻译模型 ——，现已上线 AtomGit AI 社区，