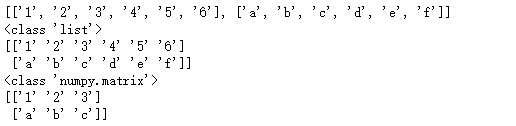
python 数组操作中的 “:” “:: ” “,” “...” python 中的 [:-1] 和 [::-1] [-1:-2:-1] [1:...:1]
使用python版本3.7
首先先了解下python3.7中的下标,python下标有两套,一套是正的,一套是负的
引入负坐标的意义应该是方便将数组中的数据从右往左访问。
a='python'中的python 的下标描述如下
组 p y t h o n
正下标 0 1 2 3 4 5
负下标 -6 -5 -4 -3 -2 -1
对应位置的正下标减去负下标等于len(a) :正下标-负下标=len(a)
使用正下标时,下标i取值范围为0 <= i < len(a) 超出范围为越界,i大于len(a)表示越(数轴)右界
使用负下标时,下标i取值范围为-len(a)-1 < i <=-1 超出范围为越界,i小于len(a)表示越(数轴)左界
数组操作中一般通过 “:” 和数字或变量的组合来灵活使用里面的元素
第一个“:” 表示循环,第二个“:” 表示设定后面数字为步长。比如i:j:k,表示从i到j步长为k,逐个顺次获取。i到j满足左闭右开原则 。
没有冒号表示正常的数组单个元素访问;没有第二个冒号就表示默认的步长为1,从i到j左开右闭步长为1逐个访问。
1、k缺省(忽略未写出的默认值)为1;当k>0时,i缺省为0,j缺省为len(a) ; 当k<0时,i缺省为-1,j缺省为-len(a)-1。
2、当k>0时,可以将i,j全转换成正下标去理解。
当i或j为正且越正数下标右界时,越界的数全部取正下标右界len(a)。
当i或j为负且越负数下标的左界时,越界的数全部取左界前的有效值-len(a),然后再转换成正下标,转换规则为:正下标=len(a)+负下标。
3、当k<0是,可以将i,j全部转换成负下标去理解。
当i或j为负且越负数下标左界时,越界的数全部取负下标左界-len(a)-1。
当i或j为正且越正数下标右界时,越界的数全部取右界前的有效值len(a)-1,然后再转换为负下标,转换规则为:负下标=正下标-len(a)。
4、k不能等于0。
对于循环操作中下标的操作应该先处理越界,然后再根据的正负转换成对应的正负坐标。
a='python' #len(a)=6
i=1
j=4
k=1
b=a[i:j:k] #结果为yth 。意思为从下标i开始到下标j-1结束,步长为k,(k为整数且不能等于0,缺省为1),第一个冒号满足左闭右开原则 。
b=a[i] #结果为y ,无冒号,表示普通的数组单个元素访问,根据下标获取值。
b=a[-1] #结果为n。
b=a[-6] #结果为p。
b=a[i:j] #结果为yth,从i到j,步长为缺省(默认)1
b=a[0:6:1] #结果为python,第一个冒号满足左闭右开原则,等价于a[::]
b=a[0:6:2] #结果为pto,意思为从下标0开始到下标5(6-1)结束,步长为2,等价于a[::2]
b=a[0:6:3] #结果为yo,步长为3,等价于a[::3]
b=a[0:3:1] #结果为pyt,第一个冒号满足左闭右开原则,下标为3的值是取不到的
b=a[0:5:1] #结果为pytho,第一个冒号满足左闭右开原则
b=a[0:7:1] #结果为python,等价于a[0:6:1],当第一个冒号右边的值大于len(a)时,
b=a[0:100:1]#结果为python,此处正下标越界,等价于a[0:6:1],注意第一个冒号右边的100已经超越了正下标的右限。
b=a[6:100:1]#结果为空,等价于a[6:6:1],注意第一个冒号左右边都已经超越了正下标的右限
b=a[7:100:1]#结果为空,等价于a[6:6:1],注意第一个冒号左右边都已经超越了正下标的右限
b=a[-6:6:1] #结果为python,而负下标的-6正好对应正下标0,所以等价于a[0:6:1];或全部转为负下标,等价于[-6:-1:1]
#当k>0时,可以将i,j全转换成正下标去理解。
b=a[-7:6:1] #结果为python,左闭右开,此处负下标越界,等价于a[-6:6:1]=a[0:6:1]
b=a[-100:6:1]#结果为python,注意-100已经超过了负下标的左限,等价于a[-6:6:1]=a[0:6:1]
b=a[-100:100:1]#结果为python,注意-100已经超过了负下标的左限,等价于a[-6:6:1]=a[0:6:1]
b=a[-6:-1:1]#结果为pytho,等价于a[0:5:1],注意,-6转换成正坐标为0,-1转换为正坐标为5.
b=a[-100:-1:1]#结果为pytho,注意-100已经超过了负下标的左限,等价于a[-6:-1:1]=a[0:5:1]
b=a[0:-1:1]#结果为pytho,等价于a[0:5:1]
b=a[0:-100:1]#结果为空,注意-100已经超过了负下标的左限,等价于a[0:-6:1]=a[0:0:1]
b=a[0:-6:1] #结果为空,等价于a[0:0:1]
b=a[0:-7:1] #结果为空,等价于a[0:0:1]
b=a[:j] #结果为pyth。k缺省(默认)为1,k大于0时,i缺省(默认)为0,j缺省(默认)为len(a)
b=a[i:] #结果为ython,表示从下标i开始到最后一个(下标为len(a)-1)
b=a[:] #结果为python,等价于a[0:6:1],表示从下标0开始到最后一个结束,步长为1。
b=a[::] #结果为python。等价于a[0:6:1]。a[i:j:k]中,k缺省为1,当k大于0时,i缺省为0,j缺省为len(a)。
b=a[::10] #结果为p。等价于a[0:6:10]。a[i:j:k]中,当k大于0时,i缺省为0,j缺省为len(a)
#当k<0是,可以将i,j全部转换成负下标去理解。
#k为负,表示从右往左顺次获取数组中的值,转换成负下标后,-len(a)-1 <= j < i <= -1才能获取到值。
b=a[i:j:-1] #结果为空,等价于a[1:4:-1]=a[-5:-2:-1]
b=a[-1:-7:-1]#结果为nohtyp,第一个冒号满足左闭右开原则。
b=a[-1:-100:-1]#结果为nohtyp,负下标越界,等价于a[-1:-7:-1]
b=a[4:0:-1] #结果为ohty,k为负数,将i,l转换成负下标理解,等价于a[-2:-6:-1],注意4转换成负下标为-2,0转换成负下标为-6
b=a[4:-1:-1]#结果为空,可以理解为a[-2:-1:-1]
b=a[4:-100:-1]#结果为ohtyp,k为负,将i转成负下标理解,同时j越界,等价于a[-2:-100:-1]=a[-2:-7:-1]
b=a[-1:0:-1]#结果为nohty,可以理解为a[-1:-6:-1]
b=a[0:-1:-1]#结果为空,可以理解为a[-6:-1:-1]
b=a[0:-2:-1]#结果为空 ,可以理解为a[-6:-2:-1]
b=a[-2:0:-1]#结果为ohty,可以理解为a[-2:-6:-1]
b=a[-1:6:-1]#结果为空,可以理解为a[-1:5:-1]=a[-1:-1:-1]
b=a[-1:100:-1]#结果为空,可以理解为a[-1:5:-1]=a[-1:-1:-1]
b=a[6:100:-1]#结果为空,可以理解为a[5:5:-1]=a[-1:-1:-1]
b=a[4:100:-1]#结果为空,可以理解为a[4:5:-1]=a[-1:-1:-1]
b=a[100:100:-1]#结果为空,可以理解为a[5:5:-1]=a[-1:-1:-1]
b=a[100:4:-1]#结果为n,可以理解为a[5:4:-1]=a[-1:-2:-1]
b=a[100:-100:-1]#结果为nohtyp,可以理解为a[5:-7:-1]=a[-1:-7:-1]
b=a[100:0:-1]#结果为nohty,可以理解为a[5:0:-1]=a[-1:-6:-1]
b=a[-100:100:-1]#结果为空,可以理解为a[-7:6:-1]=a[-7:-1:-1]
b=a[:-1] #结果为pytho ,等价于a[0:5:1]
b=a[::-1] #结果为nohtyp,等价于a[-1:-len(a)-1:-1] = a[-1:-7:-1]
插入
python中的list,tuple,dictionary 与numpy中的array mat是有区别的。
| String(字符串) | t = string | >>> t='Hello World!' | >>> t[0] |
| List(链表) | t = [value,value...] | >>> t={'abac', ”ggg”, 2,[1,2,3],(1,22,3)} | >>> t[0] |
| Tuple(元组) | t = (value,value...) | >>> t=('abac', ”ggg”, 2,[1,2,3],(1,22,3)) | >>> t[0] |
| Dictionary(字典) | t = {key1 : value1, key2 : value2} | >>> t = {'a': 1, 'b': 2, 'b': '3'} | >>> t['b'] |
| Set(集合) | t={value1,value2}或者 | >>>basket = {'apple', 'orange', 'apple', 'pear', 'orange', 'banana'} | >>> print(basket) # 这里演示的是去重功能 {'orange', 'banana', 'pear', 'apple'} >>> 'orange' in basket # 快速判断元素是否在集合内 True >>> 'crabgrass' in basket False |
| Numpy.array(数组) | t = [value,value...] value类型必须一致,要么都是数字,要么都是链表,要么都是字符串 | >>> t = np.random.rand(3,4) | >>> t [0.98119493, 0.36911137, 0.45306895, 0.09396056], [0.11345902, 0.17136475, 0.85474534, 0.56421904]]) |
| Numpy.mat(矩阵) | t = [value,value...] value类型必须一致,要么都是数字,要么都是链表,要么都是字符串。与array的区别在初始化与操作上的区别,需要可以去做相关搜索 或看 | >>> t = np.random.rand(3,4) | >>> t [0.98119493, 0.36911137, 0.45306895, 0.09396056], [0.11345902, 0.17136475, 0.85474534, 0.56421904]]) |
上面的各种类型中Dictionary 与Set 是不能通过数字下标访问的,Dictionary需要通过key来访问。
python3.7中只有numpy的array与numpy的mat才可以有多维数据的访问。
numpy中为方便矩阵操作更进一步使用了 “,” 和“...”符号(原生的python中只有一维数组操作, “,” 没有定义,无法像在numpy中那样通过 “,” 分隔来进行不同维度的操作)
在numpy 中上面操作的只是一个维度的操作描述,通过 “,” 来间隔不同维度的操作,如下
import numpy as np
pyArray=[['1','2','3','4','5','6'],['a','b','c','d','e','f']] #python的list类型
print(pyArray)
print(type(pyArray))
#print(pyArray[:,:3]) #TypeError: list indices must be integers or slices, not tuple #对python的list,tuple,array 操作时逗号被单纯的当做一个tuple,操作中没有意义
numpyArray = np.mat(pyArray) # 将python的list类型转换为numpy.ndarray类型。对python中的numpy中的mat或者array操作时,逗号用于作为不同维度的操作描述的间隔符。
print(type(numpyArray)) #numpyArray是个两行两列的mat。第一维以行为单位,有 2 个元素(这里元素为矩阵中的一行);第二维,以单独一行中的列为单位,这里第二维 有 6 个元素(这里元素为一行中的一个字符)
print(numpyArray[:,:3]) #获取所有行的前3列。
print(numpyArray)
#上面numpyArray[ : , :3 ]等价于numpyArray[ 0:2:1 , 0:3:1 ] 。 "," 前的部分 “0:2:1” 表示对第一维数据进行从0到2的步长为1的循环操作,并且每取一个元素都进行逗号后面的操作;
#"," 后的部分 “0:3:1” 表示对第二维数据进行从0到3的步长为1的循环操作。
输出结果如下:
[['1', '2', '3', '4', '5', '6'], ['a', 'b', 'c', 'd', 'e', 'f']]
<class 'list'>
<class 'numpy.matrix'>
[['1' '2' '3']
['a' 'b' 'c']]
[['1' '2' '3' '4' '5' '6']
['a' 'b' 'c' 'd' 'e' 'f']]a=[['1','2','3','4','5','6'],['a','b','c','d','e','f']] #定义二维数组,第一维就是两个子数组,也就是内部两个“[.....]”整体作为一个维度,这个维度中的元素为“[.....]”,并且每取一个元素都进行逗号后面的操作;第二维操作子数组中具体的内容,元素从第一维中取到的元素”[....]“中的具体某个字符,比如第一维取的元素['1','2','3','4','5','6'],那么第二维的元素有:'1','2','3','4','5','6';第一维取的元素['a','b','c','d','e','f'],那么第二维中的元素有:'a','b','c','d','e','f'。
更高维度的矩阵可以依此类推,通过逗号分隔不同维度的操作,进行级联。
a=np.array(a) #只有numpy中的array或者mat才对操作中的 “,” 起效用!!!!!!!!!!
b=a[:,0] #a[ : , 0 ]等价于[ 0:2:1 , 0 ]。操作中的 “,” 前面的 “:” ,表示对第一维数据进行步长为1的从下标0开始到下标2-1结束的逐个元素(行)遍历,并且每取一个元素都进行逗号后面的操作;“,” 后面的表示对第二维数据(第一维中取到的一行)只取第一个元素。结果为['1' 'a']。
b=a[::-1,:3] #a[ ::-1 , :3 ] 等价于[ 0:2:-1 , 0:3:1 ]。表示对第一维倒序,对第二维取前三个。结果为 下面的矩阵。![]()
b=a[::-1,::-1] #对两维的数据都取倒序。结果如下![]()
numpy中通过 “...” ,来处理高维度数据处理时的简写,所缩写的维度表示对该维度的所有元素逐个遍历一遍,相当于 0:size:1。
import numpy as np
print("--------1\n")
numpyArray1=np.random.rand(3,4,5) #生成一个numpy.ndarray类型的数据
print(numpyArray1)
a=numpyArray1[0,...,2] #对第一维只取第一个元素(下标从0开始),对第二维进行遍历,对第三维只取第三个元素
print("--------2\n")
print(a)
numpyArray1=np.random.rand(3,4,5,6)
print("--------3\n")
print(numpyArray1)
a=numpyArray1[0,...,2] #对第一维只取第一个元素(下标从0开始),对第二维进行遍历,对第三维进行遍历,对第四维只取第三个元素
print("--------4\n")
print(a)
测试结果
--------1
[[[0.75961301 0.26243631 0.1440737 0.24534408 0.31349595]
[0.79328679 0.590811 0.46102679 0.40292029 0.96344788]
[0.80784447 0.59973359 0.18902174 0.30202335 0.62644119]
[0.79960556 0.54618042 0.4891772 0.11393181 0.33576171]]
[[0.6945497 0.21748409 0.97254565 0.05819366 0.08903212]
[0.13094977 0.89284765 0.74385107 0.94299427 0.74814964]
[0.20090718 0.5080398 0.07829532 0.57883291 0.24903891]
[0.761288 0.88735529 0.54435107 0.56446666 0.74715601]]
[[0.1474583 0.84655107 0.1265764 0.11891323 0.00958817]
[0.58415654 0.20135703 0.77482195 0.61193237 0.89969648]
[0.4907176 0.74272329 0.74543795 0.23610179 0.65333147]
[0.76606038 0.23067704 0.42735718 0.75808523 0.00139425]]]
--------2
[0.1440737 0.46102679 0.18902174 0.4891772 ]
--------3
[[[[0.1812557 0.69170705 0.72024404 0.67798815 0.68197047 0.39215923]
[0.4444491 0.68557267 0.06645179 0.6045912 0.57379312 0.42740132]
[0.9917174 0.55845954 0.90794979 0.66427676 0.19494944 0.25205324]
[0.15963514 0.19172052 0.3905546 0.24775098 0.6326744 0.7240926 ]
[0.49168717 0.68135681 0.2798117 0.53264644 0.91745905 0.50570151]]
[[0.65818045 0.67643409 0.72921557 0.52120282 0.84265558 0.19478657]
[0.27173636 0.51248641 0.83054145 0.01243404 0.2286763 0.99442185]
[0.3942274 0.19094725 0.07536216 0.58963357 0.46108424 0.31990123]
[0.15946411 0.12185882 0.17107814 0.92633257 0.07676997 0.44995115]
[0.44220601 0.79271448 0.89496546 0.96422806 0.99068962 0.41112219]]
[[0.55634325 0.51426801 0.6869542 0.0220118 0.22800738 0.89283488]
[0.87644675 0.19170655 0.07371531 0.80521222 0.48763014 0.23803252]
[0.23822861 0.05605511 0.39511551 0.87032368 0.17964983 0.91669506]
[0.45564147 0.43596104 0.88526269 0.74199795 0.7009356 0.98035334]
[0.33038212 0.70477037 0.64018528 0.15233903 0.68263769 0.1726274 ]]
[[0.16103949 0.74056734 0.31915483 0.86233779 0.76993235 0.4778509 ]
[0.30610971 0.01805042 0.04392359 0.65439881 0.77759405 0.21863014]
[0.12050617 0.03656661 0.24780267 0.39592537 0.37356921 0.89682028]
[0.64333933 0.02194652 0.91047697 0.37407871 0.86987421 0.80684704]
[0.08526966 0.12471437 0.26344436 0.27125862 0.61027368 0.76130431]]]
[[[0.22824391 0.99362931 0.76669093 0.32020959 0.66995408 0.64363447]
[0.08629138 0.25151598 0.05031189 0.83360771 0.44522479 0.61706856]
[0.50244986 0.91878079 0.29809746 0.60595987 0.38759642 0.57423734]
[0.35077798 0.75415698 0.41718739 0.19202947 0.48746163 0.29919031]
[0.1547054 0.08591907 0.06909182 0.21636753 0.20477571 0.85270961]]
[[0.54275068 0.99823066 0.66857928 0.55803964 0.46994362 0.24384693]
[0.86382718 0.02783831 0.94782773 0.40242983 0.46016168 0.31866755]
[0.53234457 0.93043545 0.70298638 0.62500653 0.98193206 0.63179792]
[0.34040234 0.96194823 0.12764824 0.84721332 0.78953241 0.24072712]
[0.10481953 0.21080701 0.84852992 0.57694672 0.7579309 0.87596574]]
[[0.34702798 0.54355895 0.91389646 0.16613324 0.68964793 0.41555261]
[0.146322 0.95067996 0.58654328 0.91639038 0.98335253 0.52041599]
[0.08445805 0.91027324 0.88773413 0.23970592 0.48892042 0.73214968]
[0.7717916 0.25143908 0.74184745 0.20094771 0.49356631 0.59575285]
[0.8210064 0.00474716 0.21021144 0.77358007 0.29173552 0.14630372]]
[[0.80250384 0.59977446 0.44745813 0.96865905 0.22712192 0.30690933]
[0.68595101 0.6905422 0.4249482 0.14481983 0.75761848 0.67095763]
[0.38196093 0.51891229 0.24256184 0.40091079 0.25218622 0.68795537]
[0.09796337 0.18952714 0.85077095 0.10958704 0.89374984 0.71996563]
[0.83704889 0.40724607 0.04995298 0.54660527 0.52832754 0.30442538]]]
[[[0.06629056 0.94369297 0.32431709 0.46625179 0.25927881 0.7864168 ]
[0.92613301 0.80430149 0.43547641 0.81334823 0.21794206 0.85466773]
[0.06133655 0.18068038 0.90417705 0.50928607 0.0699663 0.04297818]
[0.81767779 0.64214533 0.73978392 0.11822394 0.2788445 0.41840177]
[0.19952065 0.38906961 0.48964289 0.07453175 0.83556159 0.44013533]]
[[0.30068616 0.10968057 0.47386595 0.502202 0.6253362 0.74100019]
[0.90587114 0.09874891 0.2775095 0.86033645 0.56380032 0.07740038]
[0.88257777 0.8785306 0.38717784 0.32747412 0.08440753 0.52961348]
[0.70838345 0.81444227 0.96959849 0.31217133 0.65446931 0.04904758]
[0.90227471 0.16703173 0.82468859 0.6725712 0.02499768 0.52484773]]
[[0.73779673 0.15129162 0.52397955 0.45160878 0.03180971 0.57787695]
[0.03531699 0.18233363 0.09853516 0.03732482 0.79312795 0.54557763]
[0.1430996 0.32698977 0.25119562 0.06159085 0.32735189 0.40050158]
[0.93599881 0.03526544 0.89073278 0.3948048 0.71796878 0.14900616]
[0.88732242 0.6499946 0.49507714 0.74056281 0.32381438 0.19796004]]
[[0.80766777 0.47538263 0.01639699 0.72943193 0.91251678 0.53546364]
[0.61515933 0.72301833 0.48649506 0.23785276 0.87192508 0.42441603]
[0.80488144 0.06195578 0.43105605 0.68724263 0.22095819 0.70886163]
[0.16173603 0.38668413 0.54902741 0.83016732 0.14687702 0.47873161]
[0.62618194 0.00281856 0.27227415 0.54113571 0.25803695 0.15752222]]]]
--------4
[[0.72024404 0.06645179 0.90794979 0.3905546 0.2798117 ]
[0.72921557 0.83054145 0.07536216 0.17107814 0.89496546]
[0.6869542 0.07371531 0.39511551 0.88526269 0.64018528]
[0.31915483 0.04392359 0.24780267 0.91047697 0.26344436]]更多推荐
 已为社区贡献1条内容
已为社区贡献1条内容







所有评论(0)