1、简介

$Sobel$ 本质是基于图像空间域卷积，卷积的作用除了实现图像模糊或者去噪，还可以寻找一张图像上所有梯度信息，这些梯度信息是图像的最原始特征数据，进一步处理之后就可以生成一些比较高级的特征用来表示一张图像实现基于图像特征的匹配，图像分类等应用。

$Sobel$ 算子是一种很经典的图像梯度提取算子，其本质是基于图像空间域卷积，背后的思想是图像一阶导数算子的理论支持。

$Sobel$ 算子主要用于获得数字图像的一阶梯度，常见的应用和物理意义是边缘检测。（$Laplacian$ 边缘检测并不局限于水平方向或垂直方向，这是 $Laplacian$ 与$Soble$ 的区别）

2、卷积

待处理的数字图像可以看做是一个大矩阵，图像的每个像素对应着矩阵的每个元素，假设我们的图像分辨率为 $1024\times 768$，那么对应大矩阵的的行数则为 $1024$，列数为 $768$.

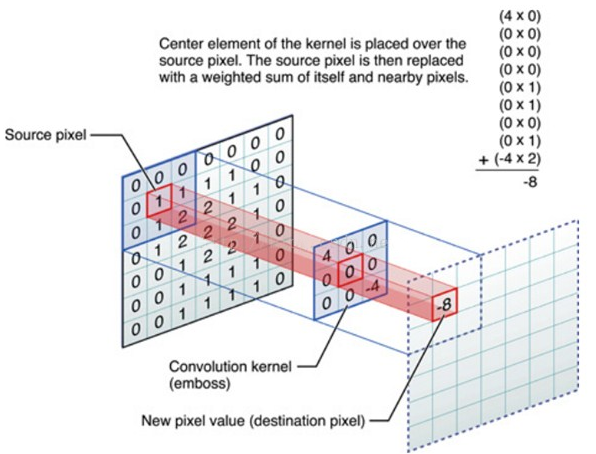
用于滤波（卷积核不止用于滤波）的小矩阵（也叫卷积核），一般是一个方阵，也就是行数和列数相同，比如常见的边缘检测 $Sobel$ 算子为 $3\times 3$ 的矩阵。

滤波就是对于大矩阵中的每个像素，计算它周围和滤波器矩阵对应位置元素的乘积，最后把乘积结果相加到一起，最终得到的值就作为该像素的新值。这样就对一个像素完成了一次滤波 。

3、Sobel 算子

该算子包含两组 $3\times 3$ 的矩阵，分别为横向及纵向，将之与图像作平面卷积，即可分别得出横向及纵向的亮度差分近似值。其公式如下：

Sobel 算子 X 方向：

$$G_x=\left[\begin{array}{ccc}-1& 0& 1\\ -2& 0& 2\\ -1& 0& 1\end{array}\right]\ast I$$

Sobel 算子 Y 方向:

$$G_y=\left[\begin{array}{ccc}-1& -2& -1\\ 0& 0& 0\\ 1& 2& 1\end{array}\right]\ast I$$

$$G=\sqrt{G_x^2+G_y^2}$$

$$G=|G_x|+|G_y|$$

Scharr 算子:

$$G_x=\left[\begin{array}{ccc}-3& 0& 3\\ -10& 0& 10\\ -3& 0& 3\end{array}\right]\ast I$$

$$G_y=\left[\begin{array}{ccc}-3& -10& -3\\ 0& 0& 0\\ 3& 10& 3\end{array}\right]\ast I$$

其中：

• $I$ 代表原始图像。
• $G_x$ 及 $G_y$ 分别代表经横向及纵向边缘检测的图像灰度值。
• $G$ 表示图像的每一个像素的横向及纵向灰度值，有两种计算方式。
• $Scharr$，比 $Sobel$ 算子的值更大，因此对于灰度变化更为敏感，会得到较强的边缘强度，但是也会损失一些细节。

如果想计算x方向梯度，我们就需要这样的一个卷积核：

$$G_x=\left[\begin{array}{ccc}-1& 0& 1\\ -2& 0& 2\\ -1& 0& 1\end{array}\right]\times \left[\begin{array}{ccc}{P}_1& P_2& P_3\\ P_4& P_5& P_6\\ P_7& P_8& P_9\end{array}\right]$$

4、Sobel 函数

$OpenCV$ 提供封装好的 $Sobel$ 算子函数：

cv2.Sobel(src, ddepth, dx, dy, ksize)

参数解释:

• src: 原图。
• ddepth: 处理结果图像深度，一般我们都填 $-1$，即与原图深度相同。但在这里我们需要填写 $cv2.CV\_64F$。简单来说就是如果填写 $-1$，我们在计算梯度时产生的负数就会被程序默认为 $0$，导致有一边的边缘出不来。而 $cv2.CV\_64F$ 范围更大，可以保留负数。
• d_x: 计算 $x$ 方向的梯度。
• d_y: 计算 $y$ 方向的梯度。
• ksize: 卷积核的尺寸。默认为 $3$，即 $3\times 3$ 的矩阵。

函数在使用时。如果我们想要计算 $x$ 方向的梯度：

cv2.Sobel(src, ddepth, 1, 0, ksize)

反之，计算 $y$ 方向的梯度

cv2.Sobel(src, ddepth, 0, 1, ksize)

当然，想要计算总梯度直接 $dx=1,dy=1$ 也是可以的，但是效果十分不好。不建议使用这种方法。
我们通常使用的方法是按权相加法。按权相加 $x$ 方向梯度和 $y$ 方向梯度。使用 $cv2.addWeight()$ 函数，该函数支持五个参数：

• src1: 第一幅图像
• weight1: 第一幅图像的权重
• src2: 第二幅图像
• weight2: 第二幅图像的权重
• 偏置值

我们还要注意一件事。在我们分别计算完 $x、y$ 方向的权值时，里面是有负数的。我们需要对这些负数取绝对值，否则照样会被归为 $0$。
取绝对值的函数是 $cv2.convertScaleAbs(img)$

import numpy as np
import cv2


img = cv2.imread('D://zopencv//qi.jpg', 0)
mask_x = cv2.Sobel(img,cv2.CV_64F, 1, 0)  # 计算x方向梯度
mask_y = cv2.Sobel(img,cv2.CV_64F, 0, 1)
img_x = cv2.convertScaleAbs(mask_x)  # 取绝对值
img_y = cv2.convertScaleAbs(mask_y)
mask = cv2.addWeighted(img_x, 0.5, img_y, 0.5, 0)  # 按权相加
# mask = cv2.Sobel(img,cv2.CV_64F,1,1)
Archie = cv2.resize(mask, None, fx=0.5, fy=0.5, interpolation=cv2.INTER_AREA)  # 图片太大了，缩小图片
cv2.imshow('Archie', Archie)
cv2.waitKey(0)
cv2.destroyAllWindows()