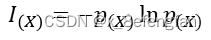
熵权法计算评价指标权重——使用Python和Excel实现
目录
问题提出
善始者繁多,克终者盖寡。
在学习的过程中遇到了这么一个问题:已经通过查阅资料确定了某个因变量受到好几个自变量的影响,可是不同的自变量对因变量的影响程度肯定不同,那这个时候不太能自变量对因变量的影响程度如何确定呢?换句话说就是各指标的权重是多少?
使用一个形象的例子来说明:假设已经通过查阅资料确定,一个人的气质受到身高、体重、年龄三个因素的影响,那么我们期望得到这么一个等式。
W=aX1+bX2+cX3
X1、X2、X3分别代表身高、体重、年龄三个指标;W表示气质的量化分数
一、熵权法
用来确定评价体系中各指标权重的方法大抵可以分为三类:经验的方法,数学的方法以及两者混合的方法。常见的经验方法有层次分析法、模糊层次分析法、德尔菲法等;常见的数学方法有熵权法、离差法等。
熵权法是从信息量的角度判断各指标权重大小的。
不同指标的变化必定引起测量目标的变化,变化程度越大,说明该指标的影响越大,其占据的权重也应当大。
说到信息量就不得不提到信息论奠基人香农及其相关理论。
1.1 信息量与信息熵
关于信息量及信息熵的详细描述可以参考这位博主转载的文章。
信息熵
信息量很好理解,它反映的是某个时间所包含的信息的多少,即信息量越大其包含的信息越多,事物的不确定越小;信息熵则是对事物不确定性的描述,熵越大表示事物的不确定性越高,其包含的信息越少,熵越小表示事物的不确定性越小,其包含的信息越多。
熵反映了事物的不确定性,熵越小,事物的不确定性越小,其能够提供的信息越多。
1.2 信息量与信息熵的计算
信息量的多少可以通过事物发生的概率反映出来,一件事情发生的概率越高,其包含的信息量越大,信息量的计算公式为:

p(X)表示事件X发生的概率;I(X)表示事件X包含的信息,其结果是[0,1]的某个值。
至于为什么用对数函数,已经有大量研究说明了。
通过信息量我们可以来描述系统的不确定性,即熵,熵的计算公式为:

n表示系统中事件的个数;p(Xi)表示系统中的每一个事件发生的概率;H(X)表示系统的信息熵,取值范围仍为[0,1],其取值越大表明系统不确定性越大,包含的信息越少。
熵权法是根据各指标的熵值来判断指标权重的,指标包含的信息越多,其占据的权重应当大,即越是重要的指标,其熵值越小。
1.3 熵权法的计算
我们使用信息熵的计算公式就能够计算出每一个指标(列)的熵,其计算公式为:
 我们可以发现,每一个指标(列)熵的计算公式就是在信息熵计算公式前加了一个“ln(x)”,那这个“ln(x)”表示什么呢?
我们可以发现,每一个指标(列)熵的计算公式就是在信息熵计算公式前加了一个“ln(x)”,那这个“ln(x)”表示什么呢?
从数学角度看,当所有事件发生概率相同时,系统信息熵最大,其值为ln(x),为了保证我们计算出来的数值在[0,1]内,我们在前面除以ln(x)
但是请注意,我们此时计算出来的只是某一个指标(列)的熵,熵反映的这个指标的不确定性,我们使用“信息效用”来表示该指标包含的信息量,信息效用的计算公式为:
d=1-H(x)
d表示该指标包含的信息量,值越大说明其包含的信息越多;H(X)是先前计算出的指标的熵,
使用相同的方法依次计算出每一指标的熵及其信息效用,再计算当前指标在所有指标中的比重,即当前指标在系统中的权重。假设W=[w1,w2…,wm],m表示系统中指标的个数,wi表示第i个指标的权重;H=(h1,h2…,hm),hi表示第i个指标的信息熵;D=(d1,d2…,dm),di表示第i个指标的信息效用,各指标权重的计算公式表示为:

二、使用Excel计算指标权重
假设已通过查阅文献资料确定气质由身高、体重、年龄三个因素影响,并收集到了5名背时的相关信息。

2.1 数据归一化
归一化的目的是消除量纲的影响。
“身高”的单位是cm;体重的单位是kg;年龄的单位是岁。使用原始数据可能会过分放大某一指标对最终结果的影响,例如假设最终求得“身高”和“年龄”的权重都为0.5,那么最终得分高低肯定是由“身高”主导的,因为大头在“身高”这边。
常用的数据归一化方法为极差法,计算公式为:

Xi表示当前数据;Ci表示当前数据归一化后的结果,其取值范围为[0,1];min(X)、max(X)分别表示当前指标中的最小值与最大值。
以A2单元格为例,数据归一化的计算公式为:
=(A2-MIN(A$2:A$6))/(MAX(A$2:A$6)-MIN(A$2:A$6))
归一下后数据变为:

2.2 计算各记录信息熵
根据信息熵计算公式,求得每一个单元格中数据的信息熵:
注意:此时概率表示为:p=当前数据值/该列数据总和
以A2单元格为例,其计算公式为:
=E2/SUM(E$2:E$6)LOG(E2/SUM(E$2:E$6))-1
依次计算所有单元格的信息熵,结果为:
 各单元格的信息熵计算完毕后可以计算每一个指标的总熵,以“身高”为例,其计算公式为:
各单元格的信息熵计算完毕后可以计算每一个指标的总熵,以“身高”为例,其计算公式为:
=SUM(I2:I6)/LOG(5)
注意:此时记录中仅包含5条数据,所有使用LOG(5),对于记录较多的数据可以使用count函数代替
“身高”的权重计算公式为:
=(1-I8)/(3-SUM($I 8 : 8: 8:K$8))
注意:此时分母中的3为指标的个数,可以使用count函数代替;各指标权重和为1
最终三指标的权重分别为:

根据计算出的权重重新计算每一条记录的最终得分,结果为:

三、使用Python计算指标权重
3.1 读取Excel文件
本人习惯于将需要用到的数据集存放在同级目录“files”下,保持一份数据底稿用以计算每条记录最终得分。
import pandas
import math
filename = "示例信息熵.xlsx"
path = "files/"
data = pandas.read_excel(path+filename,sheet_name=0)
#保留原始数据
data_yuanshi = data.copy()
print(data)
3.2 归一化化数据
使用2.1提到的极差法将数据归一化,同时也保存一份归一化后的数据。
max = data.max()
min = data.min()
cols = data.columns
#归一化数据
for i in range(data.shape[0]):
for j in range(data.shape[1]):
data.iloc[i,j] = (float(data.iloc[i,j])-float(min[cols[j]]))/(float(max[cols[j]])-float(min[cols[j]]))
data_guiyi = data.copy()
print(data)
3.3 计算每条记录的信息熵
需要注意的是,在计算0*LOG(0)是程序会报错,所以需要进行特殊处理。
#存储每一条记录的熵
result_sum_col = []
for j in range(data.shape[1]):
sum_col = data[cols[j]].sum()
# print(sum_col)
for i in range(data.shape[0]):
if data.iloc[i,j] == 0:
#计算Log(0)是会报错,需要特殊处理
data.iloc[i, j] = 0
else:
data.iloc[i,j] = -1*(data.iloc[i,j]/sum_col)*math.log10((data.iloc[i,j]/sum_col))
#该指标的熵等于各记录熵的和除以Log(n),n为记录的条数
result_sum_col.append(data[cols[j]].sum()/math.log10(data.shape[0]))
# print(result_sum_col)
print(data)
3.4 计算各指标的权重
根据信息熵、信息效用的计算公式计算出指标的权重,将其存储起来。
weight = []
weight_sum = 0.0
for i in result_sum_col:
weight_sum += i
'''
i表示各个维度的熵,n表示维度的个数
各维度计算公式为(1-i)/(n-sum_i)
'''
for i in result_sum_col:
weight.append((1-i)/(float(data.shape[1])*1-weight_sum))
print(weight)
3.5 计算每条记录最终得分
#计算各记录最终得分并另存文件(原始数据文件)
cores = []
for i in range(data_yuanshi.shape[0]):
result_core = 0
for j in range(data_yuanshi.shape[1]):
result_core += float(data_yuanshi.iloc[i,j])*weight[j]
cores.append(result_core)
print(cores)
data_yuanshi["最终评分"] = cores
print(data_yuanshi)
#计算各记录最终得分并另存文件(归一化数据文件)
cores2 = []
for i in range(data_guiyi.shape[0]):
result_core = 0
for j in range(data_guiyi.shape[1]):
result_core += float(data_guiyi.iloc[i,j])*weight[j]
cores2.append(result_core)
print(cores2)
data_guiyi["最终评分"] = cores2
print(data_guiyi)
3.6 保存文件
本人将最终计算出的指标权重放在“熵.xlsx”表中,程序运行后会生成三份文件。
'''
熵文件中不用计算最终得分,但要写入指标权重
'''
data.loc["权重"] = weight
print(data)
#保存文件
file01 = filename.split(".")[0]+"最终得分.xlsx"
file02 = filename.split(".")[0]+"归一化.xlsx"
file03 = filename.split(".")[0]+"熵.xlsx"
data_yuanshi.to_excel(path+file01,index=False)
data_guiyi.to_excel(path+file02,index=False)
data.to_excel(path+file03)
程序运行结果效果图为:



从运行结果1、2图可以看出归一化的效果。
记录2规约化后最终得分高于记录5,但是!!!在原始数据中记录5最终得分却高于记录2,因为原始数据三个指标量纲不同。
更多推荐
 已为社区贡献1条内容
已为社区贡献1条内容









所有评论(0)