重心法模型介绍

        重心法的基本原理是把各个物流需求点看作存在一个平面内，再将每个需求点的需求量当作物体的质量，算出该物体系统的物理重心，即物流配送中心。重心法将待求点的位置坐标看成变量，放在平面直角坐标系中，然后表示出待求点与需求点之间的理论距离，再将该距离分别与需求量、运费相乘的乘积之和作为需求函数，计算出函数的最小值即可。

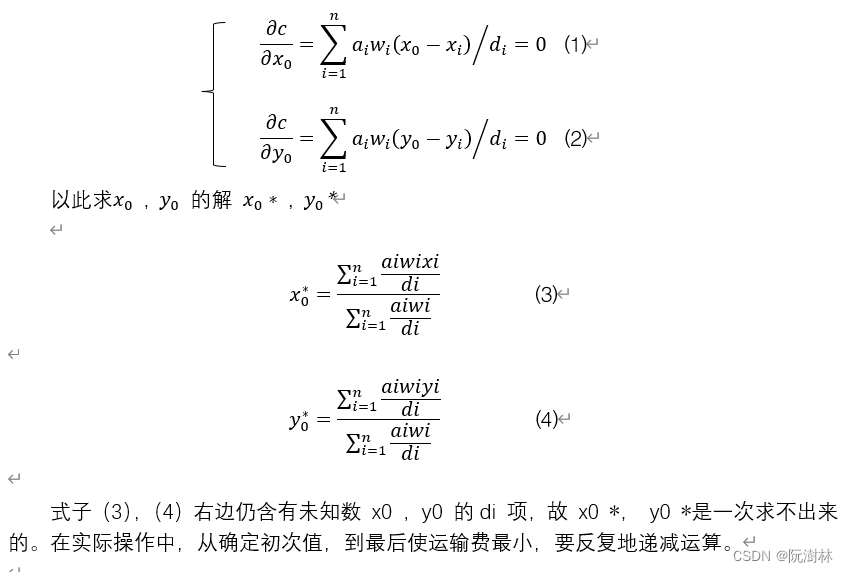
设有 n 个供给区域点，这些供给点的坐标为(Xi，Yi)，假设逆向物流回收中心设置在(X0，Y0)处。总运输成本表示为 C：

                                                  

式中：ai ——指从供给点 i 到回收中心单位距离单位重量所需运输成本；

      wi ——指回收中心到供给点 i 的运输量；

      di ——指回收中心到供给点的距离， 

要想使求得总费用C最小的方法是根据 一阶偏导数为零的原理求解的,因此令

重心法模型的改进

       在传统重心法中，需求点到待求点的距离是用直线来代替的, 由于这样误差比较大，所以引入非直线系数 Ci，非直线系数能够将需求点到待求点的直线距离 di转换成运输距离 Di，与现实情况会更相近。

重心法模型的建立

建立模型的准备工作包括以下几个方面：

第 1 步：根据经验或者企业的要求，确定要进行选址的地区，初次确立的地区范围往往比较大，将其划分为更小的需求点，这个需求点需要缩小范围，统计这些需求点的个数。

 第 2 步：运用GIS地理信息系统查询每个需求点的具体经纬度坐标，选取合适的坐标原点建立平面直角坐标系，例如以经纬度作为参考坐标系。将每个地点的名称输入地理信息系统查得其经纬度。

第 3 步：确定各需求点对物资的需求量即（运输量），确定各需求点运输该物资时需要的运输费用。运输费用一般都不固定，会根据其他的某些因素而产生变化，假设在某一段时间，商品的运输费用不会发生变化。

第 4 步：求初始解，假设在选址过程中，存在 n 个需求点，令这些需求点的坐标为 （Xi ,Yi），需求量分别为 Wi（i=1,2,3,…,n）。待求的循环产业园位置，最优位置坐标为（x0 ∗， y0 ∗）；ai为待求点到各个需求点 i 的运输费率，使用传统重心公式求出循环产业园的初始坐标  。

第 5 步：通过迭代求得最优解。将求得物流中心的初始坐标代入式（6）、（7），计算出运输距离 Di和总费用 C；将 Di代入式 （8），求出改善后的物流配送中心坐标 （Xi ,Yi） ；重复以上计算过程，直到计算出的总运输成本C最小。

第 6 步：初步确立物流中心位置。本文用matlab软件对模型进行计算，在matlab软件上根据上述步骤编写代码，经过数次迭代之后计算出坐标值和最小运输费用，利用地理信息系统查询经纬度坐标，能够查询到该坐标值对应的实际位置。根据现实状况，对该坐标值区域一定范围进行考察，最终确定物流中心布局位置。

重心法例子演示及相关matlab代码

      建立重心法模型

      首先确定初始范围和需求点，这个根据碰到的实际问题而定，本文例子皆是假设并且以经纬度作为参考坐标系，假定有3个需求点需要物流中心进行配送，3个需求点的经纬度坐标分别为（30.5，120.5），（26.2，117.5），（28.5，116）。然后确定各需求点的运输量和运输费率，在实际问题中需要对相关需求点进行调研，根据现实情况而定，这里假定3个需求点运输量分别为248700吨，180500吨，100000吨。运输费率这里为了简化模型统一设运输费率为0.6。最后确定非直线系数，由于各地交通道路情况不同，对于不同地区的合理非直线系数也不相同，这里假设非直线系数为1.5。

     计算模型

在确定好模型各个变量参数后，使用matlab软件对模型进行编码并计算。下面为matlab代码。

clc;clear;

d = [];%初始化变量，表示物流中心与各节点距离

D = [];

X = [30.5,26.2,28.5]; %各节点横坐标

Y = [120.5,117.5,116]; %各节点纵坐标

V = [248700,100000,180500]; %各节点运输量

f = [0.6,0.6,0.6]; %各节点运输费率

t = 0; %记录算法迭代次数

for i = 1:3

    %%计算初始位置坐标

    z1(i)=f(i)*V(i)*X(i);

    z2(i)=f(i)*V(i);

    z3(i)=f(i)*V(i)*Y(i);

end

x0=sum(z1)/sum(z2);

y0=sum(z3)/sum(z2);

x = x0; %初始点横坐标

y = y0; %初始点纵坐标

for k = 1:1000 %设置迭代次数

s1 = 0;

s2 = 0;

s3 = 0;

sco = 0;

scn = 0;

transport = 0;

Ci = 1.5; %非直线系数Ci

for i = 1:3

d(i) = sqrt((x-X(i))^2+(y-Y(i))^2); %计算直线距离

D(i) = Ci*d(i)

sco = sco + f(i)*V(i)*D(i); %费用的求和计算

s1 = s1 + X(i)*f(i)*V(i)/D(i); %迭代公式横坐标分子

s2 = s2 + Y(i)*f(i)*V(i)/D(i); %迭代公式纵坐标分子

s3 = s3 + f(i)*V(i)/D(i); %迭代公式分母

end

x = s1 / s3;

y = s2 / s3;

for i = 1:3

d(i) = sqrt((x-X(i))^2+(y-Y(i))^2); %新的坐标与各节点的距离计算

D(i) = Ci*d(i)

scn = scn + f(i)*V(i)*D(i); %迭代的总运输费用

end

if sco <= scn %判断是否满足迭代结束条件

transport = transport + sco; break; %判定是否为迭代当前最小运输费用

end

t = t + 1;

end

t%输出迭代次数

x%输出物流中心的横坐标

y %输出物流中心的纵坐标

transport %输出最小运输费用

        如上图，经过数次迭代计算后得到了经纬度坐标（29.1，118.45），即北纬29.1度，东经118.45度为重心法计算得出的选址区域。算得最小运输费用约为124万元。 

重心法模型分析

       重心法模型运输成本计算采用的是简单的线性函数，但是在实际操作中，派出一趟车，就要产生费用，不管车子是否满载及距离的大小。在计算边际费用的时候，物流中心的管理成本中的固定费用部分也忽略不计。这会大大地降低模型的有效性。

       从供给区域点到需求点，在计算距离的时候都不能使用直线距离来计算。优化后的重心法模型引入非直线系数Ci来使计算距离更合理。从全局来看，重心法模型是一个连续的选址模型，所以地点的选择是没有限制的，但是最终的计算结果得到的地点很可能实际上不符合物流中心建设需求。例如最终建设地点处于山川河流中，因此建议使用重心法进行初步选址，用重心法求出坐标后，还需对求得地点进行进一步考察。

       重心法的优点是：备选地点是连续的选择没有限制在某些位置上，比较灵活，在计算上重心法也很简单，问题通过重心法描述也很直观容易理解。这个模型最大的特点就是备选地点不被限制可以在平面内自由的选址。对于单个及多个回收中心的求解计算都能使用此模型。