“傻瓜”学计量——平行趋势检验 (看完就会)
提纲:
1.什么是平行趋势假设?为什么要满足平行趋势假设?
2.怎么做平行趋势检验?
2.1.传统双重差分法的平行趋势检验
2✖2传统DID 无法 做平行趋势检验
2.2.多时点DID的平行趋势检验
2.2.1绘图
2.2.2.回归模型
2.3.多期DID的平行趋势检验
2.3.1. 双重固定效应模型
2.3.2.CSDID
1.平行趋势检验
1.1.平行趋势检验的假设
如果没有处理行为,处理组与非处理组(对照组)的平均结果有相同的发展趋势。
注意:并不是直接作用于处理行为发生之前的,也不是要求处理行为发生之前的两组变化趋势相同。针对的是处理行为发生之后。由于处理行为发生之后的反事实结果,也就是处理组,没有接受处理行为的结果,我们无直接观测到,所以采用处理行为发生之前的趋势对处理行为发生之后的趋势做一个预测。
2.怎么做平行趋势检验?
2.1.传统双重差分法的平行趋势检验
2✖2传统DID 无法 做平行趋势检验
2.2.多时点DID的平行趋势检验
多时点双重差分法可以,方法有二:绘图、回归。(若只能选一个,则选回归。)
2.2.1.绘图
2.2.1.1.如何从图中看出是否通过平行趋势检验
画出处理组和非处理组效应对象(Y)在每个时间里的平均值。最终图像如下:

我们要关注:处理行为发生之前的这个时间段,即上图绿框中的部分。关注处理行为发生之前,处理组与非处理组的走势是否相同。由于绿框中两组走势相似,因此,我们就说这个数据大概率满足平行趋势假设。
2.2.1.2.绘制方法
| 步骤 | 含义 | 小步骤 | stata指令 | 指令解释 |
| 第一步 | 计算每个组别,每个时间点效应对象的平均值 | 1 | sort 第一个排序变量组别 第二个排序变量时间 | 根据组别和时间给数据排序 |
| 2 | by 组别变量 时间变量 : egen 新变量名称 = 计算方法 | 根据组别和时间 生成 变量:每一个组别每个时间点的体重平均值 | ||
| 第二步 | 根据平均值绘图 | 3 | twoway (connected 输入点的纵坐标变量名 输入点的横坐标的变量名 if 处理组名称==1) (connected 输入点的纵坐标变量名 输入点的横坐标的变量名 if 处理组名称==0) ,legend(label(1 “treated") label(2 "untreated")) xline(5) xscale(range(1 12)) xlabel(1 (1) 12) | twoway画一个有xy坐标的二维图; () ()图上有两条线; connected画一条直线,这条直线是通过一些点来连接的折线图; ==进行一个语句判断; ==1:只有在处理组取到1时,才绘制第一个折线图; ==0:只有在处理组取到0时,才绘制第二个折线图; 以上是绘制图像👆 以下是让图更美观👇 legend :说明标识 label:标签 1 “treated":告诉stata第一条线是处理组 2 "untreated":告诉stata第二条线是非处理组 绘制垂直的红线,说明处理行为发生的时间节点。 xline:绘制垂直的直线 5:表示在横坐标为5的位置画一条垂线 x的取值范围及取值区间 xscale(range(1 12)):x的取值范围是1-12 xlabel(1 (1) 12):x轴的取值间距是1 |
2.2.1.3.绘图法缺点
| 无法得出明确的结论,即绿框范围中只能凭肉眼看是否趋势相同,无法量化 |
| 无法添加控制变量,有可能导致处理行为前的部分不准确,有可能受到遗漏变量的影响 |
2.2.2.回归模型
2.2.2.1.原理:
| 经典回归模型 | 多时点DID平行性趋势检验的模型 |
|
👇
| |
|
| 关注,上述红框中的交乘项系数是否显著区别于零: 若都不显著,则我们说数据通过了平行趋势检验; 若大于等于1个显著,则我们说数据没有通过平行趋势检验。 |
2.2.2.2.stata处理方法
| 步骤 | 含义 | stata指令 | 指令解释 |
| 1 | 生成一个新的变量 | tab 时间变量名称,gen(希望得到的变量名) | tab 时间变量名称:时间变量名的频数 gen(希望得到的变量名):生成一个新的变量 |
| 2 | 浏览数据 | br | |
| 3 | 生成交乘项 | gen 交乘项的名称=模型中D的变量名称*第1 步中希望的得到的变量名 | 只得到了一个交乘项 |
| 4 | 生成其他交乘项 | ||
| 5 | xtset 面板的个体识别变量 时间识别变量 | 面板数据用固定效应模型回归 xtset:告诉stata我们的数据是面板数据 | |
| 6 | 回归 | xtreg 因变量 所有组别交乘项(处理行为发生之前的那一组交乘项要剔除) i.month,fe | xtreg:回归命令 i.month:时间固定效应 fe:个体固定效应 |
如果处理时间之前的组别t值都接近于零,不显著;回归系数也非常小,即经济意义不显著,
此时,我们就说数据结果通过了平行性趋势检验。
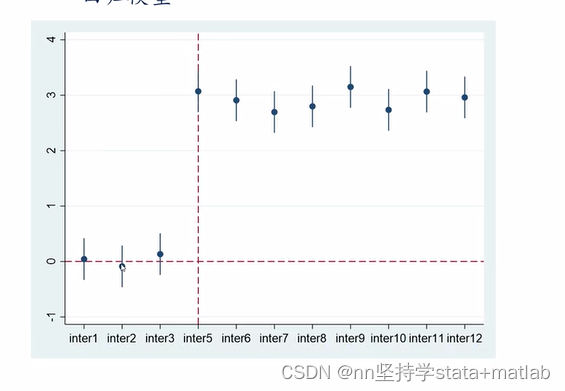
2.2.2.3.文献中平行趋势检验常见图
(1)图解读

| 点 | 对应交乘项的系数 |
| 点上下的小竖线 | 交乘项系数所对应的置信区间 |
前三个点交乘项系数的置信区间都覆盖0,则他们都不显著区别于0,则通过平行趋势检验。
(2)stata画图步骤
| 步骤 | stata指令 | 指令解释 |
| 1 | ssc install coefplot | 安装外部指令 ssc install:安装外部指令 coef:coefficient系数的缩写 plot:图像 |
| 2 | 平行趋势检验回归模型 | 详见 上个表格步骤6 |
| 3 | coefplot, keep(交乘项总称*) vertical yline(0,lp(dash)) xline(4,lp(dash)) | keep:需要绘制那些因变量的系数结果 *:表示要保留所有以交乘项总称开头的变量 👇
和上图不同,还需继续修改 vertical:让所有的置信区间垂直放置 yline(0:在y轴0点处画一条水平的虚线 lp:决定线的形状 dash:虚线 xline:在x轴处画一条垂直的线 (4):inter5是x轴的第四个取值 即可得:
|
2.3.多期(处理行为发生时间不同)DID的平行趋势检验
2.3.1. 双重固定效应模型TWFEDD
(1)原理
| 双向固定效应模型TWFEDD | 多期did平行趋势检验的模型 |
|
👇
| |
|
| 进行平行趋势检验,主要关注红框中的内容,即处理行为发生之前的时间点的系数是否显著。(原理同多时点DID检验相同。) |
(2)stata操作步骤
| 步骤 | stata指令 | 指令解释 | ||
| 1 | edit | 打开stata中类似于excel表格的部分,将数据粘贴进来,之后关闭数据 | 导入数据 | |
| 2 | gen relative_period= month - treatment_time if treatmentgroup==1 | 计算每一个观测值所在时间点,与处理行为发生时间点,的距离是多少 relative_period:要生成的新变量的名称 month:这一个观测值所在的时间点 treatment_time:处理行为发生的时间点 if treatmentgroup==1:只对处理组进行计算 stata显示:600 missing value generated 指的是有600个缺失值,这里对应的是非处理组的观测值缺失 | 生成一个新变量relative _period | 生成0-1变量 |
| 3 | replace relative_period=999 if relative_period==. | ==.:假如是缺失值 999:随意赋值一个较大的数 replace:赋值 | ||
| 4 | tab relative_period,gen(dummy) | 生成0-1变量 | ||
| 5 | xtset uid month | xtset:面板数据 uid:个体标识变量 month:时间标识变量 | 面板数据 | |
| 6 | xtreg weight d1 d2 d3 d4 d5 d6 d8 d9 d10 d11 d12 d13 d14 d15 i.month,fe | xtreg:回归 weight:因变量 d1 d2 d3 d4 d5 d6 d8 d9 d10 d11 d12 d13 d14 d15:自变量,即刚刚生成的一组0-1变量,但不包含处理行为发生前一期 i.month:时间固定效应 fe:个体固定效应 | 回归 | |
| 7 | coefplot, keep(d*) vertical yline(0,lp(dash)) xline(7,lp(dash)) | 7:处理行为发生当期,即D8这个0-1变量,是我们绘图当中的第7个变量 | 绘图 | |
2.3.2. CSDID平行趋势检验
| 种类 | stata指令 | 指令含义/方法 |
| 对每个组别进行平行趋势检验 | csdid weight,ivar( uid ) time ( month ) gvar( treatment_time ) | 针对每一个组别进行的。主要看,发生当期之前的几期,的系数是否显著接近于零。若不然,则每个组别的平行趋势检验不通过。 |
| 对总体进行平行趋势检验 | 1.csdid回归 2.estat pretrend 👇
| 卡方检验 原假设H0:所有处理行为发生前的小模块的系数全为0。 备择假设:至少有一个处理行为发生前的小模块是显著区别于0的。 👇 因为p值远远小于0.05,则至少有一个小模块的系数是显著不等于0的,那我们的平行趋势检验不能通过。只有当p值大于0.05时,才能通过平行趋势检验。 |
资料来源:up主 小周同学慢慢学
墙裂推推荐~小周老师讲的非常细非常好懂,她声音超好听,而且很幽默偶~
更多推荐
 已为社区贡献4条内容
已为社区贡献4条内容















所有评论(0)