一、多项式拟合

• ployfit(x,y,n) ：找到次数为 n 的多项式系数，对于数据集合 {(x_i,y_i)}，满足差的平方和最小
• [P,E] = ployfit(x,y,n) ：返回同上的多项式 P 和矩阵 E 。多项式系数在向量 p 中，矩阵 E 用在 ployval 函数中来计算误差
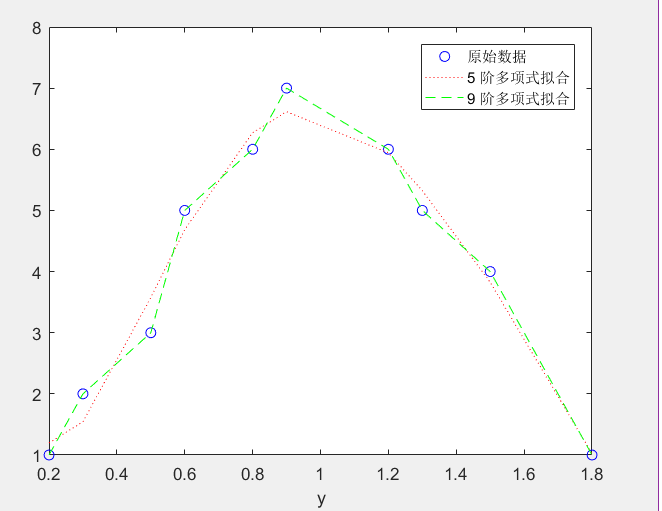
• 某数据的横坐标为 x= [0.2 0.3 0.5 0.6 0.8 0.9 1.2 1.3 1.5 1.8]，纵坐标为 y = [1 2 3 5 6 7 6 5 4 1]，对该数据进行多项式拟合
• 代码

      clear all
      clc
      x = [0.2 0.3 0.5 0.6 0.8 0.9 1.2 1.3 1.5 1.8];
      y = [1 2 3 5 6 7 6 5 4 1];
      p5 = polyfit(x,y,5);				 % 5 阶多项式拟合 
      y5 = polyval(p5,x);
      p5 = vpa(poly2sym(p5),5)			 %显示 5 阶多项式
      p9 = polyfit(x,y,9);				 % 9 阶多项式
      y9 = polyval(p9,x);
      figure;								%画图
      plot(x,y,'bo');
      hold on;
      plot(x,y5,'r:');
      plot(x,y9,'g--');
      legend('原始数据','5 阶多项式拟合','9 阶多项式拟合');
      xlabel('x');
      xlabel('y');

• 运行程序后，得到的 5 阶多项式如下：
  p5 =10.041x^5 + 58.244x^4 - 124.54x^3 + 110.79x^2 - 31.838*x + 4.0393

• 输出结果如下：

  

• 可见，当采用 9 次拟合时，得到的结果与原数据符合的比较好。当使用函数 polyfit() 进行拟合时，多项式的阶次最大不超过 length(x) - 1

二、加权最小方差(WLS)拟合原理及实例

• 加权最小方差就是根据基础数据本身各自的准确度的不同，在拟合的时候给每个数据以不同的加权数值。这种方法比单纯最小方差方法要更加符合拟合的初衷
• 根据 WLS 数据拟合方法，自行编写使用 WLS 方法拟合数据的 M 函数，然后使用 WLS 方法进行数据拟合
• 在 M 文件编辑器中输入如下代码：

      function [th,err,yi] = polyfits(x,y,N,xi,r)
      % x，y：数据点系列
      % N：多项式拟合的系统
      % r：加权系数的逆矩阵
      
      M = length(x);
      x = x(:);
      y = y(:);
      
      % 判断调用函数的格式
      if nargin == 4
      % 当调用的格式为 (x,y,N,r)
      	if length(xi) == M
        		r = xi;
        		xi = x;
      % 当调用的格式为(x,y,N,xi)
       	else r = 1;
       	end;
      % 当调用格式为(x,y,N)
      elseif nargin == 3
      	xi = x;
      	r = 1;
      end
      % 求解系数矩阵
      A(:,N+1) = ones(M,1);
      for n = N:-1:1
      	A(:,n) = A(:,n+1).*x;
      end
      if length(r) == M
      	for m =1:M
      		A(m,:) = A(m,:)/r(m);
      		y(m) = y(m)/r(m);
      	end
      end
       % 计算拟合系数
      th = (A\y)';
      ye = polyval(th,x);
      err = norm(y-ye)/norm(y);
      yi = polyval(th,xi);

• 将上面代码保存为 “polyfits.m” 文件
• 使用上面的程序代码，对基础数据进行 LS 多项式拟合。在 MATLAB 的命令窗口输入下面的程序

     clear all
      clc
      x = [-3:1:3]';
      y = [1.1650 0.0751 -0.6965 0.0591 0.6268 0.3516 1.6961]';
      [x,i] = sort(x);
      y = y(i);
      xi = min(x) + [0:100]/100*(max(x) - min(x));
      for i = 1:4
      	N = 2*i-1;
      	[th,err,yi] = polyfits(x,y,N,xi);
      	subplot(2,2,i)
      	plot(x,y,'o')
      	hold on
      	plot(xi,yi,'-')
      	grid on
      end

• 得到的拟合结果

  

• LS 方法其实是 WLS 方法的一种特例，相当于将每个基础数据的准确度都设为 1。但是，自行编写的 M 文件和默认的命令结果不同

• matlab计算曲线拟合度的程序 MATLAB曲线拟合向导

三、非线性曲线拟合

• 非线性曲线拟合是已知输入向量 xdata，输出向量 ydata，并知道输入与输出的函数关系为 ydata = F(x,xdata)，但不清楚系数向量 x。进行曲线拟合急求 x 使得下式成立：
  \(\displaystyle{min_x} \frac{1}{2}|| F(x,xdata)-ydata||_2^2 = \frac{1}{2}\displaystyle{\sum_i}(F(x,xdata_i) - ydata_i)^2\)
• 在 MATLAB 中，可以使用函数 curvefit 解决此类问题，其调用格式如下：
  • x = lsqcurvefit(fun,x0,xdata,ydata)：x0 为初始解向量，xdata，ydata 为满足关系 ydata = F(x,xdata)的数据
  • x = lsqcurvefit(fun,x0,xdata,ydata,lb,ub)：lb、ub 为解向量的下届和上届 lb <= x <= ub，若没有指定界，则lb = []，ub = []
  • x = lsqcurvefit(fun,x0,xdata,ydata,lb,ub,options)：options 为指定的优化参数
  • [x,resnorm] = lsqcurvefit(…)：resnorm 是在 x 处残差的平方和
  • [x,resnorm,residual] = lsqcurvefit(…)：residual 为在 x 处的残差
  • [x,resnorm,residual,exitflag] =lsqcurve(…)：exitflag 为终止迭代的条件
  • [x,resnorm,residual,exitflag,output] =lsqcurve(…) ：output 为输出的优化信息
• 已知输入向量 xdata 和输出向量 ydata，且长度都是 n，使用最小二乘非线性拟合函数：ydata(i) = x(1)·xdata(i)^2+x(2)·\sin(xdata(i))+ x(3)·xdata(i)^3
• 根据题意可知，目标函数为：\(min_x \frac{1}{2}\displaystyle{\sum_{i=1}^n}(F(x,xdata_i)-ydata_i)^2\)
• 其中：F(x,xdata) = x(1)·xdata2+x(2)\sin(xdata)+x(3)·xdata3
• 初始解向量定位 x0 = [0.3,0.4,0.1]
• 首先建立拟合函数文件 ex1024.m

      function F = ex1024(x,xdata)
      F = x(1)*xdata.^2 + x(2)*sin(xdata) + x(3)*xdata.^3;

• 再在命令行编写函数拟合代码;

      clear all
      clc
      xdata = [3.6 7.7 9.3 4.1 8.6 2.8 1.3 7.9 10.0 5.4];
      ydata = [16.5 150.6 263.1 24.7 208.5 9.9 2.7 163.9 325.0 54.3];
      x0 = [10,10,10];
      [x,resnorm] = lsqcurvefit(@ex1024,x0,xdata,ydata)

• 结果为 \(x = \begin{matrix}0.2269 &0.3385 &0.3022\end{matrix} ， resnorm = 6.2950\)，即函数在 x = 0.2269、x = 0.3385、x = 0.3022 处残差的平方和均为 6.295
• 当然了，还有一钟好用的东西叫 cftool，简直不要太简洁，入门操作请看：MATLAB如何快速进行曲线拟合