对流动人口留城意愿和多种影响因素的建立多元logistic回归模型

该全国流动人口动态监测调查的问卷中，设计有问题：“今后一段时间，您是否打算继续留在本地”（Q314），我们以此为流动人口流居其所在地意愿的依据，作为logistic回归的因变量（响应量）。

1.1 采用多元logit回归模型的原因：

该问题（Q314）的答案选项中，设计了“是”、“否”以及“没想好”三个离散的变量值，常规的二元logit回归，yi只有0和1两个取值，适用受限，因此采用多元logit回归进行分析。

1.2 自变量的选择：

1.2.1 对数据集中问题的选择和调整：

自变量包括的数值型变量：“过去一年，您家平均每月总收入”（Q105）、“出生年”（q101c1y）,转换为分类变量后代入方程中，以避免使用截面数据做回归处理中产生异方差。

将收入情况转化为“过去一年每月收入为0或亏损=1，过去一年每月收入不为0但低于4000=2，过去一年每月收入大于4000但小于10000=3”

将出年年份转化为年龄（2017当年年龄）的分类变量，具体包括“年龄在40以下=1，年龄在40到60之间，不含60=2，年龄在60及以上=3”

自变量中包含的虚拟变量选择根据问题：“性别”（q101b1）（女性=2，男性=1）、“您现在的主要职业（Q205）”、“您是否参加*医保（包括Q504A1、Q504B1、Q504C1、Q504D1）”、“你有多长时间没有回老家（户籍地）（Q310）”、“首次您是和子女一起流动吗（Q305D）”

对数据集多元分类变量的问题转化为二元变量，包括对主要的职业分为二变量（无固定职业=1，有固定职业=2）。另外对参加医保的情况转为二变量（参加一种医保=1，没有参加或不清楚=2）。对婚姻状况转化为二变量（已婚=1，未婚=2），对受教育情况转换为二变量（完成高中及以上=1，未受任何教育或未完成高中教育=2）

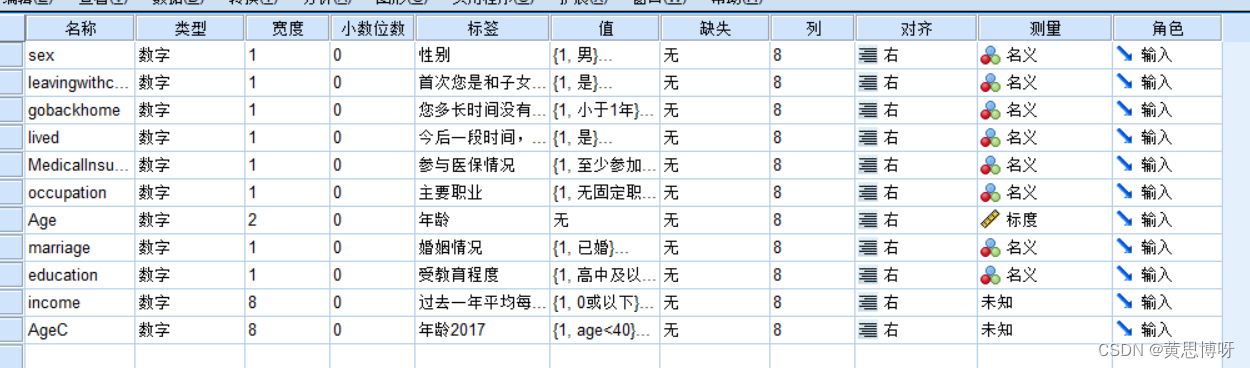
处理好的变量视图：

处理后的数据视图：

1.3 进行多元Logistic回归：

1.【分析】【回归】【多项logistic】，打开主面板—— 因变量、自变量分别按照箭头指示移入对应的变量框内：

点击【参考类别】按钮，默认勾选【最后一个类别】。（指以因变量和自变量的最后一个分类水平为参照，用其他分类依次与之对比，考察不同水平间的倾向。）

2.主面板中，点击【模型】，打开【多项logistic回归：模型】对话框，勾选【主效应】。本例主要考察自变量年龄、性别、婚姻状况的主效应，暂不考察它们之间的交互作用，然后点击【继续】。

3.主面板中，点击【统计】按钮，设置模型的统计量。主要【伪R方】【模型拟合信息】【分类表】【拟合优度】这几项必选，其他可以默认不勾选。这些参数主要用于说明建模的质量。

4.主面板中，点击【保存】按钮，勾选【估算响应概率】，我们要求SPSS软件帮我们估算每个个案三类早餐的概率。下主面板底部点击【确定】按钮，软件开始执行此处建模。

5.其余的参数主要和逐步回归有关系，本例采用主效应模型，人为指定进入模型的自变量，在其他研究中，可以根据情况选择逐步回归。

1.4 结果解读：

1、个案处理摘要：       

列出因变量和自变量的分类水平及对应的个案百分比。建议在此表主要读取变量分类水平的顺序，比如自变量参与医保的情况，第一类是“至少参与一种医保”，第二类是“无参与医保或不清楚”。尤其是看清楚最后一个分类，因为前面参数设置时要求是以最后一个分类（因变量（留城意愿）中的“没想好”）做为对比参照组的。

2、模型拟合信息和拟合优度：

读取最后一列，显著性值小于 0.05，说明模型有统计意义，模型通过检验。

原假设模型不能很好地拟合原始数据，拟合优度最后一列皮尔逊卡方显著性值小于 0.000，概率很小，拒绝原假设，说明模型对原始数据的拟合通过检验，，模型在统计学上有意义。

 

3、似然比检验： 

模型似然比检验表，我们能看到最终进入模型的效应包括截距、性别、参与医保情况、主要职业、婚姻状况、受教育程度以及没回老家的时长，而且最后一列显著性值表明，9个自变量（影响因素）对模型构成除去性别(p=0.111)以及主要职业（p=0.180），其他均有显著贡献，研究它们是有意义的。

4、多元logistic回归模型参数估计：

列出自变量不同分类水平对停留该居住地的影响检验，是多项logistic回归非常重要的结果。

第二列 B 值，即各自变量不同分类水平在模型中的系数，正负符号表明它们与因变量是正比还是反比关系。第5列是瓦尔德检验显著性值，对应的第7列显著性值小于 0.05 说明对应自变量的系数具有统计意义，对因变量不同分类水平的变化有显著影响。

对结果进行分析，查看Exp(B)值和其置信区间，即第8列，该项意义类似于OR值：

比如，有意愿留在该地和不确定是否留在该地相比，已婚的人群更偏向于选择在留在该地，这种可能性是未婚人群的 1.306 倍，95%的置信区间是(1.224,1.3993)。有参与医保相对更偏向于留在该地是没医保或不确定人群的1.235倍，95%的置信区间是(1.155,1.321)。

1.5.构建多项 logistic回归模型

G1=LOG[P(有意愿留在该地)/P(不清楚)]=1.290+0.0334(性别=1)+0.0000706(首次您是和子女一起流动的=1)+0.211(参与医保情况=1)-0.236(您多长时间没有回过老家（老家指户籍地家里）=1)-0.100(主要职业=1)+0.266(婚姻情况=1)+0.353(受教育程度=1)-0.430(过去一年平均每月收入=1)-0.245(过去一年平均每月收入=2)+0.0186(年龄2017=1)-0.077(年龄2017=2)

G2=G1=LOG[P(没有意愿留在该地)/P(不清楚)]=-1.220-0.0463(性别=1)-0.384(首次您是和子女一起流动的=1)+0.0815(参与医保情况=1)+0.0175(您多长时间没有回过老家（老家指户籍地家里）=1)-0.175(主要职业=1)-0.103(婚姻情况=1)+0.088(受教育程度=1)+0.607(过去一年平均每月收入=1)+0.080(过去一年平均每月收入=2)-0.743(年龄2017=1)-0.388(年龄2017=2)

G3=0 （对照组）

依据以上的式子，计算如下的概率值：

P1=exp(G1)/[exp(G1)+exp(G2)+exp(G3)]  #指留在本地的可能性

P2=exp(G2)/[exp(G1)+exp(G2)+exp(G3)] #指不打算留在本地的可能性

P3=exp(G3)/[exp(G1)+exp(G2)+exp(G3)] #还没想好的可能性

SPSS会自动进行模型概率预测：

对预测结果和真实结果绘制列联表，模型正确百分比=80.1%，说明模型能较好预测流动人口今后一段时间是否继续停留本地的情况。