FFT原理(基2DIT-FFT)及C语言编程思路及实现
1.FFT原理(fast Fourier transform)
首先说明:采用的是基2时域抽取法(Decimation-In-Time FFT 简称DIT-FFT)。
FFT实际上是对DFT的一种快速实现算法,实质上就是对DFT抽取,以8点DFT为例:可以分解为两个4点DFT,在继续分解为4个两点DFT,从而缩小DFT运算量,提高运算效率。(因此首先需要理解DFT算法和它的一些基本性质(周期性等))。
注意:FFT需要的采样点数要是个,若采样点数不够则需要补零处理。
具体算法推导过程如下:



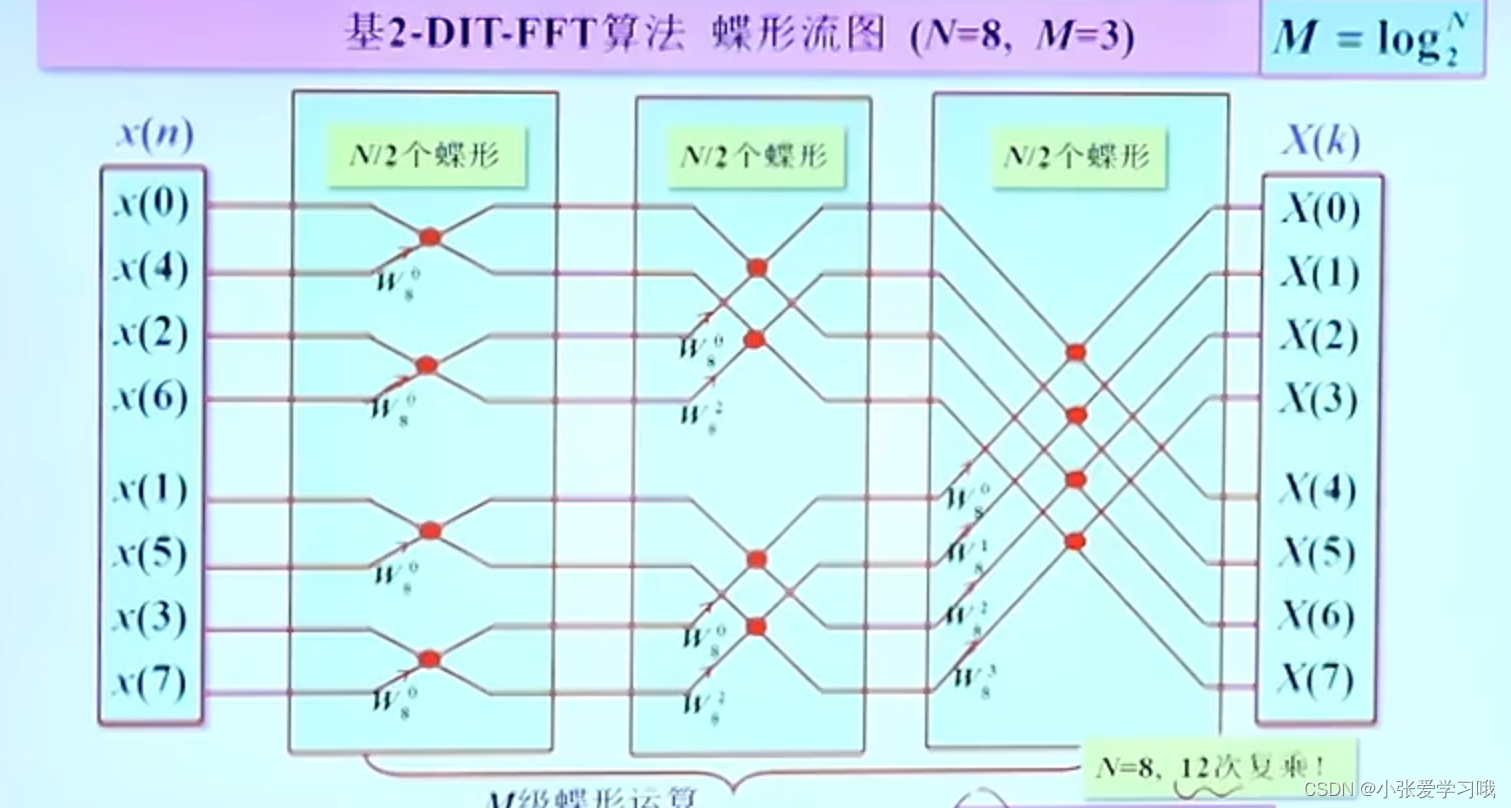
 最终得到的蝶形流图如下:
最终得到的蝶形流图如下:

2.c语言算法实现
(1)原位计算:简单理解就是每一级蝶形运算计算的结果存储到原来的存储单元就行,这样可以节省内存,降低成本。
(2)旋转因子规律
首先需要明确FFT一定是对个点进行FFT。下面以N=8为例寻找规律。根据鲽形流图,可以将
分为M级蝶形运算。具体推导如下:


下面是一个16点的蝶形流图,可以用来验证一下

(3)蝶形运算规律
已经知道旋转因子的规律了,接下来需要推导蝶形运算的规律。首先需要有一个跨度的概念(这里用B表示跨度),观察上面的8点,16点的流图,我们可以发现如下规律:
当L=1时:进行蝶形运算的两点跨度(距离)为1,这里记作B=1。
当L=2时:进行蝶形运算的两点跨度(距离)为2,这里记作B=2。
当L=3时:进行蝶形运算的两点跨度(距离)为4,这里记作B=4。
当L=4时:进行蝶形运算的两点跨度(距离)为8,这里记作B=8。
依次类推:则第L级跨度为:。
因此最终得到如下蝶形运算形式:

(5)序列的倒序
上面所进行的所有操作都是在对采样点进行重新排序之后进行的,在进行上述操作前需要对序列进行重新排序(倒序)以N=8为例输入为x(0),x(1),x(2),x(3),x(4),x(5),x(6),x(7)。需要重新排序为x(0),x(4),x(2),x(6),x(1),x(5),x(3),x(7)。这个操作就叫做倒序。首先观察下面16点的正序和倒序的二进制图如下:

i相对容易,每一行只需要加1就可以,j如果从左往右看其实本质上也是加1,因此问题难点实质上在于右边如何从8到4到12等等。这里关键是权重的概念,讲起来可能相对困难,这里大家可以结合下面的代码,调试观察,尝试几组数据之后相信一定可以理解。
框图:

#include<stdio.h>
int main()
{
int N;
printf("请输入需要倒序的个数:");
scanf("%d",&N);
int a[N];
int i=0;
//原始数据赋值
for(i=0;i<N;i++)
a[i]=i;
printf("原始数据值为");
for(i=0;i<N;i++)
printf("%-4d",a[i]);
printf("\n");
int lh=N/2,j=lh,n1=N-2;
int index,k;
//重新排序部分
for(i=1;i<n1;i++){
if(i<j){
index=a[j];
a[j]=a[i];
a[i]=index;
}
k=lh;
while(j>=k){
j=j-k;
k=k/2;
}
j=j+k;
}
printf("倒序数据值为");
for(i=0;i<N;i++)
printf("%-4d",a[i]);
return 0;
}(6)最终程序框图
到这里,需要明确对于个点,共有M级,每一级需要进行N/2此蝶形运算。第L级有
个旋转因子。可以带入到前文的流图中进性验证。具体框图入下(重点和难理解的是第三层循环,可以代入值进去理解):

(7)关于旋转旋转因子的c语言处理思路
 同时需要说明:fft进行的运算都是复数运算,因此进行的加减乘除都是复数的加减乘除。但一般在硬件上输入信号都是由ADC采集的实数信号,因此我们见到的大部分输入都是数值,但其实也可以是复数输入。
同时需要说明:fft进行的运算都是复数运算,因此进行的加减乘除都是复数的加减乘除。但一般在硬件上输入信号都是由ADC采集的实数信号,因此我们见到的大部分输入都是数值,但其实也可以是复数输入。
(8)完整程序放在这里,大家可以免费下载参考。
(9)matlab验证




3.Reference
参考华东理工大学大学万永菁老师讲的数字信号处理。想要详细学习的可以取找视频学习。
所写内容都是自己下学习fft的过程,其中可能有一些错误,如发现 还望大家指正。
更多推荐
 已为社区贡献2条内容
已为社区贡献2条内容







所有评论(0)