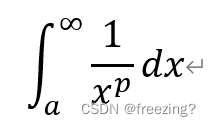
【高等数学】反常积分敛散性的判定工具——P积分的敛散性
·
反常积分的敛散性判定
反常积分又叫广义积分。广义积分判别法只要研究被积函数自身的性态,即可知其敛散性。它不仅比传统的判别法更加精细,而且避免了传统判别法需要寻找参照函数的困难。
反常积分收敛判别法规律：积分后计算出来是定值，不是无穷大，就是收敛；积分后计算出来的不是定值，是无穷大，就是发散 。
P积分的作用
一般P积分作为判断敛散性的工具，利用比较判定法的极限形式，对反常积分进行敛散性的判定。
证明
a) 当p<1时1-p>0，积分分式部分为正实数定值，而幂部分为正指数幂且根据积分上下限可得此部分趋于无穷，所以整体积分结果的极限趋于无穷，因此反常积分是发散的。
b) 当p<1时1-p<0，积分分式部分为负实数定值，而幂部分为负指数幂且根据积分上下限可得此部分为定值，所以整体积分结果的极限趋于某定值，因此反常积分是收敛的。
结论
利用好p积分的敛散性结论，可以帮助我们快速准确的判断出大多数无穷区间的反常积分的敛散性。
旨在为数千万中国开发者提供一个无缝且高效的云端环境，以支持学习、使用和贡献开源项目。
更多推荐
15
0- 0
已为社区贡献2条内容
所有评论(0)