卡尔曼滤波模型及Matlab模型建立

一、卡尔曼滤波1.概念解析：对于已知状态空间表达的线性系统，通过递归算法，基于对下一时刻状态估计误差与观测器的测量误差的数据融合，得到下一时刻状态的最优预测值。其中，引入估计误差的协方差矩阵P表征状态变量之间的相关性；引入系统误差w和观测误差v表征在预测及测量过程中会存在偏差的实际情况。由于任何外部状态通常呈现正态分布，假设,（即w服从以0为期望，Q为协方差矩阵的正态分布；v服从以0为期望，R为协

文章共5,080字 · 阅读需要大约17分钟

一键AI生成摘要，助你高效阅读

问答

锅小白

13877人浏览 · 2022-01-26 21:05:47

锅小白 · 2022-01-26 21:05:47 发布

二、扩展卡尔曼滤波（EKF:Extended KAlman Filter）

1.非线性系统的局部线性化

2.扩展卡尔曼滤波模型

一、卡尔曼滤波

卡尔曼滤波的目的：由于人的主观认识（数学模型的建立而产生的理论状态值）和测量（传感器等测量值）都不准确，引入卡尔曼滤波，综合两者的误差，得到最优的对于真实值的预测。

1.概念解析：

对于已知状态空间表达 $\left\{\begin{matrix} x_{k}=Ax_{k-1}+Bu_{k-1}+w_{k-1})(1)\\ z_{k}=Hx_{k-1}+v_{k}(2) \end{matrix}\right.$ 的线性系统，通过递归算法，基于对下一时刻状态估计误差与观测器的测量误差的数据融合，得到下一时刻状态的最优预测值。

其中，引入估计误差的协方差矩阵P表征状态变量之间的相关性；引入系统误差w和观测误差v表征在预测及测量过程中会存在偏差的实际情况。由于任何外部状态通常呈现正态分布，假设 $w\sim N(0,Q)$ , $v\sim N(0,R)$ （即w服从以0为期望，Q为协方差矩阵的正态分布；v服从以0为期望，R为协方差矩阵的正态分布）。

状态方程中， $x_{k}$ 表示第k时刻的状态量， $u_{k}$ 表示第k时刻的输入量， $z_{k}$ 表示k时刻的观测值，矩阵H为观测矩阵。

概念框图：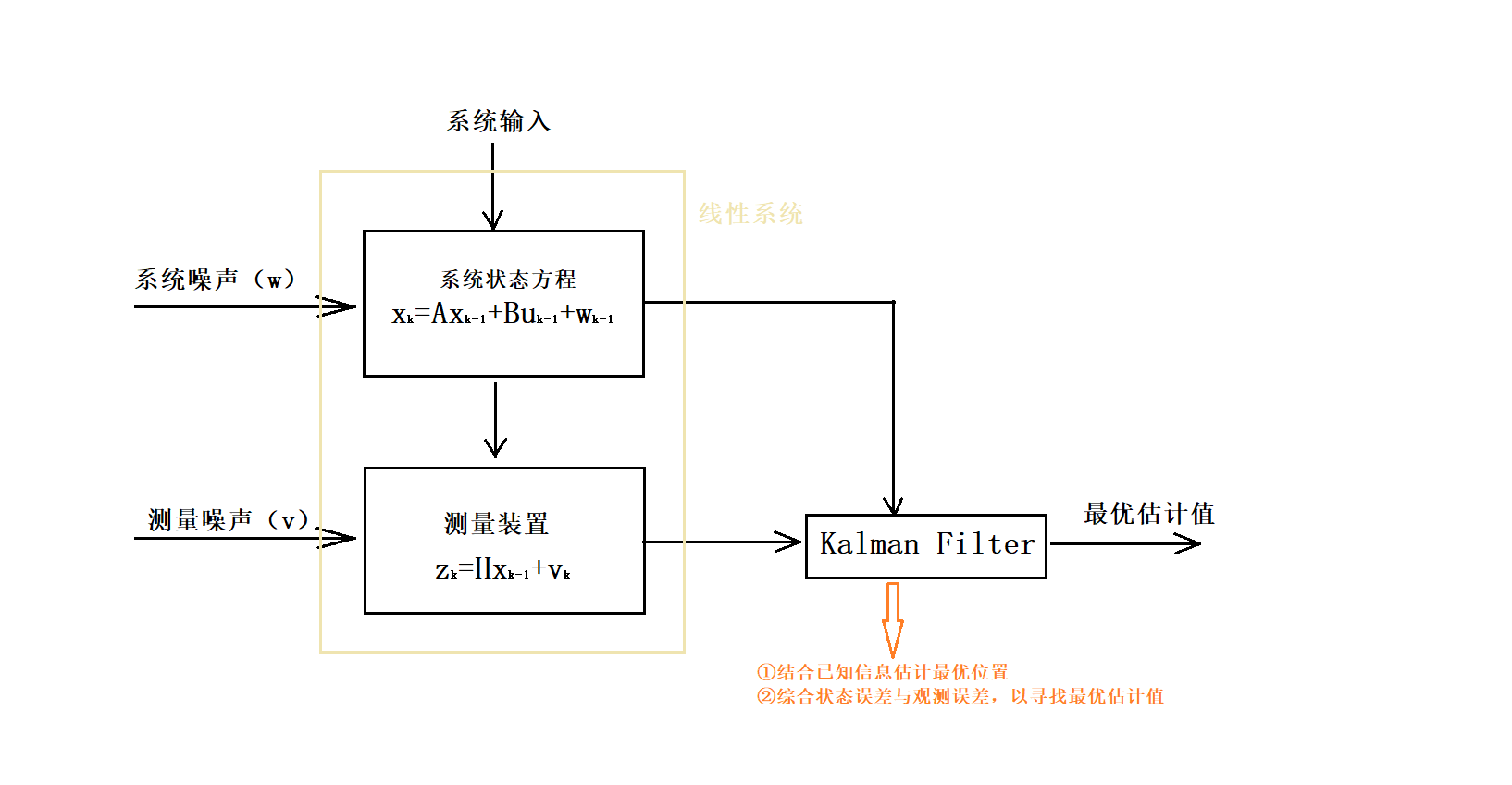

2.卡尔曼滤波的最优估计模型

1）预测：①先验 $\widehat{x_{k}^{-}}=A\widehat{x_{k-1}}+Bu_{k-1}$

②先验误差协方差 $P_{k}^{-}=AP_{k-1}A^{T}+Q$

2) 校正：①卡尔曼增益 $K_{k}=\frac{P_{k}^{-}H^{T}}{HP_{k}^{-}H^{T}+R}$

②后验估计 $\widehat{x_{k}}=\widehat{x_{k}^{-}}+K_{k}(z_{k}-H\widehat{x_{k}^{-}})$

③更新误差协方差 $P_{k}=P_{k}^{-}-K_{k}HP_{k}^{-}=(I-K_{k}H)P_{k}^{-}$

公式推导详见：（DR_CAN老师讲解的所有系列都超级推荐！！！）【卡尔曼滤波器】3_卡尔曼增益超详细数学推导～全网最完整_哔哩哔哩_bilibili

简单解释：①k时刻的先验估计为上一时刻的最优预测值；

②误差协方差矩阵P用来描述该时刻状态变量间的联系；Q为噪音矩阵，意思是变量间关系也受外界影响；

③R为观测矩阵，卡尔曼增益的大小取决于系统变量间的关系（协方差矩阵P）及观测器的性能（H、R）

④后验估计值对观测结果的依赖程度体现在 $K_{k}$ ，目的是让最优估计值的方差更小

⑤每一帧状态变量改变后，变量间的关系随之改变，故 $P_{k}$ 要时刻更新。

3.实例——小车匀加速直线运动

4.Matlab建模

假设模型参数：过程预测噪声的协方差矩阵 $Q=\begin{bmatrix} 1 &0 \\ 0&1 \end{bmatrix}$ ,

观测噪声的协方差矩阵 $R=\begin{bmatrix} 1 &0 \\ 0&1 \end{bmatrix}$ ，状态方程中 $A=\begin{bmatrix} 1 &1 \\ 0&1 \end{bmatrix}$ , $B=\begin{bmatrix} \frac{1}{2}\\ 1 \end{bmatrix}$ ,观测矩阵 $H=\begin{bmatrix} 1 &0 \\ 0&1 \end{bmatrix}$

初始状态： $X_{0}=\begin{bmatrix} 0 & 1 \end{bmatrix}$ ， $\widehat{X_{0}}=\begin{bmatrix} 0 & 1 \end{bmatrix}$ ， $P_{0}=\begin{bmatrix} 1 &0 \\ 0&1 \end{bmatrix}$ ，则代码如下：

%%先对不同变量进行定义
    %Q为过程预测噪声的协方差矩阵
    %R为观测噪声协方差矩阵
    %状态变量X=[p v],p为小车的位置，v为速度;输入u为加速度（=外力/质量）
    %X为实际状态
    %X_bar 为先验估计
    %Xbar为后验估计，最优估计值
    %P_为先验估计误差的协方差矩阵
    %P为后验估计误差的协方差矩阵
    %Z为观测量
    %K为卡尔曼增益
    
%%定义超参数
over = 50;%指定循环的遍数，即预测50s内的运动
Q = [0.1 0;0 0.1];%假设的过程预测噪声的协方差矩阵（实际上是一个变量，很难得到）
R = [1 0;0 1];%假设的观测噪声协方差矩阵（实际上也是变量，但是可以得到）

%定义尺寸参数
T = [over,2];%定义over行2列（2维状态）的矩阵，用于记录所有时刻的预测状态
delta_t = 1;%时间间隔

%假设小车为匀加速运动，加速度为1
u = 1;

%建立预测模型
A = [1 delta_t;0 1];
B = [(delta_t^2)/2;delta_t];

H =[1 0;0 1];%假设观测值的观测矩阵

I = [1 0;0 1];%定义单位矩阵

%初始化参数，由于Kk、Pk为二维矩阵，故包含所有迭代数据的K、P均为2行T列矩阵
X = zeros(T);
X_bar = zeros(T);
Xbar = zeros(T);
Z = zeros(T);
K = zeros([2*over,2]);
P = zeros([2*over,2]);
P_ = zeros([2*over,2]);

%在t=0时刻的初始值
P(1:2,:)=[1 0; 0 1];%初始前两行协方差矩阵为[1 0;0 1]，表示状态变量间相互独立
X(1,:) = [0 1];%实际状态初始值，即假设初始位置为0，初始速度为1
Xbar(1,:) = [0 1];%状态预测量的初始值;my error:①Xbar(1)表示矩阵的第一个元素②Xbar(1,:)可以表示第一行，注意是冒号:

%%卡尔曼滤波的核心算法
for n = 2:over
    %计算X的实际值：X(k)=AX(k-1)+W
    w1 = normrnd(0,sqrt(Q(1)),[1,1]);%w1是以0为均值，Q矩阵第一个元素的开方为标准差的服从正态分布的随机数
    w2 = normrnd(0,sqrt(Q(4)),[1,1]);%w2是以0为均值，Q矩阵右下方元素的开方为标准差的服从正态分布的随机数
    W = [w1 w2];%过程估计误差矩阵
    Tmp1 = A*X(n-1,:)'+B*u+W';
    X(n,:) = Tmp1';%在t=n时刻的状态实际值X(n)
    
    %计算状态的观测值：Z(k)=HX(k)+V
    v1 = normrnd(0,sqrt(R(1)),[1,1]);%v1是以0为均值，R矩阵左上角元素的开方为标准差的服从正态分布的随机数
    v2 = normrnd(0,sqrt(R(4)),[1,1]);%v2是以0为均值，R矩阵右下方元素的开方为标准差的服从正态分布的随机数
    V = [v1 v2];%观测误差矩阵
    Tmp2 = H*X(n,:)'+V';
    Z(n,:) = Tmp2';%在t=n时刻的状态观测值Z(n)
    
    %先验预测：X_bar(k)=AXbar(k-1)+Bu(k-1)
    Tmp3 = A*Xbar(n-1,:)'+B*u;%更新先验估计，k时刻的先验模型为上一时刻（k-1）的状态最优模型;注意计算时用X与u的转置，因为状态方程中状态x与输入u是列向量
    X_bar(n,:) = Tmp3';
    
    P_(((2*n-1):(2*n)),:) = A*P(((2*n-3):(2*n-2)),:) *A'+Q;%更新先验估计误差协方差:P_bar(k)=A*Pbar(k)*A'+Q
    
    %后验校正
    %卡尔曼增益
    K(((2*n-1):(2*n)),:) = P_(((2*n-1):(2*n)),:)*H'/(H*(P_(((2*n-1):(2*n)),:)*H' + R));
    %后验估计预测值：Xbar(k)=X_bar(k)+K(Z(k)-H*X_bar(k))
    Tmp4 = X_bar(n,:)' + K(((2*n-1):(2*n)),:)*(Z(n,:)'-H*X_bar(n,:)');
    Xbar(n,:) = Tmp4';
    
    P(((2*n-1):(2*n)),:) = (I-K(((2*n-1):(2*n)),:)*H)*P_(((2*n-1):(2*n)),:);%协方差矩阵P(k)更新：P(k)=(I-KH)*P_bar(k)
end

%%绘图
figure
LineWidth = 2;
%分裂窗口为2*1个子窗口
%位置曲线图
subplot(2,1,1)
plot(Z(:,1),'k-')%画出测量值
hold on;

plot(Xbar(:,1),'b-')%画出最优估计值
hold on;

plot(X(:,1),'y-')%画出实际状态值
hold on;
title('位置状态曲线')

legend('位置测量值','位置最优估计值','实际位置')%同一图像中包含多条曲线时，依次加标注
%速度曲线图
subplot(2,1,2)
plot(Z(:,2),'k-')%画出测量值
hold on;

plot(Xbar(:,2),'b-')%画出最优估计值
hold on;

plot(X(:,2),'y-')%画出实际状态值
hold on;
title('速度状态曲线')

legend('速度测量值','速度最优估计值','实际速度')

运行的状态曲线为：

注：Q,R的数值不断调整，得到的估计效果不同

参数寻优：使最优估计值更好地拟合实际值。

二、扩展卡尔曼滤波（EKF:Extended KAlman Filter）

对于非线性系统，其状态空间不能表示为 $x_{k}=Ax_{k-1}+Bu_{k-1}$ 的形式，则上述卡尔曼滤波模型不成立，并且正态分布的随机变量经过非线性系统的处理后，不再满足正态分布（Q,R也应作相应改变）。

1.非线性系统的局部线性化

在操作点附近进行局部线性化（泰勒展开)，得到非线性系统的最优预测模型——扩展卡尔曼滤波模型：

对于系统 $\left\{\begin{matrix} x_{k}=f(x_{k-1},u_{k-1},w_{k-1})\\ z_{k}=h(x_{k},v_{k}) \end{matrix}\right.$ ,f、h均为非线性函数：

由于系统存在估计和观测等误差，无法在真实点进行线性化，模型中选取f在（k-1）时刻的后验估计点 $\widehat{x_{k-1}}$ 处进行线性化：

$f(x_{k})=f(\widehat{x_{k-1}},u_{k-1},w_{k-1})+A_{k-1}(x_{k}-\widehat{x_{k-1}})+W_{k-1}w_{k-1}$

$z_{k}=h(\widetilde{x_{k}},v_{k})+H_{k}(x_{k}-\widetilde{x_{k}})+V_{k}v_{k}$

其中， $\widetilde{x_{k}}$ 为估计误差为0时的预测点，即 $\widetilde{x_{k}}=f(\widehat{x_{k-1}},u_{k-1},0)$ ；矩阵 $A_{k},W_{k},H_{k},V_{k}$ 均为雅克比矩阵做系数矩阵，且随k变化而时刻更新。

$A_{k-1}=\frac{\partial f}{\partial x}|_{(\widehat{x_{k-1}},u_{k-1})}$ , $W_{k-1}=\frac{\partial f}{\partial w}|_{(\widehat{x_{k-1}},u_{k-1})}$ , $H_{k}=\frac{\partial h}{\partial x}|_{\widetilde{x_{k}}}$ , $V_{k}=\frac{\partial h}{\partial v}|_{\widetilde{x_{k}}}$

综上，得到的线性系统为：

$\left\{\begin{matrix} x_{k}=\widetilde{x_{k}}+A_{k-1}(x_{k}-\widehat{x_{k-1}})+W_{k-1}w_{k-1}\\z_{k}=\widetilde{z_{k}}+H_{k}(x_{k}-\widetilde{x_{k}})+V_{k}v_{k} \end{matrix}\right.$