---

前言

  图像的旋转是指以图像中的某一点为原点以逆时针或者顺时针方向旋转一定的角度。通常是绕图像的起始点以逆时针进行旋转。

---

一、图像旋转算法

1.算法原理

  图像旋转计算公式如下：$$i^{\prime }=i\cos \theta -j\sin \theta$$$$j^{\prime }=i\sin \theta +j\cos \theta$$
其中，$(i,j)$是原图像$f(i,j)$中的像素点坐标；$(i^{\prime },j^{\prime })$是对应像素点$(i,j)$经过旋转变换后的图像$g(i^{\prime },j^{\prime })$的坐标。

上面的这个公式是图像绕某一点O逆时针旋转$\theta$度后的坐标。下面从数学角度推理下这个公式是如何来的。

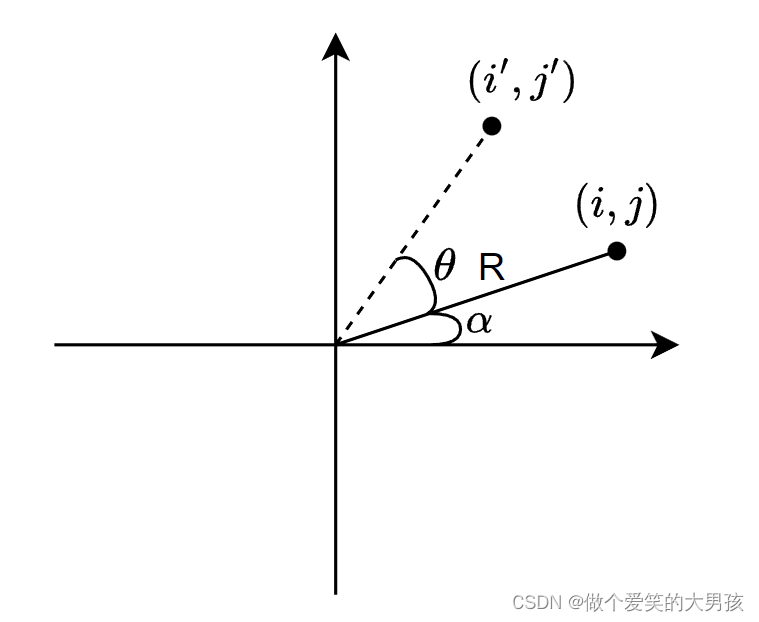
原坐标点距离旋转中心的长度为$R$，与$x$轴的夹角记为$\alpha$，逆时针旋转的角度为$\theta$，旋转后得到的新的坐标点为$(i^{\prime },j^{\prime })$。
则可知
$$\begin{gathered} i=R\cos \alpha \\ j=R\sin \alpha \end{gathered}$$
记为式(一)。
同时
$$\begin{gathered} i^{\prime }=R\cos (\alpha +\theta ) \\ {j}^{\prime }=R\sin (\alpha +\theta ) \end{gathered}$$
记为式(二)。
由三角公式可得：
$$\begin{gathered} \cos (\alpha +\theta )=\cos \alpha \cos \theta -\sin \alpha \sin \theta \\ \sin (\alpha +\theta )=\sin \alpha \cos \theta +\cos \alpha \sin \theta \end{gathered}$$
记为式(三)。将式(一)与式(三)同时带入式(二)便可得到：
$$\begin{gathered} i^{\prime }=i\cos \theta -j\sin \theta \\ {j}^{\prime }=i\sin \theta +j\cos \theta \end{gathered}$$
如上便是逆时针旋转时的数学推理过程。

顺时针旋转时这里不给出推导过程（和逆时针类似），只给出结论，如下：
$$\begin{gathered} i^{\prime }=i\cos \theta +j\sin \theta \\ {j}^{\prime }=j\cos \theta -i\sin \theta \end{gathered}$$

2. 一些需要注意的点

1. 旋转只改变图像中像素的位置，不改变像素的值；
2. 因为图像的坐标值只能是正整数，所以根据上式计算出的新的坐标位置还需要进行处理；
3. 因为旋转后的图像中间会出现空白点，所以要插值法对空白点进行插值。常用的插值方法有邻近插值法，均值插值法；
4. 因为旋转后图像的画布大小会发生变化，所以我们还要提前计算新图的画图大小。

3.举例

设原图为$$f=\left[\begin{array}{ccc}{f}_{11}& f_{12}& f_{13}\\ f_{21}& f_{22}& f_{23}\\ f_{31}& f_{32}& f_{33}\end{array}\right]$$
则$i$构成的矩阵为：$$i=\left[\begin{array}{ccc}1& 1& 1\\ 2& 2& 2\\ 3& 3& 3\end{array}\right]$$
$j$构成的矩阵为：$$j=\left[\begin{array}{ccc}1& 2& 3\\ 1& 2& 3\\ 1& 2& 3\end{array}\right]$$
假设此时要逆时针旋转30度，则根据上面的公式计算$i^{\prime }$和$j^{\prime }$。
$$i^{\prime }=i\cos 30°-j\sin 30°$$$$j^{\prime }=i\sin 30°+j\cos 30°$$
如果要顺时针旋转30度，加个负号就可以了。
计算出的$i^{\prime }$构成的矩阵为：
$$i^{\prime }=\left[\begin{array}{ccc}0.4& -0.1& -0.6\\ 1.2& 0.7& 0.2\\ 2.1& 1.6& 1.1\end{array}\right]$$
此时我们可以看到$i^{\prime }$中出现了负数和小数，这在我们编程中是行不通的，所以我们将$i^{\prime }$这个矩阵先进行四舍五入。
$$i^{\prime }=i^{\prime }-\min (i^{\prime })=i^{\prime }-(-0.6)=\left[\begin{array}{ccc}0& 0& -1\\ 1& 1& 0\\ 2& 2& 1\end{array}\right]$$
又因为坐标没有负数，所以我们将$i^{\prime }$中的每个元素加上2变成正整数得
$$i^{\prime }=\left[\begin{array}{ccc}2& 2& 1\\ 3& 3& 2\\ 4& 4& 3\end{array}\right]$$
同理可得$$j^{\prime }=\left[\begin{array}{ccc}1& 2& 3\\ 2& 3& 4\\ 2& 3& 4\end{array}\right]$$

现在我们可以找到对应关系了，例如：原图中的(1,1)点对应新图中的(2,1)点。旋转处理后的的图像数据为：
$$g=\left[\begin{array}{cccc}0& 0& f_{13}& 0\\ f_{11}& f_{12}& 0& f_{23}\\ 0& f_{21}& f_{22}& f_{33}\\ 0& f_{31}& f_{32}& 0\end{array}\right]$$
从得到的$g$矩阵中我们可以看到，$g_{23}$是一个空穴点，这一点我们需要利用插值法进行填补。其他为0的点则是属于画布上的空白点。

4. 均值插值法

  均值插值法是将空穴像素周围像素值的均值作为填充值填在该空穴点中，如下图所示：

背景为浅蓝色的点为空穴点，像素值为0。那为什么其他像素值为0的点不是空穴点呢？这里我们给出一个定义：如果一个像素值为0的点的上、下、左、右四个位置处的像素值都不为0，那我们就认为该点是空穴点，需要进行填充。
填充方式就是：$$g_{23}=(f_{13}+f_{12}+f_{23}+f_{22})/4$$

二、编程实现

1.C++代码

int main()
{
    cv::Mat img = cv::imread("Lena.bmp");

    cv::Mat gray_img(img.cols,img.rows, CV_8UC1);
    cv::cvtColor(img, gray_img, CV_BGR2GRAY);
    float theta =45;
    float curvature = theta / 180 * CV_PI;

    cv::Mat x = cv::Mat::zeros(img.size(), CV_32FC1);
    cv::Mat y = cv::Mat::zeros(img.size(), CV_32FC1);

    for (int row = 0; row < img.rows; row++)
    {
        for (int col = 0; col < img.cols; col++)
        {
            // 计算新的坐标
            x.at<float>(row, col) = round(row * cos(curvature) - col * sin(curvature));
            y.at<float>(row, col) = round(row * sin(curvature) + col * cos(curvature));
        }
    }
    double x_min, x_max;
    double y_min, y_max;
    
    cv::minMaxLoc(x, &x_min, &x_max);
    cv::minMaxLoc(y, &y_min, &y_max);
    x = x - x_min; 
    y = y - y_min;

    cv::minMaxLoc(x, &x_min, &x_max); // 画布的高
    cv::minMaxLoc(y, &y_min, &y_max); // 画布的宽

    cv::Mat dst = cv::Mat::zeros(x_max+1, y_max+1, CV_8UC1);  //幕布
    cv::Mat flag = cv::Mat::zeros(x_max + 1, y_max + 1, CV_8UC1);

    for (int row = 0; row < gray_img.rows; row++)
    {
        for (int col = 0; col < gray_img.cols; col++)
        {
            int i = (int)x.at<float>(row, col);
            int j = (int)y.at<float>(row, col);
            dst.at<uchar>(i, j) = gray_img.at<uchar>(row, col);
            flag.at<uchar>(i, j) = 1;
        }
    }
    //均值插值法对空穴进行插值
    for (int row = 1; row < dst.rows-1; row++)
    {
        for (int col = 1; col < dst.cols-1; col++)
        {
            if (flag.at<uchar>(row, col - 1) == 1 && flag.at<uchar>(row, col + 1) == 1 &&
                flag.at<uchar>(row - 1, col) == 1 && flag.at<uchar>(row + 1, col) == 1
                && flag.at<uchar>(row, col) == 0)
            {
                dst.at<uchar>(row, col) = uchar((dst.at<uchar>(row, col - 1) + dst.at<uchar>(row, col + 1) +
                    dst.at<uchar>(row - 1, col) + dst.at<uchar>(row + 1, col)) / 4);
            }
        }
    }
    cv::imshow("input", gray_img);
    cv::imshow("output", dst);
    cv::waitKey(0);
    return 0;
}

2.实验结果

---

参考资料

1.数字图像处理基础.朱虹.