ARMA模型性质之平稳AR模型得统计性质
1.均值Green函数定义Green函数递推公式2.方差举例:方法1:方法2:3.协方差函数举例1:举例2:4.自相关系数常用的ARA模型自相关系数递推公式:AR模型自相关系数的性质举例总结:
目录
1.均值
如果AR(p)模型满足平稳性条件,则
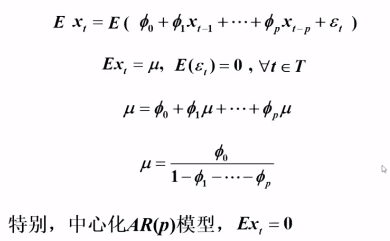
Green函数定义
AR模型得传递形式:
![]()
因为均值的性质,则有:
![]()
则,求得Xt 为
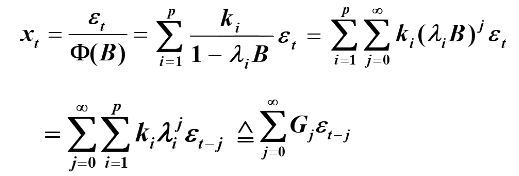
则有Green函数:
![]()
记
则模型可简记为
Green函数递推公式
因为:
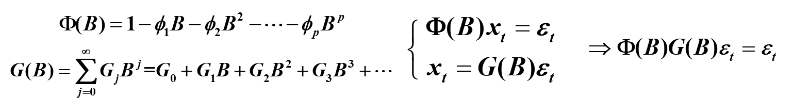
则有:
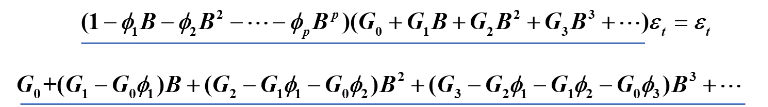
再可解得:
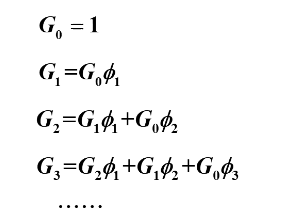
则有得出规律公式为:
![]()
则有总结如下:

2.方差
平稳AR模型得传递形式

两边求方差得
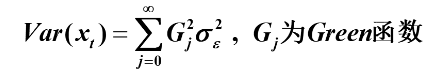
举例:
![]()
方法1:
根据Green函数:
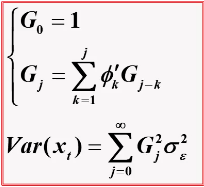
可求得如下:
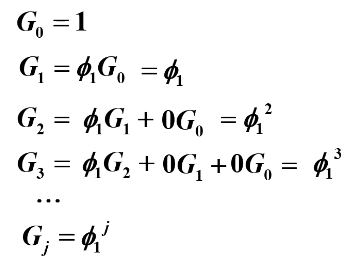
最后得出平稳AR(1)模型的方差
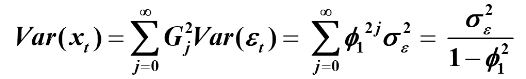
方法2:
平稳AR(1) 模型
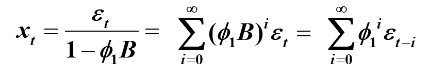
两边求方差

AR(2)模型的方差为:
利用Green 函数可以推导出 AR(2) 模型的方差为:
3.协方差函数
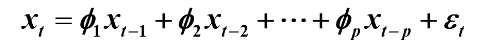
两边求期望得:
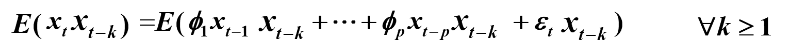
又因为
可得到协方差函数得递推公式
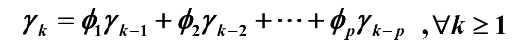
举例1:
![]()
AR(1)模型为:
![]()
递推公式:
![]()
因为 平稳AR(1)模型 具有如下:
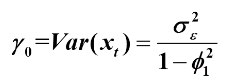
则可得该协方差函数递推公式为:
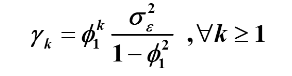
举例2:
![]()
协方差函数递推公式
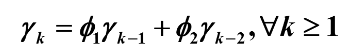
令 k = 1 可得:
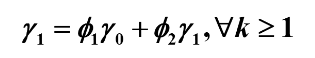
于是可得如下结论:
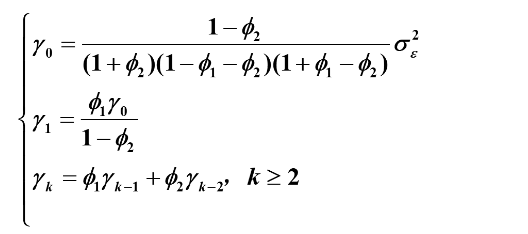
4.自相关系数
![]()
通过上式,可得到下式:

则自相关系数得定义为
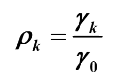
则有平稳AR(P)模型的自相关系数递推公式
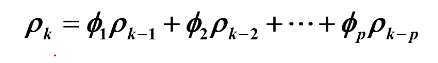
常用的ARA模型自相关系数递推公式:

其中 AR(1)模型为
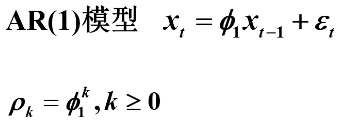
AR(2)模型为
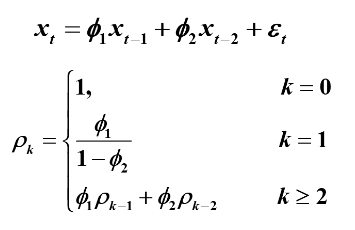
AR模型自相关系数的性质
模型:

得齐次差分方程:
![]()
设通解形式为
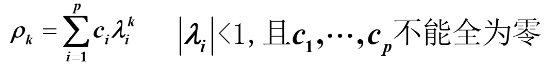
呈指数衰减

性质:拖尾性*:

举例
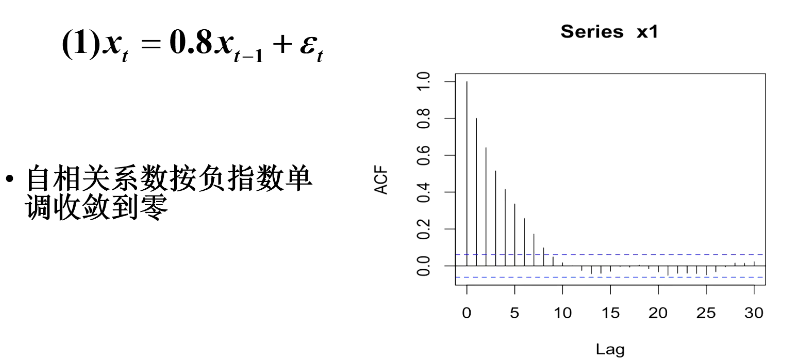
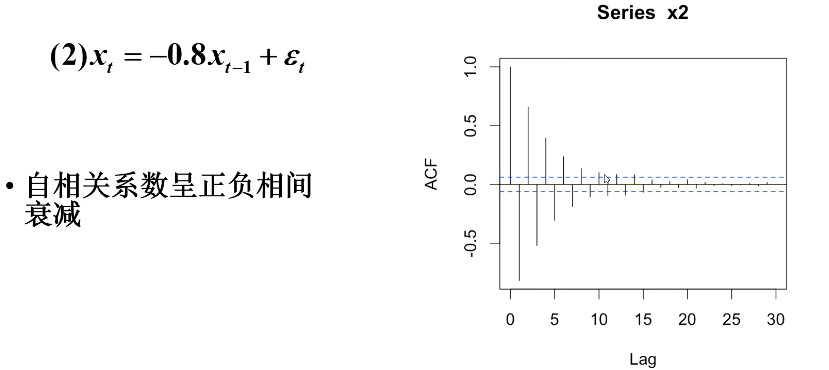
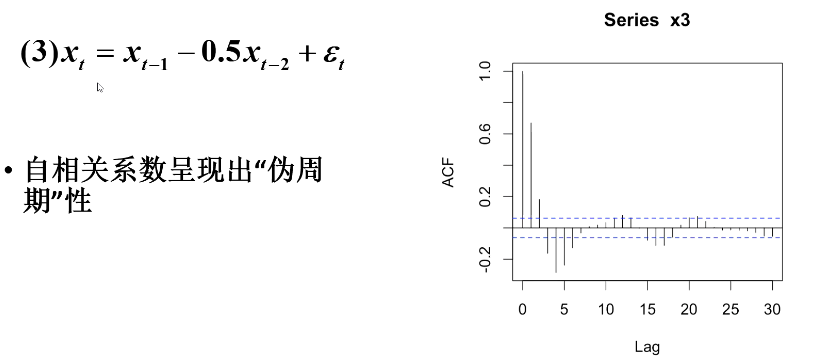
5.偏自相关系数
定义:
对于平稳AR(p)序列,所谓滞后k偏自相关系数就是指在给定中间 k-1 个随机变量
的条件下,或者说,在剔除了中间 k-1 个随机变量的干扰之后,
对
影响的相关度量。用数学语言描述就是
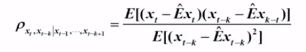
其中:
![]()
偏相关系数的计算:
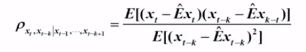
用过去的k期序列值对作k阶自回归拟合:此为式1
![]()
取条件期望:此为式2
![]()
1式 - 2式 :
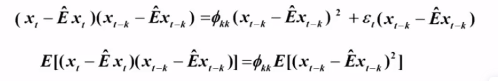
Yule - Walker 方程组:
![]()
两边同时乘 ,取期望 :
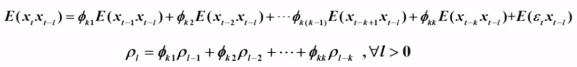
取前 k 个构成 Yule - Walker 方程组 :
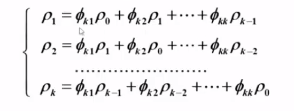
解方程组可得可得延迟k偏自相关系数
Yule - Walker 方程求解:
Yule - Walker 方程写成矩阵形式为:

根据 Cramer 法则:
![]()
其中

AR模型偏相关系数的截尾性
AR模型:
![]()
自相关系数:
![]()
Yule - Walker 方程成立:
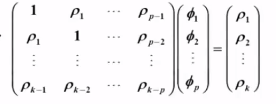
当 p>k 时:
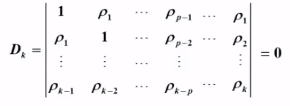
则有:
![]()
再讲一下AR模型的具体偏相关系数的解:
AR(1)模型:
![]()
Yule - Walker 方程:
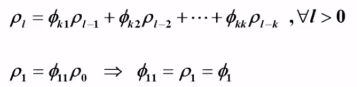
偏自相关系数的解:
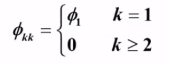
AR(2)模型:
![]()
Yule - Walker 方程:
![]()
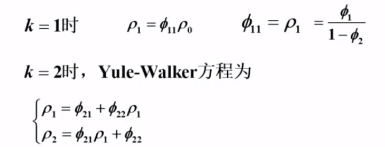
对 AR(2) 模型又有:

从而得到偏自相关系数的解:
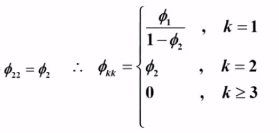
举例:
例1:
![]()
根据 AR(1) 模型的偏相关系数的解:
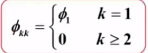
可得该问题的偏相关系数为:
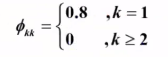
例2:
![]()
根据 AR(2) 模型的偏相关系数的解:

可得该问题的偏相关系数为:
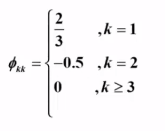
总结:
平稳AR模型得统计性质:
![]()
1.均值

2.方差
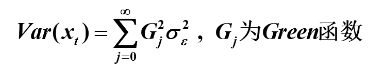
3.协方差函数
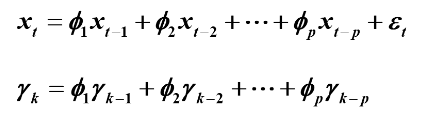
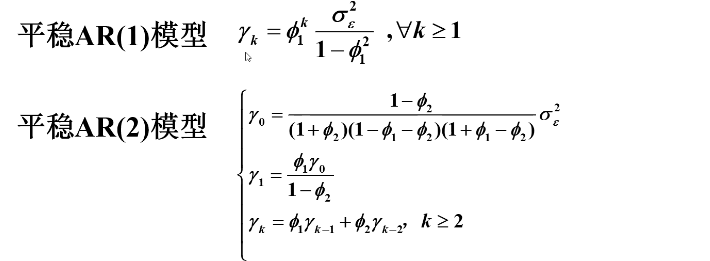
4.自相关系数
![]()
常用得AR模型自相关系数递推公式
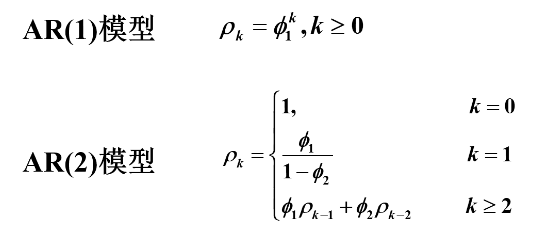
AR模型自相关系数的性质: 拖尾性
更多推荐
 已为社区贡献15条内容
已为社区贡献15条内容










所有评论(0)