欧拉角，轴角，四元数与旋转矩阵详解
入门小菜鸟，希望像做笔记记录自己学的东西，也希望能帮助到同样入门的人，更希望大佬们帮忙纠错啦~侵权立删。
目录
一、欧拉角
1、静态定义
对于在三维空间里的一个参考系，任何坐标系的取向，都可以用三个欧拉角来表现。
🌳参考系又称为实验室参考系，是静止不动的。
🌳坐标系则固定于刚体，随着刚体的旋转而旋转。
来一个经典的示例：
设定xyz-轴为参考系的参考轴（即下图蓝色部分）。称xy-平面与XY-平面的相交为交点线，用英文字母（N）代表。zxz顺规的欧拉角可以静态地这样定义：
α 是 x-轴与交点线的夹角，
β 是z-轴与Z-轴的夹角，
γ 是交点线与X-轴的夹角。
但是对于夹角的顺序和标记，夹角的两个轴的指定，并没有任何常规规定。所以每当用到欧拉角时，我们必须明确表示出夹角的顺序，指定其参考轴
2、欧拉角的表示
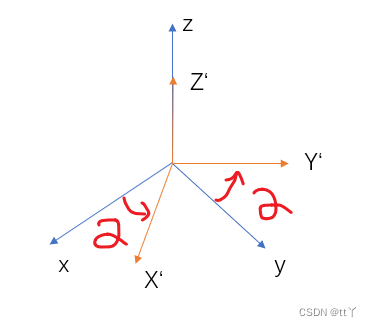
首先绕z轴转动α角（如左图），然后是绕X’轴转动β角（如中间的图），最后是绕Z’轴转动γ角（如右图），这是zxz顺规（先绕z轴，再绕x轴再绕z‘轴）的欧拉角表示方法。（除了zxz顺规外还有其他的规定方法，如xyx，zyz。这里不做详述）
欧拉角包括3个旋转，根据这3个旋转来指定一个刚体的朝向。这3个旋转分别绕x轴，y轴和z轴，分别称为 Pitch，Yaw 和 Roll。
3、欧拉角表示的优缺点
🌳优点：
（1）欧拉角由三个角度组成，直观，容易理解。
（2）可以进行从一个方向到另一个方向旋转大于180度的角度。
🌳缺点：
（1）欧拉角是不可传递的，旋转的顺序影响旋转的结果，不同的应用又可能使用不同的旋转顺序，旋转顺序无法统一；
（2）3个旋转的角度可以不受限制，即取值范围是（-inf，inf）；
（3）可能造成万向节死锁
4、欧拉角的万向节死锁（静态不存在万向锁的问题）
对于动态欧拉角（绕物体坐标系旋转），无论绕第一，三个轴转动的旋转角为多少度，只要绕第二个轴的旋转角为±90°，就会出现万向锁现象。
万向锁现象：一旦选择±90°作为pitch角，就会导致第一次旋转和第三次旋转等价，整个旋转表示系统被限制在只能绕竖直轴旋转，丢失了一个表示维度。
来个例子：
比如说我们先绕z轴转任意角度，得到下图对吧
然后咱们再绕y轴转90度，得到下图（此时Z’轴在蓝色的x-y平面上）
然后无论我们如何绕X‘轴转动，Z’轴始终在蓝色的x-y平面上，就像是被锁住了一样。
万向锁的避免问题：限制旋转的角度范围——绕第一个轴转动的旋转角限制在±180°间；绕第二个轴限制范围在±90°间。
二、四元数
1、提出意义和定义 （含轴角）
🌳提出意义：上述欧拉角是多次旋转后才能得到，那么为什么不一步到位，只旋转一次呢？那么四元数应运而生。
🌳定义：
对于一个物体的旋转，我们只需要知道四个值：一个旋转的向量 + 一个旋转的角度。而四元数也正是这样的设计：
其中x,y,z 代表的是向量的三维坐标，w代表的是角度
其实，四元数本质上是一个超复数:
🌳轴角
——这种一个轴向量（单位向量）加一个绕转角度的表示方式是轴角表示方法。
轴角最大的一个局限就是不能进行简单的插值；
此外，轴角形式的旋转不能直接施于点或矢量，必转换为矩阵或者四元数。
2、四元数的相关计算法则
（1）加法
（2）乘法
单位四元数——为了表示方便，常规定：
此时复数乘法可以表示为：
也可以表示为矩阵形式
（3）共轭 ——
3、四元数的极形式
其中 ||q|| 代表了四元数的模，单位四元数模为1，而θ是四元数表示的旋转过程的半角大小，也就是说2θ就是旋转角大小，n则是表示旋转轴方向的单位向量。
4、四元数的使用举例
一个向量：v1，要让它绕 v2 旋转θ度（顺时针转动）
那么有p = (v1, 0); q = ( v2 * sin(θ/2) , cos(θ/2) )
旋转后的四元数为（得到的四元数实部为0，虚部为新的坐标）：
5、四元数的优缺点
🌳优点：
- 存储空间小，计算效率高。
- 四元旋转不存在万向节锁问题。
🌳缺点：
- 四元数的数字表示不直观。
- 单个四元数不能表示在任何方向上超过180度的旋转。
三、四元数和欧拉角间的相互转化
1、四元数转为欧拉角
设定——
2、欧拉角转为四元数
我们设
则有：
四、旋转矩阵
假设绕XYZ三个轴旋转的角度分别为 α ，β ，γ ，则三次旋转的旋转矩阵计算方法如下：
若按Z-Y-X旋转顺序（指先绕自身轴Z，再绕自身轴Y，最后绕自身轴X），则旋转矩阵为：
欢迎大家在评论区中批评指正，谢谢~
旨在为数千万中国开发者提供一个无缝且高效的云端环境，以支持学习、使用和贡献开源项目。
更多推荐
22
0- 0
已为社区贡献22条内容
所有评论(0)