---

---

一、大地坐标系现状简析

1.1 我国

  解放后在我国大陆地区曾先后使用了三种坐标系。其一，于1954年引入了苏联1942年普尔科沃坐标系(PULK0V01942)，经局部平差建立了“1954年北京坐标系(BJ54)”，使用克拉索夫斯基(Krassowsky)椭球，原点位于前苏联普尔科沃；其二，在20世纪70年代末期，利用天文大地测量资料通过统一整体平差，建立了“1980年国家大地坐标系”，使用UGG75椭球，大地原点位于陕西省西安市北泾阳县永乐镇，又称“1980年西安大地坐标系”；其三，在1980年国家大地坐标系基础上建立“新1954年北京坐标系”，恢复使用了克拉索夫斯基椭球，有利于新坐标成果的使用和新、旧图的拼接。
  未来几年，我国将逐渐使用新一代大地坐标系“2000国家大地坐标系”（China Geodetic Coordinate System2000，CGCS2000）。其定义与协议地球参考系的定义一致，即原点是包括海洋和大气的整个地球质心，初始定向由1984.0时国际时间局定向给定，定向的时间演化使得地壳无整体旋转。

1.2 美国

  美国国防部以军事目的获取全球地面定位信息，相继建立了多个全球地心坐标系。美国国防部于1984年继WGS60、WGS66、WGS72之后建立起来第四个世界大地坐标系世界大地坐标系(World Geodetic System1984，WGS84)。WGS84规定其原点在地球质心、Z轴指向BH1984.0定义的协议地球极方向、X轴指向BH1984.0的零子午面和协议地球极赤道的交点，Y轴与X、Z轴构成右手地心地固ECEF直角坐标系。

1.3 日本

  日本在1918年之前，使用的是“日本东京1892年大地坐标系(JTD1892)”，又称“旧东京坐标系”，坐标原点在东京麻布旧东京天文台（旧海军观象台）子午仪中心点，采用1841年贝塞尔椭球，a=6377397.155米，1/f=299.1528。由于东京坐标系与WGS84坐标系的差异产生的问题日益突出。于是，2001年6月日本新测量法明确规定了其新的大地基准应该与WGS84保持一致，同时新建立的“日本大地基准2000(JGD2000)”取代了“东京坐标系”。东京坐标系通过中间坐标系Tokyo97与JGD2000大地坐标系（水平)相连，Tokyo97采用东京坐标系原点和贝塞尔参考椭球，轴向与1TRF94一致。东京坐标系坐标首先通过平差或网格内插变换至Tokyo97后，然后再变换至TRF94。这样便形成了JGD2000大地坐标系（水平），它采用GRS80椭球。

二、经纬度坐标（L,B,H）与直角坐标系坐标（X,Y,Z）相互转换

  以目前使用最为广泛的WGS84的经纬度坐标进行转换，是基于同一基准的大地坐标系转换。

2.1 正解（L,B,H）——>（X,Y,Z）

2.1.1 数学推导

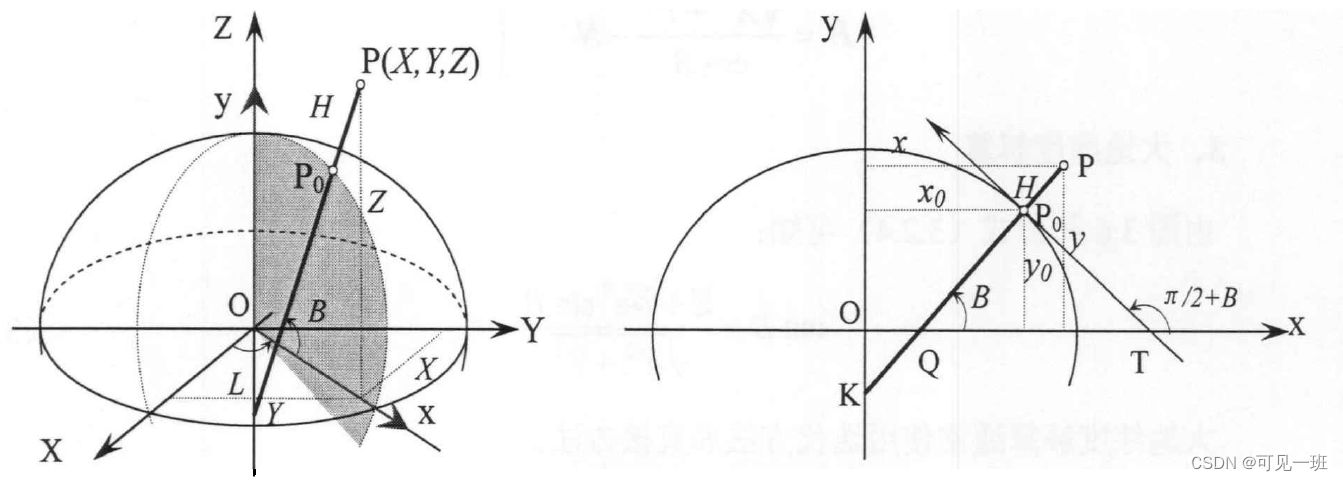
  如上示意图，求大地坐标系中点P(L,B,H)在大地空间直角坐标系的坐标(X,Y,Z)分为三步：

1. 首先，求得P点在其子午线平面坐标系O-xy内坐标(x,y)与纬度B的关系：

2. 其次，求得子午线平面坐标(x,y)在大地空间直角坐标系坐标(X,Y,Z)：
   

3. 最后，求得大地坐标系坐标P(L,B,H)在大地空间直角坐标系中的坐标(X,Y,Z)：
   

以上公式中：
a：长半轴，取 6378137m；
b：短半轴，取 6356752.3142451793m；
e^2：椭球偏心率
N：椭圆曲率半径

2.1.2 C++代码实现

原代码：lla2xyz.cpp

#include <iostream>
#include <math.h>
#include <iomanip>
constexpr double DEG_TO_RAD_LOCAL = 3.1415926535897932 / 180.0;

void LLA2XYZ(double longitude, double latitude, double height, double& X, double& Y, double& Z)
{
    double lon = longitude * DEG_TO_RAD_LOCAL;      //经度
    double lat = latitude * DEG_TO_RAD_LOCAL;
    double hei = height;

    // variable
    double a = 6378137.0;       //地球赤道半径 ，单位是 m
    double b = 6356752.31424518;    //地球短半轴 ，单位是 m
    //double E = (a * a - b * b) / (a * a);   // E = e^2
    //std::cout << "E= "<< E << std::endl;
    //double N = a/(sqrt(1-E*sin(lat)*sin(lat)));
    double N = a/(sqrt(1-((a * a - b * b) / (a * a)) * sin(lat) * sin(lat)));
    //std::cout << "N= "<< N << std::endl;

    X =(N + hei ) * cos(lat) * cos(lon);
    Y =(N + hei ) * cos(lat) * sin(lon);
    Z =((b * b * N)/ (a * a) + hei) * sin(lat) ;
}

int main()
{
    
    double longitude = 116.17;
    double latitude = 40.22;
    double height = 36.77;
    double X;
    double Y;
    double Z;

    LLA2XYZ(longitude, latitude, height, X, Y, Z);
    
    std::cout<<setiosflags(std::ios::fixed)<<"x:"<<X<<std::endl;
    std::cout<<setiosflags(std::ios::fixed)<<"y:"<<Y<<std::endl;
    std::cout<<setiosflags(std::ios::fixed)<<"z:"<<Z<<std::endl;
    return 0;
}

查看计算结果：

g++ lla2xyz.cpp -o lla2xyz
./lla2xyz

2.1.3 matlab代码实现

原代码：LLA2XYZ.m

%% WGS84经纬度LLA转直角坐标系XYZ
% 东经正数，西经为负数
% 北纬为正数，南纬为负数
% 输入参数1：纬度；输入参数2：经度；输入参数3：高度
% 经纬度单位：度；高度单位：米
% 东经116.17° 北纬40.22° 高度36.77m
function [x,y,z]=LLA2XYZ(latitude,longitude,height)
a = 6378137.0;%单位m
b = 6356752.31424518;%单位m
E = (a * a - b * b) / (a * a);

COSLAT = cos(latitude * pi / 180);
SINLAT = sin(latitude * pi / 180);
COSLONG = cos(longitude * pi / 180);
SINLONG = sin(longitude * pi / 180);
N = a / (sqrt(1 - E * SINLAT * SINLAT));
NH = N + height;
x = NH * COSLAT * COSLONG;
y = NH * COSLAT * SINLONG;
z = (b * b * N / (a * a) + height) * SINLAT;
end

查看计算结果：

[x,y,z] = LLA2XYZ(40.22 , 116.17 , 36.77 )

2.2 反解（X,Y,Z）——>（L,B,H）

2.2.1 数学推导

  对于大地空间直角坐标(X,Y,Z)计算对应的大地坐标(L,B,H)通常也分三部分：求解大地经度、求解大地纬度和计算大地高。

1. 大地经度的解算
   根据正解公式，可以得到：
   

2. 大地高的解算
   解得经度后：
   

3. 大地纬度解算
   大地纬度解算通常使用迭代方法和直接方法。
   

迭代法公式：

直接法公式：

2.2.2 C++代码实现

原代码：xyz2lla.cpp

#include <iostream>
#include <math.h>
#include <iomanip>
constexpr double DEG_TO_RAD_LOCAL = 3.1415926535897932 / 180.0;
constexpr double RAD_TO_DEG_LOCAL = 180.0 /3.1415926535897932;

void XYZ2LLA(  double X, double Y, double Z,double& longitude, double& latitude,double& altitude)
{
double a, b, c, d;
		double Longitude;// 经度
		double Latitude;// 纬度
		double Altitude;// 海拔高度
		double p, q;
		double N;
		a = 6378137.0;
		b = 6356752.31424518;
		c = sqrt(((a * a) - (b * b)) / (a * a));
		d = sqrt(((a * a) - (b * b)) / (b * b));
		p = sqrt((X * X) + (Y * Y));
		q = atan2((Z * a), (p * b));
		
		longitude = atan2(Y, X);
		N = a / sqrt(1 - ((c * c) * sin(latitude)* sin(latitude)));
		altitude = (p / cos(latitude)) - N;
		latitude = atan2((Z + (d * d) * b * pow(sin(q), 3)), (p - (c * c) * a * pow(cos(q), 3)));
		
		longitude = longitude * RAD_TO_DEG_LOCAL;
		latitude = latitude * RAD_TO_DEG_LOCAL;
}

int main()
{
    
    double longitude;
    double latitude ;
    double altitude ;
    double X=-2150931.511720;
    double Y=4377053.846931;
    double Z=4096692.121877;

    XYZ2LLA(X,Y,Z,longitude, latitude, altitude);
    
    std::cout<<setiosflags(std::ios::fixed)<<"longitude:"<<longitude<<std::endl;
    std::cout<<setiosflags(std::ios::fixed)<<"latitude:"<<latitude<<std::endl;
    std::cout<<setiosflags(std::ios::fixed)<<"altitude:"<<altitude<<std::endl;
    return 0;
}

查看计算结果：

g++ xyz2lla.cpp -o xyz2lla
./xyz2lla

2.2.3 matlab代码实现

原代码：XYZ2LLA.m

%% WGS84直角坐标系转经纬度
% 东经正数，西经为负数
% 北纬为正数，南纬为负数
% 输入参数1：纬度；输入参数2：经度；输入参数3：高度
% 经纬度单位：度；高度单位：米
function [latitude,longitude,height]=XYZ2LLA(x,y,z)
 
a = 6378137.0;
b = 6356752.31424518;
c = sqrt(((a * a) - (b * b)) / (a * a));
d = sqrt(((a * a) - (b * b)) / (b * b));
p = sqrt((x * x) + (y * y));
q = atan((z * a)/ (p * b));
longitude = atan(y/x);
latitude = atan((z + (d * d) * b * sin(q)^3)/(p - (c * c) * a * cos(q)^3));
N = a / sqrt(1 - ((c * c) * sin(latitude)^2));
height = (p / cos(latitude)) - N;
longitude = longitude * 180.0 / pi+180;
latitude = latitude * 180.0 / pi;
end

查看计算结果：

[latitude,longitude,height]=XYZ2LLA(-2150931.511720,4377053.846931,4096692.121877)