Mplus—验证性因素分析(Confirmatory Factor Analysis, CFA)
目录
参考书目
1. 《高级心理统计》 刘红云 中国人民大学出版社
2. 《潜变量建模与Mplus应用·基础篇》 王孟成 重庆大学出版社
CFA简介
验证性因素分析(Confirmatory Factor Analysis, CFA)是在探索性因素分析(Exploratory Factor Analysis,EFA)的基础上发展而来的。
CFA是对已有的理论模型与数据拟合程度的一种验证,要在对研究问题有所了解的基础上进行,这种了解可以是建立在理论、实验研究或者二者相结合的基础上。
CFA步骤
1. 模型设定
在开始验证性因素分析之前,需要根据一定的理论假设,定义观测变量(题项)与因素/潜变量之间的关系、因素/潜变量之间的关系以及误差项之间的关系。
- 存在多少个因素/维度
- 每个因素分别影响哪些观测变量
- 如果有两个及以上的因素,他们之间的关系如何
- 误差项之间的关系如何
- 观测变量的单维性,测量一个因素(潜变量)的观测变量,不能同时测量另外一个潜变量,及不能存在交叉负荷
2. 模型识别
在进行参数估计前,首先必须对所定义的模型进行识别。模型识别是指判断模型参数是否有唯一解。
决定一个模型是否可识别有几种条件。但模型识别是一个比较复杂的过程。目前我们一般根据软件输出结果来判断。
3. 模型估计(参数估计)
验证性因素分析通过比较模型导出的总体协方差矩阵与样本协方差矩阵的接近程度来反映理论模型与数据的吻合程度,通过特殊的拟合函数使二者之间的差异最小化即可获得参数的估计值。
验证性因素分析中的参数估计方法主要有:
- 未加权最小二乘法(ULS)
- 广义最小二乘法(GLS)
- 极大似然法(ML)
- 工具变量法(IV)
- 加权最小平均法(WLS)
- ……
Mplus软件中提供的方法有:
- 极大似然法(ML)
- 稳健极大似然法(MLR)
- 均值调整的极大似然法(MLM)
- 加权最小平均法(WLS)
- 均值调整的加权最小平均法(WLSM)
- ……
4. 模型评价
模型评价是指对模型与数据间是否拟合进行评价,可以通过拟合指数来评价一个模型与数据的拟合程度。
拟合指数是反映由实际数据衍生的样本的期望协方差矩阵与样本实际的协方差矩阵差异的一个总体指标。
评价一个模型时,必须综合多个拟合指数,而不能仅仅依赖其中的某一个指数。
主要的模型拟合指数及判定标准:

例如,一些文献中使用的拟合指数及判断标准
- 宽松标准:χ2/df≤5;RMSEA≤0.08;CFI≥0.90;TLI≥0.90;SRMR≤0.08
- 严格标准:χ2/df≤3;RMSEA≤0.05;CFI≥0.95;TLI≥0.95;SRMR≤0.05
5. 模型修正
如果模型不能很好地拟合数据,就需要对模型进行修正和再次设定,在这种情况下,研究者需要决定如何删除、增加和修改模型参数,通过模型修正增加模型的拟合程度。
需要进行模型修正的情况:
- 出现无统计学意义的参数或取值不恰当的参数
- 多个拟合指标显示模型拟合程度低
我们可以通过模型修正指数(Modification index)来对模型进行调整。
修正指数值表示,如果估计这条路径,模型拟合的整体卡方值会减小的数值。
但修正不能仅凭软件输出的结果进行,而应该有理论支持,具有理论上的合理性。
CFA在Mplus中的操作方法与结果解读
1. 数据:某一量表的调查数据
2. 样本量:1206人
3. 题项数量:31
4. 理论维度
- F1:1、4、7、10、13、16、19、22、25、28
- F2:2、5、8、11、14、17、20、23、26、29、31
- F3:3、6、9、12、15、18、21、24、27、30
5. 操作方法
- 整理好数据,进行数据检查,例如:最大值和最小值是否在计分范围内
- 定义缺失值
- 将SPSS数据转为.dat格式数据
- 写语法
一阶验证性因素分析语法
TITLE: CFA; ! 该语法文件的内容为验证性因素分析
DATA: FILE IS 123.dat; ! 读取的数据文件的名称为123(数据文件与语句文件放在同一文件夹内)
VARIABLE: NAME ARE x1-x31; ! 定义了数据文件中的变量,这里有31个变量,命名为x1-x31
USEVARIABLES ARE x1-x31; ! 定义了在此次分析中,所使用的变量为x1-x31,即31道题上被试得分
MISSING=ALL (99); ! 定义了缺失值,表示数据文件中的99为缺失值,不纳入分析
ANALYSIS: ESTIMATOR=MLR; !选择估计方法,稳健极大似然估计(Robust Maximum Likelihood Estimator, MLR),根据自己的数据特点,可选择其他估计方法
MODEL: F1 BY x1 x4 x7 x10 x13 x16 x19 x22 x25 x28;
F2 BY x2 x5 x8 x11 x14 x17 x20 x23 x26 x29 x31;
F3 BY x3 x6 x9 x12 x15 x18 x21 x24 x27 x30;
! BY通过观测变量定义潜变量
! 定义了模型,根据理论假设,1、4、7、10、13……28这10道题测量第一个维度/因素/潜变量,2、5、8……31这11道题测量第二个维度/因素/潜变量,3、6、9……30这10道题测量了第三个维度/因素/潜变量。程序默认三个潜变量是相关的
OUTPUT: SAMPSTAT STDYX MOD CINTERVAL; ! 结果输出:样本统计量、标准化值、模型修正指数和参数估计置信区间
二阶验证性因素分析语法
二阶/高阶模型概述
在CFA模型中,一般将与指标直接相连的因子称作一阶或者低阶因子,在一阶因子之上,对低阶因子产生影响的因子称作二阶或高阶因子。当一阶或低阶CFA模型拟合数据较好时,出于模型简化或理论考虑,有时使用一个高阶因子去解释低阶因子间的相关,即用高阶模型替代低阶模型。
二阶CFA是在一阶CFA的基础上进行的
二阶CFA要满足一阶条件:
- 一阶因子在理论上可以提炼出一个高阶的因子(一般低阶因子加总分有意义是可以进行二阶CFA的)
- 一阶因子间的相关需要中等以上
TITLE: CFA;
DATA: FILE IS 123.dat;
VARIABLE: NAME ARE x1-x31;
USEVARIABLES ARE x1-x31;
MISSING=ALL (99);
ANALYSIS: ESTIMATOR=MLR;
MODEL: F1 BY x1 x4 x7 x10 x13 x16 x19 x22 x25 x28;
F2 BY x2 x5 x8 x11 x14 x17 x20 x23 x26 x29 x31;
F3 BY x3 x6 x9 x12 x15 x18 x21 x24 x27 x30;
F BY F1 F2 F3; ! 在三个因素/维度/潜变量的基础上,提炼了一个高阶因子
OUTPUT: SAMPSTAT STDYX MOD CINTERVAL;
结果解读
1. 模型拟合

2. 非标准化结果

3. 标准化结果

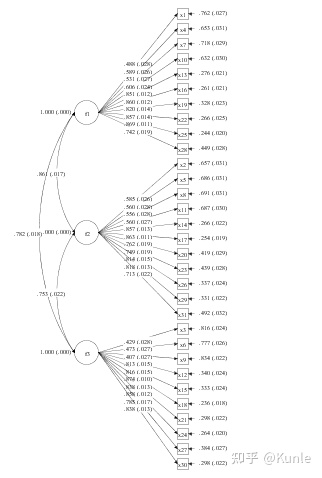
4. 一阶验证性因素分析模型图

5. 二阶验证性因素分析模型图

6. 模型修正
可根据修正指数的提示,对模型进行调整。

希望上述介绍可以帮助到你!也欢迎大家在评论区多多交流分享。
你的关注/点赞 /收藏★/分享,是最大的支持!
更多推荐
 已为社区贡献4条内容
已为社区贡献4条内容










所有评论(0)