图像分割UNet系列------UNet3+(UNet3plus)详解
图像分割unet系列------UNet3+(UNet3plus)详解
UNet3+发表于2020年的ICASSP,它是对UNet非常重要的改进,它的性能我认为是可以超过 UNet++的,至少在我的使用过程中我会直接使用UNet3+,而不是UNet++。
1、UNet3+结构
UNet3+主要是参考了UNet和UNet++两个网络结构。尽管UNet++采用了嵌套和密集跳过连接的网络结构(见图1(b)红色三角区域),但是它没有直接从多尺度信息中提取足够多的信息。此部分,在我理解而言UNet++虽然名义上通过嵌套和密集跳过连接进行了多尺度信息的利用,但是从本质上看基本都是短连接,基本上都对解码特征进行了再次处理,再加上各个连接的融合,多尺度信息的原始特征几乎没有得到特别好的利用,信号处理有些矫枉过正或是丢失。UNet3+利用了全尺度的跳跃连接(skip connection)和深度监督(deep supervisions)。全尺度的跳跃连接把来自不同尺度特征图中的高级语义与低级语义直接结合(当然需要必要的上采样操作);而深度监督则从多尺度聚合的特征图中学习层次表示。注意一点:UNet++和UNet3+都用到了深度监督,但是监督的位置是完全不一样的,从图1(b)、(c)中的Sup部分可以清楚的看到不同之处。

在UNet3+中,可以从全尺度捕获细粒度的细节和粗粒度的语义。为了进一步从全尺寸的聚合特征图中学习层次表示法,每个边的输出都与一个混合损失函数相连接,这有助于精确分割,特别是对于在医学图像体积中出现不同尺度的器官。从图1中也可以看出,UNet3+的参数量明显小于UNet++。
在介绍Res-UNet和Attention Unet两个改进算法时我们提到为了满足医学图像分割的准确性要求它们引入注意力机制(Res-UNet为hard-attention,而Attention Unet本质上是soft-attention),当然,在推理时执行预定义的细化方法(如CRF[4])也可以保障图像分割的准确性。但是,作者并没有应用这两种方法,它是利用分类任务来预测输入图像是否有器官,为分割任务提供必要的指导。
2、UNet3+主要部分说明
2.1 全尺寸跳跃连接(Full-scale Skip Connections)
全尺寸跳跃连接部分的结构如下图2所示。

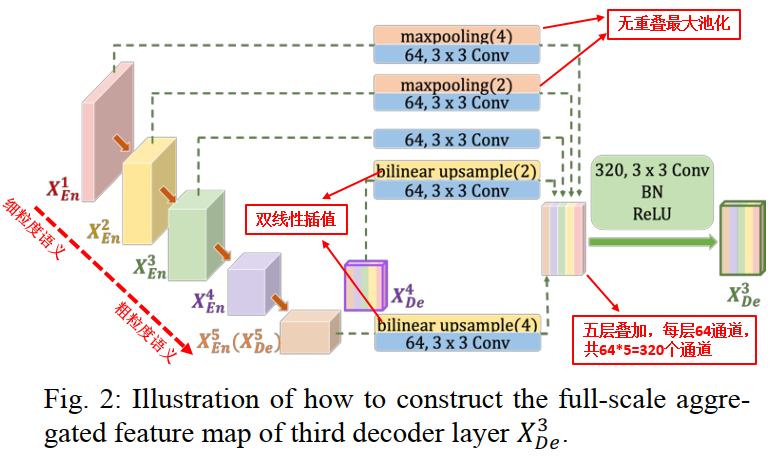
作者在文章中利用图2详细说明了构造 X D e 3 X_{D e}^{3} XDe3 特征图的全过程。从上图中可以看出,特征图 X D n 3 X_{D n}^{3} XDn3的全尺寸连接主要是来自三个部分:
- 较小尺度编码器 X E n 1 X_{E n}^{1} XEn1 和 X E n 2 X_{E n}^{2} XEn2。此部分保留了细节信息,即融合细粒度语义。 X E n 1 X_{E n}^{1} XEn1 和 X E n 2 X_{E n}^{2} XEn2要进行下采样,分别下采样4倍和2倍,以统一特征图的大小。随后进行3*3卷积,64通道。值得注意的一点:此部分的下采样采用的是无重叠最大池化。
- 相同尺度编码器的特征图 X E n 3 X_{E n}^{3} XEn3 。此层直接进行3*3卷积,64通道操作。
- 较大尺度解码器中的 X D n 4 X_{D n}^{4} XDn4 和 X E n 5 X_{E n}^{5} XEn5 。此部分融合了粗粒度语义信息。 X D n 4 X_{D n}^{4} XDn4与 X E n 5 ( X D e 5 ) X_{E n}^{5}\left(X_{D e}^{5}\right) XEn5(XDe5)分别进行2倍与4倍的上采样,也是为了保证特征图大小的统一。注意:此部分的上采样是采用双线性插值的方法。
五层叠加(拼接融合)形成320通道的特征图。随后再进行320通道的3*3卷积、BN、Relu等操作形成新的特征图 X D n 3 X_{D n}^{3} XDn3。其他解码部分的特征图生成过程类似。
2.2 UNet、UNet++和UNet3+参数数量计算与比较
在文章开始我们谈到UNet3+与UNet++和UNet相比拥有更少的参数,具体怎样通过计算进行相应的对比呢?论文中,作者进行了相关计算。首先,通过公式表示全尺寸跳跃连接,
i
i
i表示沿着编码的方向第
i
i
i个下采样层,
N
N
N表示编码器个数(论文为5个),那么特征图
X
D
e
i
X_{D e}^{i}
XDei 的计算公式如下:
X
D
e
i
=
{
X
E
n
i
,
H
(
[
C
(
D
(
X
E
n
k
)
)
k
=
1
i
−
1
,
C
(
X
E
n
i
)
⏟
Scales:
1
t
h
∼
i
t
h
,
C
(
U
(
X
D
e
k
)
)
k
=
i
+
1
N
⏟
Scales:
(
i
+
1
)
t
h
∼
N
t
h
]
)
,
i
=
1
,
⋯
,
N
−
1
(
1
)
X_{D e}^{i}=\left\{\begin{array}{l} X_{E n}^{i}, \\ \mathcal{H}\left([\underbrace{C\left(\mathcal{D}\left(X_{E n}^{k}\right)\right)_{k=1}^{i-1}, C\left(X_{E n}^{i}\right)}_{\text {Scales: } 1^{t h} \sim i^{t h}}, \underbrace{C\left(\mathcal{U}\left(X_{D e}^{k}\right)\right)_{k=i+1}^{N}}_{\text {Scales: }(i+1)^{t h} \sim N^{t h}}]\right), i=1, \cdots, N-1 \end{array}\right.(1)
XDei=⎩
⎨
⎧XEni,H
[Scales: 1th∼ith
C(D(XEnk))k=1i−1,C(XEni),Scales: (i+1)th∼Nth
C(U(XDek))k=i+1N]
,i=1,⋯,N−1(1)
其中,函数
C
(
.
)
C(.)
C(.)表示卷积操作,函数
H
(
.
)
\mathcal{H}(.)
H(.)表示特征聚合机制 (一个卷积层+一个BN+一个ReLU), 函数
D
\mathcal{D}
D和 函数
U
\mathcal{U}
U分别表示上采样和下采样操作,
[
]
[ ]
[]表示通道维度拼接融合。
从图1可以看出,UNet、UNet++和UNet3+编码器的结构三者都是一样的, X E n i X_{E n}^{i} XEni 都为 32 × 2 i 32 \times 2^{i} 32×2i 通道数,编码部分的参数都是一样多的。他们的不同主要是体现在解码部分,具体参数量的计算如下所示:
1)UNet解码部分
UNet的解码部分和编码部分是对称的, 因此
X
D
e
i
X_{D e}^{i}
XDei 都为
32
×
2
i
32 \times 2^{i}
32×2i 通道。 UNet解码部分中第
i
i
i个解码阶段的参数数量可以通过下面式子计算得到:
P
U
−
D
e
i
=
D
F
×
D
F
×
[
d
(
X
D
e
i
+
1
)
×
d
(
X
D
e
i
)
+
d
(
X
D
e
i
)
2
+
d
(
X
E
n
i
+
X
D
e
i
)
×
d
(
X
D
e
i
)
]
(
2
)
\begin{aligned} P_{U-D e}^{i}=D_{F} \times D_{F} & \times\left[d\left(X_{D e}^{i+1}\right) \times d\left(X_{D e}^{i}\right)+d\left(X_{D e}^{i}\right)^{2}\right.\\ &\left.+d\left(X_{E n}^{i}+X_{D e}^{i}\right) \times d\left(X_{D e}^{i}\right)\right] \end{aligned}(2)
PU−Dei=DF×DF×[d(XDei+1)×d(XDei)+d(XDei)2+d(XEni+XDei)×d(XDei)](2)
其中,
D
F
D_{F}
DF 表示卷积核的大小,函数
d
d
d表示求出节点的深度。
2)UNet++解码部分
在UNet++中, 它在每一条跳跃路径 上都利用了稠密卷积模块(dense conv block),它的计算公式如下:
P
U
+
+
−
D
e
i
=
D
F
×
D
F
×
[
d
(
X
D
e
i
+
1
)
×
d
(
X
D
e
i
)
+
d
(
X
D
e
i
)
2
+
d
(
X
E
n
i
+
∑
k
=
1
N
−
1
−
i
X
M
e
i
,
k
+
X
D
e
i
)
×
d
(
X
D
e
i
)
]
(
3
)
\begin{aligned} P_{U^{++}-D e}^{i}=D_{F} \times D_{F} \times[& d\left(X_{D e}^{i+1}\right) \times d\left(X_{D e}^{i}\right)+d\left(X_{D e}^{i}\right)^{2}+\\ &\left.d\left(X_{E n}^{i}+\sum_{k=1}^{N-1-i} X_{M e}^{i, k}+X_{D e}^{i}\right) \times d\left(X_{D e}^{i}\right)\right] \end{aligned}(3)
PU++−Dei=DF×DF×[d(XDei+1)×d(XDei)+d(XDei)2+d(XEni+k=1∑N−1−iXMei,k+XDei)×d(XDei)](3)
从公式看,UNet++的参数量比UNet还要大一些。
3)UNet3+解码部分
在UNet3+中, 每一个解码器由
N
N
N个尺度连接所成, 所以产生
64
×
N
64 \times N
64×N 通道,计算公式如下:
P
u
3
+
−
D
e
i
=
D
F
×
D
F
×
[
(
∑
k
=
1
i
d
(
X
E
n
k
)
+
∑
k
=
i
+
1
N
d
(
X
D
e
k
)
)
×
64
+
d
(
X
D
e
i
)
2
]
(
4
)
P_{u^{3+}-D e}^{i}=D_{F} \times D_{F} \times\left[\left(\sum_{k=1}^{i} d\left(X_{E_{n}}^{k}\right)+\sum_{k=i+1}^{N} d\left(X_{D e}^{k}\right)\right) \times 64+d\left(X_{D e}^{i}\right)^{2}\right](4)
Pu3+−Dei=DF×DF×[(k=1∑id(XEnk)+k=i+1∑Nd(XDek))×64+d(XDei)2](4)
通过公式(2)(3)(4)可以看出,虽然从网络结构上看,UNet最为清晰明了,貌似参数应该更少,其实并不是这样。在保障相同的编码部分的前提下,它们三者中UNet3+的参数量最少,其次才是UNet,UNet++的参数量是最多的(结构也最复杂)。
2.3 全尺寸深监督(Full-scale Deep Supervision)
UNet3+全尺寸深监督部分的结构如下图1所示。当然,UNet3+的深监督应该是从UNet++中得到了启发。但是,两者有很大的不同。
UNet++深监督部分
UNet++是对第一层的特征图进行深监督,即对全分辨率特征图进行深监督,见图1, X M e 1 , 1 X_{M e}^{1,1} XMe1,1 、 X M e 1 , 2 X_{M e}^{1,2} XMe1,2、 X M e 1 , 3 X_{M e}^{1,3} XMe1,3、 X D e 1 , 4 X_{D e}^{1,4} XDe1,4。在实际操作中UNet++使用1*1卷积分别对 X M e 1 , 1 X_{M e}^{1,1} XMe1,1 、 X M e 1 , 2 X_{M e}^{1,2} XMe1,2、 X M e 1 , 3 X_{M e}^{1,3} XMe1,3、 X D e 1 , 4 X_{D e}^{1,4} XDe1,4进行操作,去监督每个分支的输出。
UNet3+深监督部分
UNet3+全尺寸深监督是每个解码器对应一个侧输出(side output),通过ground truth进行监督。为了实现深度监控,每个解码器的最后一层被送入一个普通的3 × 3卷积层,然后是一个双线性上采样和一个sigmoid函数。
此处进行双线性上采样的目的我认为主要有两个:
- 上采样是将第2、3、4、5层扩展成全分辨率特征图,保证与第一层相同,这也是全尺寸深监督的关键操作;
- 双线性上采样的方式可以最大限度保证上采样过程中边缘信息的完整性(医学图像边缘的不确定性决定要尽量保障边缘信息不丢失);
UNet3+的Loss函数
为了进一步增强器官的边界,作者提出了一个基于多尺度结构相似度指数(MS-SSIM)的损失函数来赋予模糊边界更高的权重。受益于此,UNet 3+将关注模糊边界,区域分布差异越大,MS-SSIM值越高。从分割结果
P
P
P和 ground truth mask
G
G
G裁剪了两个相应的
N
×
N
N×N
N×N大小的块,它们可以分别表示为
=
{
p
j
:
j
=
1
,
…
,
N
2
}
=
1
,
…
,
N
2
}
\left.=\left\{p_{j}: j=1, \ldots, N^{2}\right\}=1, \ldots, N^{2}\right\}
={pj:j=1,…,N2}=1,…,N2} 和
g
=
{
g
j
:
j
=
1
,
…
,
N
2
}
g=\left\{g_{j}: j=1, \ldots, N^{2}\right\}
g={gj:j=1,…,N2} 。定义
p
p
p和
g
g
g 的MS-SSIM损失函数为:
ℓ
m
s
−
s
s
i
m
=
1
−
∏
m
=
1
M
(
2
μ
p
μ
g
+
C
1
μ
p
2
+
μ
g
2
+
C
1
)
β
m
(
2
σ
p
g
+
C
2
σ
p
2
+
σ
g
2
+
C
2
)
γ
m
\ell_{m s-s s i m}=1-\prod_{m=1}^{M}\left(\frac{2 \mu_{p} \mu_{g}+C_{1}}{\mu_{p}^{2}+\mu_{g}^{2}+C_{1}}\right)^{\beta_{m}}\left(\frac{2 \sigma_{p g}+C_{2}}{\sigma_{p}^{2}+\sigma_{g}^{2}+C_{2}}\right)^{\gamma_{m}}
ℓms−ssim=1−m=1∏M(μp2+μg2+C12μpμg+C1)βm(σp2+σg2+C22σpg+C2)γm
其中,
M
M
M表示尺度的总数量,
μ
p
,
μ
g
\mu_{p}, \mu_{g}
μp,μg 和
σ
p
,
σ
g
\sigma_{p}, \sigma_{g}
σp,σg 分别是
p
p
p、
g
g
g的均值和方差,
σ
p
g
\sigma_{p g}
σpg 表示它们的协方差。
β
m
,
γ
m
\beta_{m}, \gamma_{m}
βm,γm 定义每个尺度中这两个部分的相对重要性,设置可以参考[9]。加入两个小的常量
C
1
=
0.0
1
2
C_{1}=0.01^{2}
C1=0.012 和
C
2
=
0.0
3
2
C_{2}=0.03^{2}
C2=0.032 是避免除零的不稳定情况。作者将尺度设置为5(和UNet、UNet++保持一致)。
结合focal损失函数
ℓ
f
l
\ell_{f l}
ℓfl[10], MS-SSIM损失函数
ℓ
m
s
−
s
s
i
m
\ell_{m s-s s i m}
ℓms−ssim和IoU损失函数
ℓ
i
o
u
\ell_{i o u}
ℓiou[11],我们提出一种混合损失函数用于像素级别分割、块分割、图像级别分割三个不同层次的分割,它可以同时获取大尺度和精细结构中清晰的边缘。混合分割损失被定义为:
ℓ
s
e
g
=
ℓ
f
l
+
ℓ
m
s
−
s
s
i
m
+
ℓ
i
o
u
\ell_{s e g}=\ell_{f l}+\ell_{m s-s s i m}+\ell_{i o u}
ℓseg=ℓfl+ℓms−ssim+ℓiou
2.4 Classification-guided Module (CGM)
在这个模块中,主要是利用分类任务来解决由于较浅层中背景噪声等残留信息导致过分割的现象。CGM的具体结果如下图所示:

如图3所示,最深层次的二维张量 X E n 5 X_{E n}^{5} XEn5 经过一系列的操作包括dropout、1*1卷积、maxpooling、sigmoid,最后有两个值代表有/没有器官的概率。利用最丰富的语义信息,分类结果可以进一步指导每一个切分侧边输出两个步骤。首先,在Argmax函数的帮助下,将二维张量转化为 { 0 , 1 } \{0,1\} {0,1} 的单个输出,表示有/没有器官。随后,我们将单个分类输出与侧分割输出相乘。由于二分类任务的简单性,该模块通过优化交叉熵损失函数,轻松获得准确的分类结果,避免对非器官图像过分割。
从图3可以看出,分类部分主要是利用第五层,第五层是尺度最大的层,分类结果相对与其它层肯定会粗糙一些,因为用第五层判断第一层是不是器官,必然会有上采样或是第一层下采样的过程。但是,同样因为这个原因,第五层分类不会受到太多细节信息的影响,反而会使分类的区域定位也更加准确,这是一个非常巧妙的设计。
3、总结
UNet3+的优点和主要贡献在文章中都穿插讲述了,在总结部分主要提一下我自在实际应用中遇到的一些问题。
- 输入图像大小问题。UNet3+在编码部分采用的是无重叠的最大池化,这就要求图像下采样过程中的尺寸必须是偶数,在实际操作中可以先考虑最后一层(第5层),例如从下倒上反推依次为8、16、32、64、128。
- loss应用问题。作者使用了focal损失函数 ℓ f l \ell_{f l} ℓfl, MS-SSIM损失函数 ℓ m s − s s i m \ell_{m s-s s i m} ℓms−ssim和IoU损失函数 ℓ i o u \ell_{i o u} ℓiou的混合损失函数,但是我在实际使用中并没有严格遵守论文的loss,而是对五层输出的loss进行了加权操作并以第一层的loss为主。当然,总体效果还是不错的。
- 数据问题。由于自己项目中的图像质量总体偏差,因此原始数据进行了图像增强(数字图像处理定义中的增强,而不是增加样本)。从处理前后的数据训练结果对比来看,提高了3个百分点。
参考:https://zhuanlan.zhihu.com/p/136164721
更多推荐
 已为社区贡献5条内容
已为社区贡献5条内容







所有评论(0)