轮胎侧偏角、侧向力分析说明
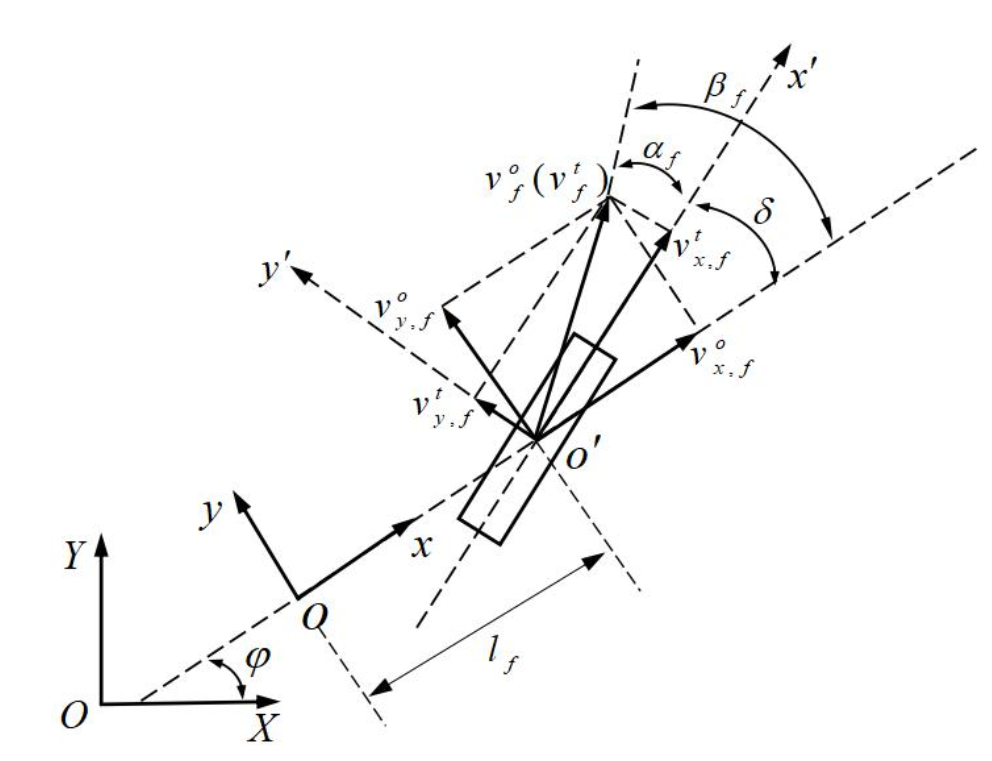
如图所示：图中：X - O - Y为全局直角坐标系；x - o - y为车身直角坐标系，其中：o为车辆质心，x为车头朝向；*x’ - o’ - y’*为前轮直角坐标系，其中：o为前轮转向中心，*x’*为轮胎前进方向；φ为航向角；δ为前轮转向角。下面重点对侧偏角进行说明：侧偏角是指纵向速度与合速度之间的夹角，图中：βf~为前轮在x - o - y坐标系下的侧偏角：...
文章共15,063字 · 阅读需要大约51分钟
如图所示：
图中：
X
−
O
−
Y
X - O - Y
X−O−Y 为全局直角坐标系；
x
−
o
−
y
x - o - y
x−o−y 为车身直角坐标系，其中：
o
o
o 为前轮转向中心，
x
x
x 为车头朝向；
x
′
−
o
′
−
y
′
x' - o' - y'
x′−o′−y′ 为前轮直角坐标系，其中：
o
′
o'
o′ 为前轮转向中心，
x
′
x'
x′ 为轮胎前进方向；
φ
\varphi
φ 为航向角；
δ
\delta
δ 为前轮转角。
侧偏角是指纵向速度和合速度之间的夹角，
x
x
x 轴上方为正，下方为负。在不同的坐标系中，同一点的侧偏角并不相同，其计算方式为对应坐标系下的侧向速度除以纵向速度然后取反正切，正负号根据对应坐标系的
x
x
x 轴进行判断。例如图中：
β
f
\beta_f
βf 为前轮中心
o
′
o'
o′ 在
x
−
o
−
y
x - o - y
x−o−y 坐标系下的侧偏角，符号为正：
β
f
=
arctan
v
y
,
f
o
v
x
,
f
o
\beta_f = \arctan \frac{v_{y,f}^o}{v_{x,f}^o}
βf=arctanvx,fovy,fo
α
f
\alpha_f
αf 为前轮中心
o
′
o'
o′ 在
x
′
−
o
′
−
y
′
x' - o' - y'
x′−o′−y′ 坐标系下的侧偏角，符号为正：
α
f
=
arctan
v
y
,
f
t
v
x
,
f
t
\alpha_f = \arctan \frac{v_{y,f}^t}{v_{x,f}^t}
αf=arctanvx,ftvy,ft
(上标 o o o 表示在 x − o − y x - o - y x−o−y 坐标系中的速度矢量，上标 t t t 表示在 x ′ − o ′ − y ′ x' - o' - y' x′−o′−y′ 坐标系中的速度矢量)
将点
o
′
o'
o′ 在
x
−
o
−
y
x - o - y
x−o−y 坐标系下的速度转换到
x
′
−
o
′
−
y
′
x' - o' - y'
x′−o′−y′ 坐标系中，得：
v
x
,
f
t
=
v
x
,
f
o
⋅
cos
δ
+
v
y
,
f
o
⋅
sin
δ
,
v
y
,
f
t
=
v
y
,
f
o
⋅
cos
δ
−
v
x
,
f
o
⋅
sin
δ
,
\begin{matrix} v_{x,f}^t = v_{x,f}^o \cdot \cos \delta \ + \ v_{y,f}^o \cdot \sin \delta, \\ \\ v_{y,f}^t = v_{y,f}^o \cdot \cos \delta \ - \ v_{x,f}^o \cdot \sin \delta, \end{matrix}
vx,ft=vx,fo⋅cosδ + vy,fo⋅sinδ,vy,ft=vy,fo⋅cosδ − vx,fo⋅sinδ,
综合上述表达式，得：
α f = arctan v y , f o ⋅ cos δ − v x , f o ⋅ sin δ v x , f o ⋅ cos δ + v y , f o ⋅ sin δ = arctan v y , f o v x , f o − tan δ 1 + v y , f o v x , f o ⋅ tan δ = arctan tan β f − tan δ 1 + tan β f ⋅ tan δ = β f − δ \alpha_f = \arctan \frac{v_{y,f}^o \cdot \cos \delta \ - \ v_{x,f}^o \cdot \sin \delta}{v_{x,f}^o \cdot \cos \delta \ + \ v_{y,f}^o \cdot \sin \delta} = \arctan \frac{\frac{v_{y,f}^o}{v_{x,f}^o} \ - \ \tan \delta}{1 \ + \ \frac{v_{y,f}^o}{v_{x,f}^o} \cdot \tan \delta} = \arctan \frac{\tan \beta_f \ - \ \tan \delta}{1 \ + \ \tan \beta_f \cdot \tan \delta} = \beta_f - \delta αf=arctanvx,fo⋅cosδ + vy,fo⋅sinδvy,fo⋅cosδ − vx,fo⋅sinδ=arctan1 + vx,fovy,fo⋅tanδvx,fovy,fo − tanδ=arctan1 + tanβf⋅tanδtanβf − tanδ=βf−δ
对于轮胎侧向力的计算，采用的是相对于轮胎坐标系下的侧偏角 ( α f \alpha_f αf )，在纯侧滑的情况下，轮胎侧向力与侧偏角的关系曲线如下图所示，可以看出，轮胎侧向力与侧偏角的符号是相反的。如果侧向力采用近似线性计算，则侧偏刚度往往取侧偏角为 0 0 0 处的斜率 − C f -C_f −Cf，从而计算得到侧向力为：
F y , f = − C f ⋅ α = C f ⋅ ( δ − β f ) F_{y,f} = -C_f \cdot \alpha = C_f \cdot (\delta \ - \ \beta_f) Fy,f=−Cf⋅α=Cf⋅(δ − βf)
在评论区中有朋友提到这样的问题：在某些文章或者书本绘制的示意图中，侧偏角绘制在前轮转角内，如下图所示，但是无论侧偏角在前轮转角内侧还是外侧，最终计算侧向力的表达式相同。造成这种殊途同归的情况，个人认为原因在于应用的侧偏角和侧向力的相关曲线不同。下面讲述一下个人的理解。
依据上图所示情况，可得：
α f = δ − β f \alpha_f = \delta \ - \ \beta_f αf=δ − βf
这与上文中推导的侧偏角 (
α
f
\alpha_f
αf ) 正好相差一个负号。
仍然约定侧偏角在
x
x
x 轴上方为正，下方为负。依据上文中的推导过程，同理可得：
β f = arctan v y , f o v x , f o , α f = arctan v y , f t v x , f t , v x , f t = v x , f o ⋅ cos δ + v y , f o ⋅ sin δ , v y , f t = v x , f o ⋅ sin δ − v y , f o ⋅ cos δ , \begin{matrix} \beta_f = \arctan \frac{v_{y,f}^o}{v_{x,f}^o}, \\ \\ \alpha_f = \arctan \frac{v_{y,f}^t}{v_{x,f}^t}, \\ \\ v_{x,f}^t = v_{x,f}^o \cdot \cos \delta \ + \ v_{y,f}^o \cdot \sin \delta, \\ \\ v_{y,f}^t = v_{x,f}^o \cdot \sin \delta \ - \ v_{y,f}^o \cdot \cos \delta, \end{matrix} βf=arctanvx,fovy,fo,αf=arctanvx,ftvy,ft,vx,ft=vx,fo⋅cosδ + vy,fo⋅sinδ,vy,ft=vx,fo⋅sinδ − vy,fo⋅cosδ,
综合上述表达式，得：
α f = arctan v x , f o ⋅ sin δ − v y , f o ⋅ cos δ v x , f o ⋅ cos δ + v y , f o ⋅ sin δ = arctan tan δ − v y , f o v x , f o 1 + v y , f o v x , f o ⋅ tan δ = arctan tan δ − tan β f 1 + tan β f ⋅ tan δ = δ − β f \alpha_f = \arctan \frac{v_{x,f}^o \cdot \sin \delta \ - \ v_{y,f}^o \cdot \cos \delta}{v_{x,f}^o \cdot \cos \delta \ + \ v_{y,f}^o \cdot \sin \delta} = \arctan \frac{ \tan \delta \ - \ \frac{v_{y,f}^o}{v_{x,f}^o}}{1 \ + \ \frac{v_{y,f}^o}{v_{x,f}^o} \cdot \tan \delta} = \arctan \frac{\tan \delta \ - \ \tan \beta_f}{1 \ + \ \tan \beta_f \cdot \tan \delta} = \delta - \beta_f αf=arctanvx,fo⋅cosδ + vy,fo⋅sinδvx,fo⋅sinδ − vy,fo⋅cosδ=arctan1 + vx,fovy,fo⋅tanδtanδ − vx,fovy,fo=arctan1 + tanβf⋅tanδtanδ − tanβf=δ−βf
在这种情况下，应该对应如下侧偏角与侧向力关系曲线，而不是上文给出的曲线，所以对应的近似线性侧偏刚度为 C f C_f Cf，从而计算得到侧向力为：
F y , f = C f ⋅ α f = C f ⋅ ( δ − β f ) F_{y,f} = C_f \cdot \alpha_f = C_f \cdot (\delta \ - \ \beta_f) Fy,f=Cf⋅αf=Cf⋅(δ − βf)
旨在为数千万中国开发者提供一个无缝且高效的云端环境，以支持学习、使用和贡献开源项目。
更多推荐
26
0- 0
已为社区贡献1条内容
所有评论(0)