文章首发于 2020-11-17

知乎文章:数据结构（C语言）-哈夫曼（Huffman）树编码译码操作

作者：落雨湿红尘（也是我o）

导语

本文使用C语言。对某一输入的字符串，如何对其构造哈夫曼（Huffman）树，并由此树的到字符串中每一个字符的哈夫曼编码

本文哈夫曼树和哈夫曼编码采用顺序存储结构实现

哈夫曼树

给定N个权值作为N个叶子结点，构造一棵二叉树，若该树的带权路径长度达到最小，称这样的二叉树为最优二叉树，也称为哈夫曼树(Huffman Tree)。哈夫曼树是带权路径长度最短的树，权值较大的结点离根较近。

                                               

                                                                                          哈夫曼树，图片来源百度百科

哈夫曼编码

在数据通信中，需要将传送的文字转换成二进制的字符串，用0，1码的不同排列来表示字符。例如，需传送的报文为“AFTER DATA EAR ARE ART AREA”，这里用到的字符集为“A，E，R，T，F，D”，各字母出现的次数为{8，4，5，3，1，1}。

现要求为这些字母设计编码。要区别6个字母，最简单的二进制编码方式是等长编码，固定采用3位二进制，可分别用000、001、010、011、100、101对“A，E，R，T，F，D”进行编码发送，当对方接收报文时再按照三位一分进行译码。显然编码的长度取决报文中不同字符的个数。若报文中可能出现26个不同字符，则固定编码长度为5

然而，传送报文时总是希望总长度尽可能短。在实际应用中，各个字符的出现频度或使用次数是不相同的，如A、B、C的使用频率远远高于X、Y、Z，自然会想到设计编码时，让使用频率高的用短码，使用频率低的用长码，以优化整个报文编码

为使不等长编码为前缀编码(即要求一个字符的编码不能是另一个字符编码的前缀)，可用字符集中的每个字符作为叶子结点生成一棵编码二叉树，为了获得传送报文的最短长度，可将每个字符的出现频率作为字符结点的权值赋予该结点上，显然字使用频率越小权值越小，权值越小叶子就越靠下，于是频率小编码长，频率高编码短，这样就保证了此树的最小带权路径长度效果上就是传送报文的最短长度

因此，求传送报文的最短长度问题转化为求由字符集中的所有字符作为叶子结点，由字符出现频率作为其权值所产生的哈夫曼树的问题。利用哈夫曼树来设计二进制的前缀编码，既满足前缀编码的条件，又保证报文编码总长最短，该前缀编码称为哈夫曼编码

                                          

                                                                             哈夫曼编码

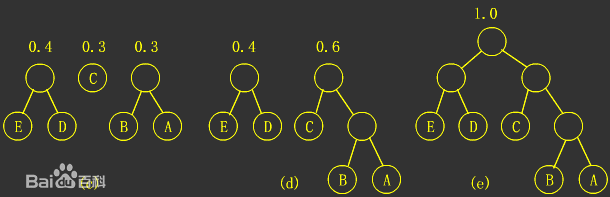
如上图所示，对于一个字符串“AAABBCCCDDDDE” 来说，很容易知道每个字符出现的频次{3，2，3，4，1}。根据频次，每次选出频次最小的两个结点进行组合，频次相加得到父结点。不断重复此过程，直到产生一颗哈夫曼树。

通过该哈夫曼树，我们可以得到每个字符的哈夫曼编码 A=10，B=001,C=01,D=11,E=000。容易证明，每个字符的编码都是前缀编码

C语言实现哈夫曼编码

网上许多大佬实现哈夫曼树的结点都是采用链式存储结构，而实现哈夫曼编码则是采用指针。

那鄙人就使用顺序存储结构来实现哈夫曼树结点，给大家提供一些思路吧

哈夫曼结点，放在一个数组中，即 HNodeType HuffNodes[]

typedef struct{        //Huffman树结点结构体
    float weight;      //结点权值，这里是字符出现的频率，及频次/字符种类数
    char ch_value;     //该节点对应的字符
    int parent;        //父结点位置索引，初始-1
    int lchild;        //左孩子位置索引，初始-1
    int rchild;        //右孩子位置索引，初始-1
} HNodeType;

哈夫曼编码结构，也采用顺序存储结构（数组）

typedef struct{        //Huffman编码结构体
    int bit[MAXBIT];   //该字符的哈夫曼编码
    int start;         //该编码在数组bit中的开始位置
    char ch_value;     //对应字符
} HCodeType;

接受字符串

void str_input(char str[]) {
    printf("请输入任意子字符串:\n");
    //输入可包含空格的字符串，输入字符串存放在str中
    gets(str);
}

统计字符频次 

int TextStatistics(char text[], char ch[], float weight[], int *length) {
    //统计每种字符的出现频次，返回出现的不同字符的个数ch_index
    //出现的字符存放在ch中，对应字符的出现频次存放在weight中, ch_index为ch中字符种类数
    //length为text长度

	int text_index = 0;  //text字符串索引
	int ch_index = 0;	 //计字符数组增加索引，仅用于出现不同字符时，将该字符加入到ch[]中。仅自增 
	
	int weight_index = 0;//频数更新索引。用于指定weight[]要更新频数的位置		 
				
	while(text[text_index]!='\0'){
		//查找ch中，是否存在字符text[text_index]，返回查到的第一个字符的位置 
		char* pos = strchr(ch,text[text_index]);
		
		//如果ch中无该字符。或者ch为空。就将text[text_index]加入到ch中 
		if(ch[0]=='\0'  || pos == NULL ){
	
			//加入到统计字符数组中
			ch[ch_index] = text[text_index];
							  		
			//新增一个字符的频数，当所有字符都统计完之后再计算频率 
			weight[ch_index] += 1;
			ch_index++;
			
		}
		
		//如果字符串中有该字符
		else{
			//找到该字符的索引位置，更新其频数 
			weight_index = pos - ch ; 
			weight[weight_index] += 1;

		}
		
		text_index++; 
	}
	ch[ch_index] = '\0';//添加结束符 
	//根据频数计算频率 
	int index=0;
	while(weight[index]!=0){
		weight[index]/=text_index;
		index++;
	}

	*length = text_index;  // 此时text_index即为源字符串text长度
	return ch_index; //最终 ch_index的值即为text字符串中不同字符的个数 
}

找到权值最小的两个结点

// 从 HuffNodes[0..range]中，找到最小的结点索引赋给s1,s2 。已经找到过的结点索引被储存在out[]中 
void select(HNodeType HuffNodes[],int range,int *s1,int *s2){
	//先找第一个最小值 。 
	float min1 = 5;

	for(int index1=0;index1<=range;index1++){
		
		if(HuffNodes[index1].weight < min1 && HuffNodes[index1].parent ==-1){
			//判断该结点是否被选过。如果该结点parent为0，则其为被选 									
				min1 = HuffNodes[index1].weight;
				*s1 = index1 ; 								
		} 	 
	}
	

	//找第2个最小值 	
	float min2 = 5;
	for(int index2=0;index2<=range ;index2++){		
		if(HuffNodes[index2].weight < min2 && HuffNodes[index2].parent ==-1 && index2!=*s1){			
			//判断该结点是否被选过。还要判断其是否被s1选了 													
				min2 = HuffNodes[index2].weight;
				*s2 = index2 ; 								
		} 	 
	}
	
} 

构造哈夫曼树

//构造一棵Huffman树，树结点存放在HuffNodes中
int HuffmanTree(HNodeType HuffNodes[], float weight[], char ch[], int n){
    //构造一棵Huffman树，树结点存放在HuffNodes中
    if(n>MAXLEAF) {
    	printf("超出叶结点最大数量!\n");
    	return -1;
	}
	if(n<=1) return -1;
	
	int m = 2*n-1;//结点总个数
	 
	int node_index = 0;
	//构造各叶节点	
	for(;node_index < n;node_index++){
	/*
		HuffNodes[node_index]->weight
        HuffNodes[node_index]->ch_value
		HuffNodes[node_index]->parent
		HuffNodes[node_index]->lchild
		HuffNodes[node_index]->rchild
	*/	
		HuffNodes[node_index] ={weight[node_index],ch[node_index],-1,-1,-1};		
	} 
	//构造非叶节点
	for(;node_index<m;node_index++)	HuffNodes[node_index] ={0,0,-1,-1,-1};		
	
	//构建Huffmantree
	 
	int s1,s2;//最小值索引
		
	for(int i = n;i < m;i++) {
		select(HuffNodes,i-1,&s1,&s2);
		HuffNodes[s1].parent = i;
		HuffNodes[s2].parent = i;
		HuffNodes[i].lchild = s1; 
		HuffNodes[i].rchild = s2;
		HuffNodes[i].weight = HuffNodes[s1].weight + HuffNodes[s2].weight;
	
	}

	return m-1; // HuffNodes数组中的最后一位，是Huffman树的根结点索引。
}

生成哈夫曼编码

void HuffmanCode(HNodeType HuffNodes[], HCodeType HuffCodes[], char ch[], int n) {
    //生成Huffman编码，Huffman编码存放在HuffCodes中（一个位置存储一个节点的哈夫曼编码，单个结点的哈夫曼编码在bit数组中)
    int start;
	for(int i =0 ;i<n;i++){
		start = n-2;  
        //字符ch[i]对应的Huffman编码（存储在bit数组中）起始位置，从右往左存.每个结点的哈夫曼编码的长度不超过（叶子结点个数n-1），因此bit数组只需要使用(n-1)的长度。
		//而哈夫曼编码是从哈夫曼树的叶子结点开始一直追溯到根结点按照左右赋予0/1值的，所以倒着编码，bit数组起始下标应该是(n-2)，每编码一位就减一
		HuffCodes[i].ch_value = ch[i];  // 存储该字符值
		for(int c = i , f=HuffNodes[i].parent ; f!=-1; c =f,f=HuffNodes[f].parent){//从叶子到根逆向求编码
			if(c == HuffNodes[f].lchild) HuffCodes[i].bit[start--]=0;
			else HuffCodes[i].bit[start--]=1;
		}
		HuffCodes[i].start = start+1;
	}
}

遍历哈夫曼树，使用队列递归方式，这里使用的中序遍历。前序遍历，后序遍历，都差不多

int MidOrderTraverse(HNodeType HuffNodes[], float result[], int root, int resultIndex) {
    //Huffman树的中序遍历，遍历结果存放在result中，返回下一个result位置索引   
    //根节点 为root 
	
	if (root!=-1){	
		resultIndex = MidOrderTraverse( HuffNodes,result,HuffNodes[root].lchild,resultIndex);
		result[resultIndex++] = HuffNodes[root].weight;
		resultIndex = MidOrderTraverse( HuffNodes,result,HuffNodes[root].rchild,resultIndex);															
	}
	
	return resultIndex;
}

encoding函数，用来把原始的输入字符串转换为Huffman编码串

int encoding(HCodeType HuffCodes[],char text[],char ch[],int n, int length, int coding_str[]){
	printf("输入的字符串为:%s\n",text);
	printf("其对应Huffman编码为（逗号分割版本）:\n");
	int coding_str_idx = 0;  //编码串索引
	for(int text_idx=0; text_idx<length; text_idx++){//从左到右遍历原字符串中各字符
		
		char* pos = strchr(ch,text[text_idx]);  //查找ch中，字符text[text_idx]索引
		// 字符text[text_idx]对应于ch[pos - ch]
		//其对应的Huffman编码，即保存在HuffCodes[pos - ch].bit中
	    for(int j = HuffCodes[pos - ch].start; j < n-1; j++){
	    	printf("%d", HuffCodes[pos - ch].bit[j]);
	    	coding_str[coding_str_idx++] = HuffCodes[pos - ch].bit[j];
	    }
	    printf(",");
	}
	printf("\n");
	return coding_str_idx;  // 编码串长度
}

译码方法，时间复杂度O(n)

//对Huffman编码串coding_str进行译码。res_str为译码结果
int decoding(HNodeType HuffNodes[], int coding_str[],int length, int root, char res_str[]){
	//从左到右遍历编码串，同时查找Huffman树（从根结点开始）；
	//编码串出现0（1），则查看Huffman树左（右）孩子结点，验证其是否为叶子结点。若否，则继续此步骤；
	//若是，则可译出该字符，并再从根结点开始查找。
	int tree_idx = root;  //Huffman树节点索引
	int code_idx = 0; //Huffman编码串索引
	int res_idx = 0;  //译码结果索引
	while(code_idx < length){
	 	while(HuffNodes[tree_idx].lchild != -1 and HuffNodes[tree_idx].rchild != -1){ //验证是否为叶子节点
	 		if(coding_str[code_idx] == 0){  //查看左孩子结点
	 			tree_idx = HuffNodes[tree_idx].lchild;
	 		}
	 		else{  //查看右孩子结点
	 			tree_idx = HuffNodes[tree_idx].rchild;
	 		}
	 		code_idx +=1;
	 	}
	 	res_str[res_idx++] = HuffNodes[tree_idx].ch_value;
	 	tree_idx = root;
	}
	return res_idx;
}

主函数

#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#define MAXVALUE  100000        //输入文本最大字符个数
#define MAXLEAF   256           //最大叶结点个数，即最大不同字符个数
#define MAXBIT    MAXLEAF-1     //编码最大长度
#define MAXNODE   MAXLEAF*2-1   //最大结点个数
int main(){
	
    HNodeType HuffNodes[MAXNODE];   // 定义一个结点结构体数组
    HCodeType HuffCodes[MAXLEAF];   // 定义一个编码结构体数组
    char text[MAXVALUE+1], ch[MAXLEAF];
    float weight[MAXLEAF], result[MAXNODE];
    int i, j, n, resultIndex, length;

    str_input(text);
	
	// 1.统计字符总数n，输入长度length
    n = TextStatistics(text, ch, weight, &length);
	if(n==1){
		printf("只有一种字符，不用编码了。请多输入几种字符\n");
		return 0;
	}
	
    // 2.构造哈夫曼树和哈夫曼编码
    int root = HuffmanTree(HuffNodes, weight, ch, n);
    if (root<0)
    {
    	printf("Huffman树构造失败");
    	return 0;
    }
    HuffmanCode(HuffNodes, HuffCodes, ch, n);

    for (i=0; i<n; i++) { 
        printf("%c的Huffman编码是：", ch[i]);

        for(j=HuffCodes[i].start; j<n-1; j++)
            printf("%d", HuffCodes[i].bit[j]);

        printf("\n");
    }
    
	
    // 3.输出Huffman树的中序遍历结果
    resultIndex = MidOrderTraverse(HuffNodes, result, root, 0);
    printf("\nHuffman树的中序遍历结果是：");
	
    for (i=0; i<resultIndex; i++){
        if (i < resultIndex-1)
            printf("%.4f, ", result[i]);
        else
            printf("%.4f\n\n", result[i]);
	}

	// 4.转换为Huffman编码
	int coding_str[MAXBIT*length];  //Huffman编码串
	int coding_length = encoding(HuffCodes,text,ch, n, length, coding_str);
	printf("其对应Huffman编码为（无分割版本）:\n");
	for (int i = 0; i < coding_length; i++){
		printf("%d", coding_str[i]);
	}
	printf("\n");

	// 5.译码过程
	char res_str[length];  //译码结果
	int res_length = decoding(HuffNodes, coding_str, coding_length, root, res_str);
	printf("Huffman译码结果为:");
	for (int i = 0; i < res_length; i++){
		printf("%c", res_str[i]);
	}
	printf("\n");
//	system("pause");
	return 0;
}

输出结果

以上代码，经过本人调试，没有看出问题来。若有问题，欢迎指正