回归分析(线性回归、逻辑回归)详解与 Python 实现
文章目录1. 回归分析概述1.1 基本概念1. 回归分析概述1.1 基本概念 回归分析是处理多变量间相关关系的一种数学方法。相关关系不同于函数关系,函数关系反应变量间严格依存性,简单说就是一个自变量对应一个因变量。而相关分析中,对自变量的每一个取值,因变量可以有多个数值与之对应。在统计上,研究相关关系可以运用回归分析和相关分析。 当自变量为非随机变量而因变量为随机变量时,它们的关系分析...
文章目录
1. 回归分析概述
回归分析是处理多变量间相关关系的一种数学方法。相关关系不同于函数关系,函数关系反应变量间严格依存性,简单说就是一个自变量对应一个因变量。而相关分析中,对自变量的每一个取值,因变量可以有多个数值与之对应。在统计上,研究相关关系可以运用 回归分析 和 相关分析。
当自变量为非随机变量而因变量为随机变量时,它们的关系分析成为 回归分析。当自变量和因变量都是随机变量时,它们的关系分析称为 相关分析。回归分析和相关分析往往不加区分。广义上说,相关分析包括回归分析,但是严格说两者是有区别的。
具有相关关系的两个变量 ξ 和 η(ξ:克西、η :伊塔 ),它们之间虽然存在着密切的关系,但不能由一个变量精确地求出另一个变量的值。通常选用 ξ = x 时 η 的数学期望作为对应 ξ = x 时 η 的代表值,因此它反映 ξ = x 条件下 η 取值的平均水平。这样的对应关系称为 回归关系。根据回归分析可以建立变量间的数学表达式,称为 回归方程。回归方程反映自变量在固定条件下因变量的平均状态变化情况。
具有相关关系的变量之间虽然具有某种不确定性,但是通过对现象的不断观察可以探索出它们之间的统计规律,这类统计规律称为 回归关系。有关回归关系理论、计算和分析称为 回归分析。
回归分析可以分为 线性回归分析 和 逻辑回归分析。
2. 线性回归
线性回归就是将输入项分别乘以一些常量,再将结果加起来得到输出。线性回归包括一元线性回归和多远线性回归。
线性回归模型的优缺点
- 优点:快速;没有调节参数;可轻易解释;了理解。
- 缺点:相比其他复杂一些的模型,其预测准确率不高,因为它假设特征和响应之间存在确定的线性关系,这种假设对于非线性的关系,线性模型显然不能很好地进行数据建模。
2.1 简单线性回归分析
线性回归分析中,如果仅有一个自变量与一个因变量,且其关系大致可以用一条直线表示,则称之为 简单线性回归分析。
如果发现因变量 Y 和自变量 X 之间存在高度的正相关,则可以确定一条直线方程,使得所有的数据点尽可能接近这条拟合的直线。
Y
=
a
+
b
x
Y=a+bx
Y=a+bx
其中
Y
Y
Y 为因变量,
a
a
a 为截距,
b
b
b 为相关系数,
x
x
x 为自变量。
2.2 多元线性回归分析
多元线性回归分析是简单线性回归分析的推广,指的是多个因变量对多个自变量的回归分析。其中最常用的是只限于一个因变量但有多个自变量的情况,也叫做多重回归分析。
Y
=
a
+
b
1
X
1
+
b
2
X
2
+
b
3
X
3
+
⋯
+
b
k
X
k
Y = a + b_1X_1+ b_2X_2 + b_3X_3 + \cdots+ b_kX_k
Y=a+b1X1+b2X2+b3X3+⋯+bkXk
其中,
a
a
a 代表截距,
b
1
,
b
2
,
b
3
,
⋯
,
b
k
b_1, b_2 , b_3 , \cdots, b_k
b1,b2,b3,⋯,bk 为回归系数。
2.3 非线性回归数据分析
数据挖掘中常用的一些非线性回归模型:
- 渐进回归模型
Y = a + b e − r X Y = a + be^{-rX} Y=a+be−rX - 二次曲线模型
Y = a + b 1 X + b 2 X 2 Y = a + b_1X+ b_2~X^2 Y=a+b1X+b2 X2 - 双曲线模型
Y = a + b X Y=a+\frac{b}{X} Y=a+Xb
3. 用 python 实现一元线性回归
一个简单的线性回归的例子就是房子价值预测问题。一般来说,房子越大,房屋的价值越高。
数据集:input_data.csv
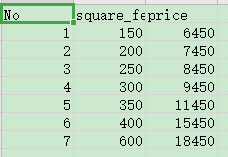
说明:
No:编号
square_feet:平方英尺
price:价格(元/平方英尺)
代码如下:
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
from sklearn import linear_model
# 读取数据的函数
def get_data(file_name):
data = pd.read_csv(file_name)
X = []
Y = []
for square_feet, price in zip(data["square_feet"],data["price"]):
X.append([square_feet])
Y.append(price)
return X,Y
# 建立线性模型,并进行预测
def get_linear_model(X, Y, predict_value):
model = linear_model.LinearRegression().fit(X,Y)
pre = model.predict(predict_value)
predictions = {}
predictions["intercept"] = model.intercept_ # 截距值
predictions["coefficient"] = model.coef_ # 回归系数(斜率)
predictions["predictted_value"] = pre
return predictions
# 显示线性拟合模型结果
def show_linear_line(X,Y):
model = linear_model.LinearRegression().fit(X,Y)
plt.scatter(X,Y)
plt.plot(X,model.predict(X),color="red")
plt.title("Prediction of House")
plt.xlabel("square feet")
plt.ylabel("price")
plt.show()
# 定义主函数
def main():
X, Y = get_data("input_data.csv")
print("X:",X)
print("Y:",Y)
predictions = get_linear_model(X,Y,[[700]])
print(predictions)
show_linear_line(X,Y)
main()
结果截图:
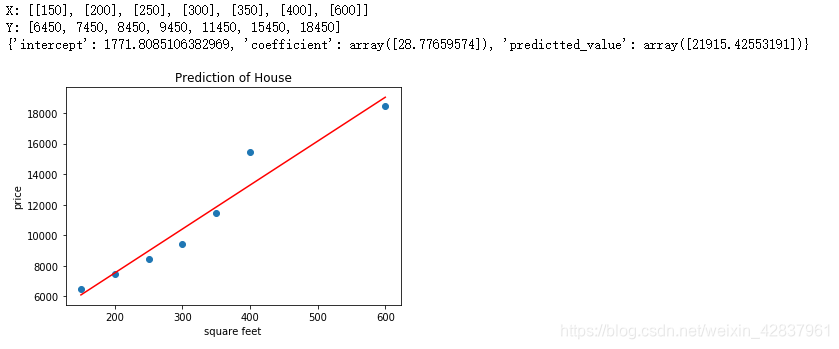
4. 用 python 实现多元线性回归
当结果值影响因素有多个时,可以采用多元线性回归模型。例如:商品的销售额可能与电视广告投入、收音机广告投入和报纸广告投入有关系,可以有:
S
a
l
e
s
=
β
0
+
β
1
T
V
+
β
2
R
a
d
i
o
+
β
3
N
e
w
s
p
a
p
e
r
Sales = β_0+ β_1TV + β_2Radio + β_3Newspaper
Sales=β0+β1TV+β2Radio+β3Newspaper
数据集:Advertising.csv
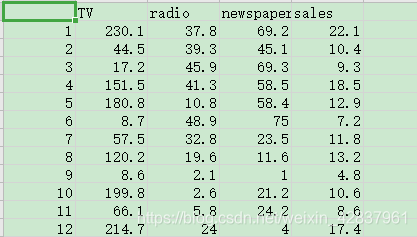
代码如下:
import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import explained_variance_score,\
mean_absolute_error,mean_squared_error,median_absolute_error,r2_score
# 1.读取数据
data = pd.read_csv("Advertising.csv")
print(data.head())
print("shape:",data.shape)
# 2.分析数据
sns.pairplot(data, x_vars=["TV","radio","newspaper"], y_vars="sales",height=5,aspect=0.8,kind="reg")
plt.show()
# 3.建立线性回归模型
# (1)使用 pandas 构建 X(特征向量)和 y(标签列)
feature_cols = ["TV","radio","newspaper"]
X = data[feature_cols]
y = data["sales"]
# (2)构建训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X,y,random_state=1) # 25% 测试
# (3)构建线性回归模型并训练
model = LinearRegression().fit(X_train,y_train)
# (4)输出模型结果
print("截距:",model.intercept_)
coef = zip(feature_cols, model.coef_)
print("回归系数:",list(coef))
# 4. 预测
y_pred = model.predict(X_test)
# 5. 评价
# 这个是自己写函数计算
sum_mean = 0
for i in range(len(y_pred)):
sum_mean += (y_pred[i] - y_test.values[i])**2
sum_erro = np.sqrt(sum_mean/len(y_test))
print("均方根误差(RMSE):",sum_erro)
# 这个是调用已有函数,以后就直接用
print("平均绝对误差(MAE):",mean_absolute_error(y_test,y_pred))
print("均方误差(MSE):",mean_squared_error(y_test,y_pred))
print("中值绝对误差:",median_absolute_error(y_test,y_pred))
print("可解释方差:",explained_variance_score(y_test,y_pred))
print("R方值:",r2_score(y_test,y_pred))
# 绘制 ROC 曲线
plt.plot(range(len(y_pred)),y_pred,"b",label="predict")
plt.plot(range(len(y_pred)),y_test,"r",label="test")
plt.xlabel("number of sales")
plt.ylabel("value of sales")
plt.legend(loc="upper right")
plt.show()
结果截图:
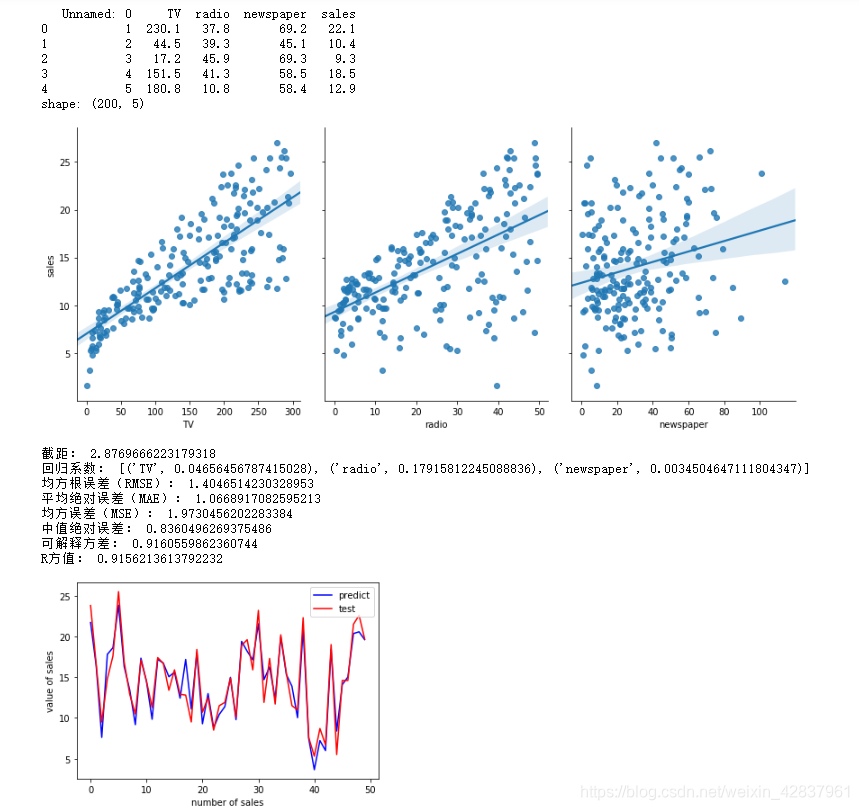
说明:
- pandas 两个主要的数据结构是 Series 和 DataFrame;Series 类似于一维数组,它由一组数据及一组与之有关的数据标签(及索引)组成;DataFrame 是一个表格型的数据结构,它含有一组有序的列,每列可以是不同的值类型。DataFrame 既有行索引也有列索引。
- 在分析数据时,使用了 seaborn 包,这个包数据可视化效果更好。其实 seaborn 包 也属于 Matplotlib 的内部包,只是需要单独安装。
- scikit-learn 要求 X 是一个特征矩阵,y 是一个 Numpy 向量。因此,X 可以是 pandas 的 DataFrame,y 可以是 pandas 的 Series。
- 对于分类问题,评价测度是准确率,但其不适用于回归问题,因此使用针对连续数值的评价测度(evaluation metrics)。
5. 逻辑回归
逻辑回归也被称为广义线性回归模型,它与线性回归模型的形式基本上相同,最大的区别就在于它们的因变量不同,如果是连续的,就是多重线性回归;如果是二项分布,就是逻辑回归(Logistic);逻辑回归实际上是一种分类方法,主要用于二分类问题(即输出只有两种,分别代表两个类别)。
逻辑回归的过程:面对一个回归或者分类问题,建立代价函数,然后通过优化方法迭代求解出最优的模型参数,然后测试验证这个求解模型的好坏。
逻辑回归的优缺点
- 优点:速度快,适合二分类问题;简单。易于理解,可以直接看到各个特征的权重;能容易地更新模型吸收新的数据。
- 缺点:对数据和场景的适应能力有局限性,不如决策树算法强。
逻辑回归的常规步骤
- 寻找 h h h 函数(预测函数)
- 构造 J J J 函数(损失函数)
- 想办法使 J J J 函数最小并求得回归参数 (θ)
5.1 构造预测函数(假设函数)
二类分类问题的概率与自变量之间的关系图形往往是一个 S 型曲线,采用 sigmoid 函数实现,函数形式:
g
(
z
)
=
1
1
+
e
−
z
g(z) =\frac{1}{1 + e^{-z}}
g(z)=1+e−z1

对于线性边界情况,边界形式如下:
z
=
θ
T
x
=
θ
0
x
0
+
θ
1
x
1
+
⋯
+
θ
n
x
n
=
∑
i
=
0
n
θ
i
x
i
z=θ^Tx=θ_0x_0+θ_1x_1+\cdots +θ_nx_n = \sum_{i=0}^{n} {θ_ix_i}
z=θTx=θ0x0+θ1x1+⋯+θnxn=i=0∑nθixi
说明:
(
x
0
,
x
1
,
…
,
x
n
)
(x_0,x_1,\ldots,x_n)
(x0,x1,…,xn) 为输入数据的特征,
(
θ
0
,
θ
1
,
…
,
θ
n
)
(θ_0,θ_1,\ldots,θ_n)
(θ0,θ1,…,θn) 为回归系数,也可以理解为权重
w
w
w。
最佳参数:
θ
=
[
θ
0
,
θ
1
,
θ
2
,
…
,
θ
n
]
T
θ=[θ_0,θ_1,θ_2,\ldots,θ_n]^T
θ=[θ0,θ1,θ2,…,θn]T
构造预测函数为:
h
θ
(
x
)
=
g
(
θ
T
x
)
=
1
1
+
e
−
θ
T
x
h_θ(x)=g(θ^Tx)=\frac{1}{1 + e^{-θ^Tx}}
hθ(x)=g(θTx)=1+e−θTx1
sigmod 函数输出是介于 (0,1) 之间的,中间值是 0.5。
h
θ
(
x
)
h_θ(x)
hθ(x) 的输出也是介于 (0,1) 之间的,也就表明了数据属于某一类别的概率。例如,
h
θ
(
x
)
<
0.5
h_θ(x)<0.5
hθ(x)<0.5 则说明当前数据属于 A 类;
h
θ
(
x
)
>
0.5
h_θ(x)>0.5
hθ(x)>0.5 则说明当前数据属于 B 类。所以 sigmod 函数看成样本数据的概率密度函数。
函数
h
(
x
)
h(x)
h(x) 的值有特殊的含义,它表示结果取 1 的概率,因此对于输入
x
x
x 分类结果为类别 1 和类别 0 的概率分别为:
p
(
y
=
1
∣
x
;
θ
)
=
h
θ
(
x
)
p(y=1|x;θ)=h_θ(x)
p(y=1∣x;θ)=hθ(x)
p
(
y
=
0
∣
x
;
θ
)
=
1
−
h
θ
(
x
)
p(y=0|x;θ)=1-h_θ(x)
p(y=0∣x;θ)=1−hθ(x)
5.2 构造损失函数
机器学习模型中把 单个样本 的预测值与真实值的差称为 损失,一般情况下,损失越小,模型越好(有可能存在 过拟合)。用于计算损失的函数称为 损失函数(Loss Function)。模型的每一次预测的好坏用损失函数度量。
代价函数 (Cost Function)是定义在整个训练集上的,是所有样本误差的平均,也就是损失函数的平均。
与多元线性回归所采用的最小二乘法的参数估计相对应,最大似然法是逻辑回归所采用的参数估计法。其原理是找到这样一个参数,可以让样本数据所包含的观察值被观察到的可能性最大。这种寻找最大可能性的方法需要反复计算,对计算能力有很高的要求。最大似然法的优点是大样本数据中参数的估计稳定、偏差小、估计方差小。
接下来使用概率论中极大似然估计的方法求解损失函数(需要大家有概率论和高数的知识储备,后面有说明):
首先得到概率函数为:
p
(
y
∣
x
;
θ
)
=
(
h
θ
(
x
)
)
y
(
1
−
h
θ
(
x
)
)
1
−
y
p(y|x;θ)=(h_θ(x))^y(1-h_θ(x))^{1-y}
p(y∣x;θ)=(hθ(x))y(1−hθ(x))1−y
因为样本数据(m 个)独立,所以它们的联合分布可以表示为各边际分布的乘积,取 似然函数为:
L
(
θ
)
=
∏
i
=
1
m
p
(
y
i
∣
x
i
;
0
)
=
∏
i
=
1
m
(
h
θ
(
x
i
)
)
y
i
(
1
−
h
θ
(
x
i
)
)
1
−
y
i
L(θ)=\prod_{i=1}^{m} {p(y_i|x_i;0)=\prod_{i=1}^{m} {(h_θ(x_i))^{y_i}(1-h_θ(x_i))^{1-y_i}}}
L(θ)=i=1∏mp(yi∣xi;0)=i=1∏m(hθ(xi))yi(1−hθ(xi))1−yi
取对数似然函数:
l
(
θ
)
=
log
L
(
θ
)
=
∑
i
=
1
m
(
y
i
log
h
θ
(
x
i
)
+
(
1
−
y
i
)
log
(
1
−
h
θ
(
x
i
)
)
)
l(θ)=\log L(θ)=\sum_{i=1}^{m}{(y_i\log h_θ(x_i)+(1-y_i)\log (1-h_θ(x_i)))}
l(θ)=logL(θ)=i=1∑m(yiloghθ(xi)+(1−yi)log(1−hθ(xi)))
最大似然估计就是要求使
l
(
θ
)
l(θ)
l(θ) 取最大值时的
θ
θ
θ,这里可以使用 梯度上升法 求解,求得的
θ
θ
θ 就是要求的最佳参数:
J
(
θ
)
=
−
1
m
l
(
θ
)
J(θ) = -\frac{1}{m}l(θ)
J(θ)=−m1l(θ)
基于最大似然估计推导得到的
C
o
s
t
Cost
Cost 函数和
J
J
J 函数如下:
C
o
s
t
(
h
θ
(
x
)
,
y
)
=
{
−
log
(
h
θ
(
x
)
)
,
if
y
=1
−
log
(
1
−
h
θ
(
x
)
)
,
if
y
=0
Cost(h_θ(x),y)=\begin{cases} -\log (h_θ(x)), & \text {if $y$ =1} \\ -\log (1-h_θ(x)), & \text{if $y$=0} \end{cases}
Cost(hθ(x),y)={−log(hθ(x)),−log(1−hθ(x)),if y =1if y=0
上面的分段函数可以合并为一条式子:
C
o
s
t
(
h
θ
(
x
)
,
y
)
=
−
y
log
(
h
θ
(
x
)
−
(
1
−
y
)
log
(
1
−
h
θ
(
x
)
)
)
Cost(h_θ(x),y)=-y\log(h_θ(x)-(1-y)\log(1-h_θ(x)))
Cost(hθ(x),y)=−ylog(hθ(x)−(1−y)log(1−hθ(x)))
J
(
θ
)
=
1
m
∑
i
=
1
m
C
o
s
t
(
h
θ
(
x
i
)
,
y
i
)
=
−
1
m
[
∑
i
=
1
m
(
y
i
log
h
θ
(
x
i
)
+
(
1
−
y
i
)
log
(
1
−
h
θ
(
x
i
)
)
)
]
J(θ)=\frac{1}{m}\sum_{i=1}^{m}Cost(h_θ(x_i),y_i) = -\frac{1}{m}[\sum_{i=1}^{m}{(y_i\log h_θ(x_i)+(1-y_i)\log (1-h_θ(x_i)))}]
J(θ)=m1i=1∑mCost(hθ(xi),yi)=−m1[i=1∑m(yiloghθ(xi)+(1−yi)log(1−hθ(xi)))]
说明:
- 梯度是求函数关于各个变量的偏导数,所以它代表函数值增长最快的方向。
g r a d ( f ( x , y ) ) = ∇ f ( x , y ) = [ ∂ ( x , y ) ∂ x , ∂ ( x , y ) ∂ y ] grad(f(x,y))=\nabla f(x,y)=[\frac{\partial(x,y)}{\partial x},\frac{\partial(x,y)}{\partial y}] grad(f(x,y))=∇f(x,y)=[∂x∂(x,y),∂y∂(x,y)] - 梯度上升算法求函数的最大值,梯度下降算法求函数的最小值。
- 梯度上升法迭代公式:
w : = w + α ∇ w f ( w ) w:=w+\alpha \nabla_wf(w) w:=w+α∇wf(w)
其中 α \alpha α 为步长,步长决定了梯度在迭代过程中,每一步沿梯度方向前进的长度。( α \alpha α 也称为 学习率)
梯度下降公式就是将 + 号改为 - 号。
5.3 梯度下降法求解最小值
因为要求损失函数 J ( θ ) J(\theta) J(θ) 最小值,所以采用梯度下降的方法。
1.
θ
θ
θ 更新过程
θ
:
=
θ
j
−
α
∂
∂
θ
j
J
(
θ
)
θ:=θ_j -α\frac{\partial}{\partial_{θ_j}}J(θ)
θ:=θj−α∂θj∂J(θ)
∂ ∂ θ j J ( θ ) = − 1 m ∑ i = 1 m [ y i 1 h θ ( x i ) ∂ ∂ θ j h θ ( x i ) − ( 1 − y i ) 1 1 − h θ ( x i ) ∂ ∂ θ j h θ ( x i ) ] = − 1 m ∑ i = 1 m [ y i 1 g ( θ T x i ) − ( 1 − y i ) 1 1 − g ( θ T x i ) ] ∂ ∂ θ j g ( θ T x i ) = − 1 m ∑ i = 1 m [ y i 1 g ( θ T x i ) − ( 1 − y i ) 1 1 − g ( θ T x i ) ] g ( θ T x i ) ( 1 − g ( θ T x i ) ) ∂ ∂ θ j θ T x i = − 1 m ∑ i = 1 m [ y i ( 1 − g ( θ T x i ) ) − ( 1 − y i ) g ( θ T x i ) ] x i j = − 1 m ∑ i = 1 m [ y i − g ( θ T x i ) ] x i j = − 1 m ∑ i = 1 m ( h θ ( x i ) − y i ) x i j \begin{aligned} \frac{\partial}{{\partial_θ}_j}J(θ) &= -\frac{1}{m}\sum_{i=1}^{m}{[y_i\frac{1}{h_θ(x_i)}\frac{\partial}{\partial_{θ_j}}h_θ(x_i)-(1-y_i)\frac{1}{1-h_θ(x_i)}\frac{\partial}{\partial_{θ_j}}h_θ(x_i)]} \\ &= -\frac{1}{m}\sum_{i=1}^{m}[y_i\frac{1}{g(θ^Tx_i)}-(1-y_i)\frac{1}{1-g(θ^Tx_i)}]\frac{\partial}{\partial_{θ_j}}g(θ^Tx_i) \\ &= -\frac{1}{m}\sum_{i=1}^{m}[y_i\frac{1}{g(θ^Tx_i)}-(1-y_i)\frac{1}{1-g(θ^Tx_i)}]g(θ^Tx_i)(1-g(θ^Tx_i))\frac{\partial}{\partial_{θ_j}}θ^Tx_i \\ &= -\frac{1}{m}\sum_{i=1}^{m}[y_i(1-g(θ^Tx_i))-(1-y_i)g(θ^Tx_i)]x_i^j \\ &= -\frac{1}{m}\sum_{i=1}^{m}[y_i-g(θ^Tx_i)]x_i^j \\ &= -\frac{1}{m}\sum_{i=1}^{m}(h_θ(x_i)-y_i)x_i^j \\ \end{aligned} ∂θj∂J(θ)=−m1i=1∑m[yihθ(xi)1∂θj∂hθ(xi)−(1−yi)1−hθ(xi)1∂θj∂hθ(xi)]=−m1i=1∑m[yig(θTxi)1−(1−yi)1−g(θTxi)1]∂θj∂g(θTxi)=−m1i=1∑m[yig(θTxi)1−(1−yi)1−g(θTxi)1]g(θTxi)(1−g(θTxi))∂θj∂θTxi=−m1i=1∑m[yi(1−g(θTxi))−(1−yi)g(θTxi)]xij=−m1i=1∑m[yi−g(θTxi)]xij=−m1i=1∑m(hθ(xi)−yi)xij
θ
θ
θ 更新过程可以写成:
θ
j
:
=
θ
j
−
α
1
m
∑
i
=
1
m
(
h
θ
(
x
i
)
−
y
i
)
x
i
j
θ_j:=θ_j-α\frac{1}{m}\sum_{i=1}^{m}(h_θ(x_i)-y_i)x_i^j
θj:=θj−αm1i=1∑m(hθ(xi)−yi)xij
2. 向量化
约定训练数据的矩阵形式如下,
x
x
x 的每一行为一条训练样本,而每一列为不同的特征取值:
x
=
[
x
1
⋮
x
m
]
=
[
x
10
⋯
x
1
n
⋮
⋱
⋮
x
m
0
⋯
x
m
n
]
,
y
=
[
y
1
⋮
y
m
]
,
θ
=
[
θ
0
⋮
θ
n
]
x= \begin{bmatrix} x_1 \\ \vdots \\ x_m \\ \end{bmatrix} = \begin{bmatrix} x_{10} & \cdots & x_{1n} \\ \vdots & \ddots & \vdots \\ x_{m0} & \cdots & x_{mn} \\ \end{bmatrix},y= \begin{bmatrix} y_1 \\ \vdots \\ y_m \\ \end{bmatrix} ,θ= \begin{bmatrix} θ_0 \\ \vdots \\ θ_n \\ \end{bmatrix}
x=⎣⎢⎡x1⋮xm⎦⎥⎤=⎣⎢⎡x10⋮xm0⋯⋱⋯x1n⋮xmn⎦⎥⎤,y=⎣⎢⎡y1⋮ym⎦⎥⎤,θ=⎣⎢⎡θ0⋮θn⎦⎥⎤
A
=
x
●
θ
=
[
x
10
⋯
x
1
n
⋮
⋱
⋮
x
m
0
⋯
x
m
n
]
●
[
θ
0
⋮
θ
n
]
=
[
θ
0
x
10
+
θ
1
x
11
+
…
+
θ
n
x
1
n
…
θ
0
x
m
0
+
θ
1
x
m
1
+
…
+
θ
n
x
m
n
]
A=x●θ= \begin{bmatrix} x_{10} & \cdots & x_{1n} \\ \vdots & \ddots & \vdots \\ x_{m0} & \cdots & x_{mn} \\ \end{bmatrix}● \begin{bmatrix} θ_0 \\ \vdots \\ θ_n \\ \end{bmatrix} = \begin{bmatrix} θ_0x_{10}+θ_1x_{11}+\ldots+ θ_nx_{1n}\\ \ldots\\ θ_0x_{m0}+θ_1x_{m1}+\ldots+ θ_nx_{mn}\\ \end{bmatrix}
A=x●θ=⎣⎢⎡x10⋮xm0⋯⋱⋯x1n⋮xmn⎦⎥⎤●⎣⎢⎡θ0⋮θn⎦⎥⎤=⎣⎡θ0x10+θ1x11+…+θnx1n…θ0xm0+θ1xm1+…+θnxmn⎦⎤
E
=
h
θ
(
x
)
−
y
=
[
g
(
A
1
)
−
y
1
⋮
g
(
A
m
)
−
y
m
]
=
[
e
1
⋮
e
m
]
=
g
(
A
)
−
y
E=h_θ(x)-y= \begin{bmatrix} g(A_1) -y_1 \\ \vdots \\ g(A_m) -y_m \\ \end{bmatrix} = \begin{bmatrix} e_1 \\ \vdots \\ e_m \\ \end{bmatrix} = g(A) -y
E=hθ(x)−y=⎣⎢⎡g(A1)−y1⋮g(Am)−ym⎦⎥⎤=⎣⎢⎡e1⋮em⎦⎥⎤=g(A)−y
g
(
A
)
g(A)
g(A) 的参数
A
A
A 为一列向量,所以实现
g
g
g 函数时要支持列向量作为参数,并返回列向量。
θ
θ
θ 的更新过程可以改为:
θ
j
:
=
θ
j
−
α
1
m
∑
i
=
1
m
(
h
θ
(
x
i
)
−
y
i
)
x
i
j
=
θ
j
−
α
1
m
∑
i
=
1
m
e
i
x
i
j
=
θ
j
−
α
1
m
x
T
E
θ_j:=θ_j-α\frac{1}{m}\sum_{i=1}^{m}(h_θ(x_i)-y_i)x_i^j=θ_j-α\frac{1}{m}\sum_{i=1}^{m}e_ix_i^j=θ_j-α\frac{1}{m}x^TE
θj:=θj−αm1i=1∑m(hθ(xi)−yi)xij=θj−αm1i=1∑meixij=θj−αm1xTE
3. 正则化
过拟合 即过分拟合了训练数据,使得模型的复杂度提高,泛化能力较差(对未知数据的预测能力)。
可以使用正则化解决过拟合问题,正则化是结构风险最小化策略的实现,是在经验风险上加一个正则化项或惩罚项。正则化一般是模型复杂度的单调递增函数,模型越复杂,正则化项就越大。
正则项可以采取不同的形式,在回归问题中取平方损失,就是参数的
L
2
L2
L2 范数,也可以取
L
1
L1
L1 范数。取平方损失时,模型的损失函数变为:
J
(
θ
)
=
1
2
m
∑
i
=
1
n
(
h
θ
(
x
i
)
−
y
i
)
2
+
λ
∑
j
=
1
n
θ
j
2
J(θ)=\frac{1}{2m}\sum_{i=1}^{n}(h_θ(x_i)-y_i)^2+λ\sum_{j=1}^{n}{θ_j}^2
J(θ)=2m1i=1∑n(hθ(xi)−yi)2+λj=1∑nθj2
说明:
- 系数乘以 1 2 \frac{1}{2} 21 是因为减小个别较大极端值对损失函数的影响,乘以一个小于 1 的系数,可以看做是减小噪声(极端值)。也可以是 1 3 \frac{1}{3} 31, 1 4 \frac{1}{4} 41,但一般选择 1 2 \frac{1}{2} 21。
- λ 是正则项系数:
- 如果它的值很大,说明对模型的复杂度惩罚大,对拟合数据的损失惩罚小,这样它就不会过分拟合数据,在训练数据上的偏差较大,在未知数据上的方差较小,可能出现欠拟合的现象。
- 如果它的值很小,说明比较注重对训练数据的拟合,在训练数据上偏差会小,但是可能导致过拟合。
正则化后的梯度下降算法
θ
θ
θ 的更新变为:
θ
j
:
=
θ
j
−
α
m
∑
i
=
1
m
(
h
θ
(
x
i
)
−
y
i
)
x
i
j
−
λ
m
θ
j
θ_j:=θ_j-\frac{α}{m}\sum_{i=1}^{m}(h_θ(x_i)-y_i)x_i^j-\frac{λ}{m}θ_j
θj:=θj−mαi=1∑m(hθ(xi)−yi)xij−mλθj
6. 用 Python 实现逻辑回归
数据集:data.csv
说明:一共 100 条数据,前两列是数据的两个特征,第三列是分类结果(标签列)
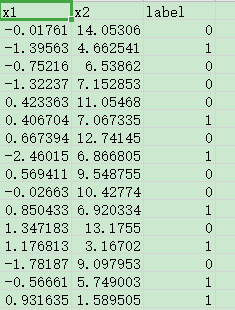
代码如下:
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
# 定义读取数据函数
def loadDateSet(filename):
df = pd.read_csv(filename) # 读取数据
m = df.shape[0] # m为数据条数
df["x0"] = np.ones((m,1)) # 为数据增加一列值为 1.0 的数据
data = df[["x0","x1","x2"]] # 为数据的特征 x0,x1,x2
label = df["label"] # 标签列
return data,label
# 定义sigmod函数
def sigmod(x):
return 1.0 /(1 + np.exp(-x))
# 返回权重函数
def gradAscent(data,label):
m,n = data.shape # m(行数)=100,n(列数)=3(特征数)
data = np.mat(data) # 将数据转化为矩阵 100*3
label = np.mat(label).T # 将标签转化为矩阵 100*1
weights = np.ones((n,1)) # 初始化回归系数,每个系数初始化为 1.0,三行一列
maxCricles = 5000 # 迭代次数
alpha = 0.001 # 步长(学习率)
for i in range(maxCricles):
h =sigmod(data*weights) # 将数据的特征值*系数的值作为 sigmod函数的输入
error = label - h # 计算每个样本的sigmod函数输出与标签的差值
weights = weights + alpha*data.T*error # 更新权重
#print("第 {} 次循环,error[0]= {}".format(i + 1, error[0]))
return weights
# 画出最终分类的图
def plotBestFit(data,label,weights):
data = np.array(data) # 将数据转化为数组
weights = np.array(weights) # 将权重转化为数组
m = data.shape[0] # 数据的条数m
x0 = []; y0 = []; # 标签为0的数据点的x坐标,y坐标
x1 = []; y1 = []; # 标签为1的数据点的x坐标,y坐标
for i in range(m):
if label[i] == 0:
x0.append(data[i,1]); y0.append(data[i,2])
else:
x1.append(data[i,1]); y1.append(data[i,2])
plt.scatter(x0,y0,c="red",marker="s")
plt.scatter(x1,y1,c="green")
x = np.arange(-3.0,3.0,0.1) # 直线的x坐标
y = (-weights[0] - weights[1]*x)/weights[2] # 直线的y坐标
plt.plot(x,y)
plt.xlabel("x1")
plt.ylabel("x2")
plt.show()
# 定义主函数
def main():
weights = gradAscent(data,label)
print("权重:\n",weights)
plotBestFit(data,label,weights)
main()
结果截图:
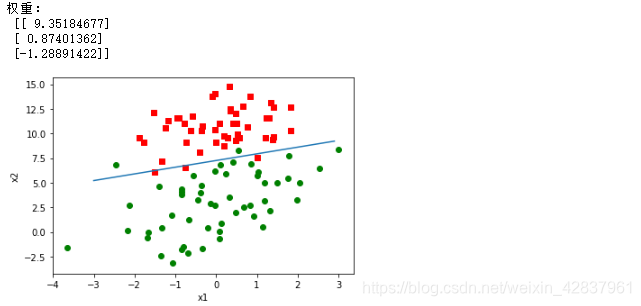
下面的代码是用 python 直接写好的逻辑回归函数:以后直接使用。
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
# 1.读取数据
data = pd.read_csv("data.csv")
print(data.head())
print("shape:",data.shape)
# 2.建立逻辑回归模型
#(1)构建 X(特征向量)和 y(标签列)
feature_cols = ["x1","x2"]
X = data[feature_cols]
y = data["label"]
#(2)构建训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X,y,random_state=1) # 25% 测试
#(3)构建逻辑回归模型并训练
model = LogisticRegression().fit(X_train,y_train)
#(4)输出模型结果
print("截距:",model.intercept_)
print("回归系数:",model.coef_)
# 3.预测
y_pred = model.predict([[0.5564,-1.5543]])
print("预测类别:",y_pred)
# 4.评价模型准确率
model.score(X_test,y_test)
运行结果截图:
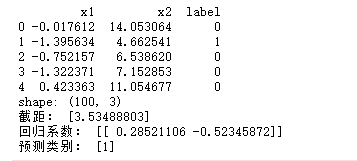
更多推荐
 已为社区贡献5条内容
已为社区贡献5条内容








所有评论(0)