【C++】求两个数的最大公约数——方法大全
最大公约数定义如下:
公约数,也被称为“公因数”。它是一个能被若干个整数同时均整除的整数。如果一个整数同时是几个整数的约数,称这个整数为它们的“公约数”,公约数中最大的整数即为“最大公约数”。
以下我将介绍8种求最大公约数的方法,这些方法中,最常用到的公约数求法的思想我已用代码实现了,并附有运行结果的分析,小伙伴看完就再也不用怕最大公约数和最小公倍数的题了!!
主要算法及示例
题目:输入任意两个数n,m,求它们的最大公约数。
1. 查找公约数法
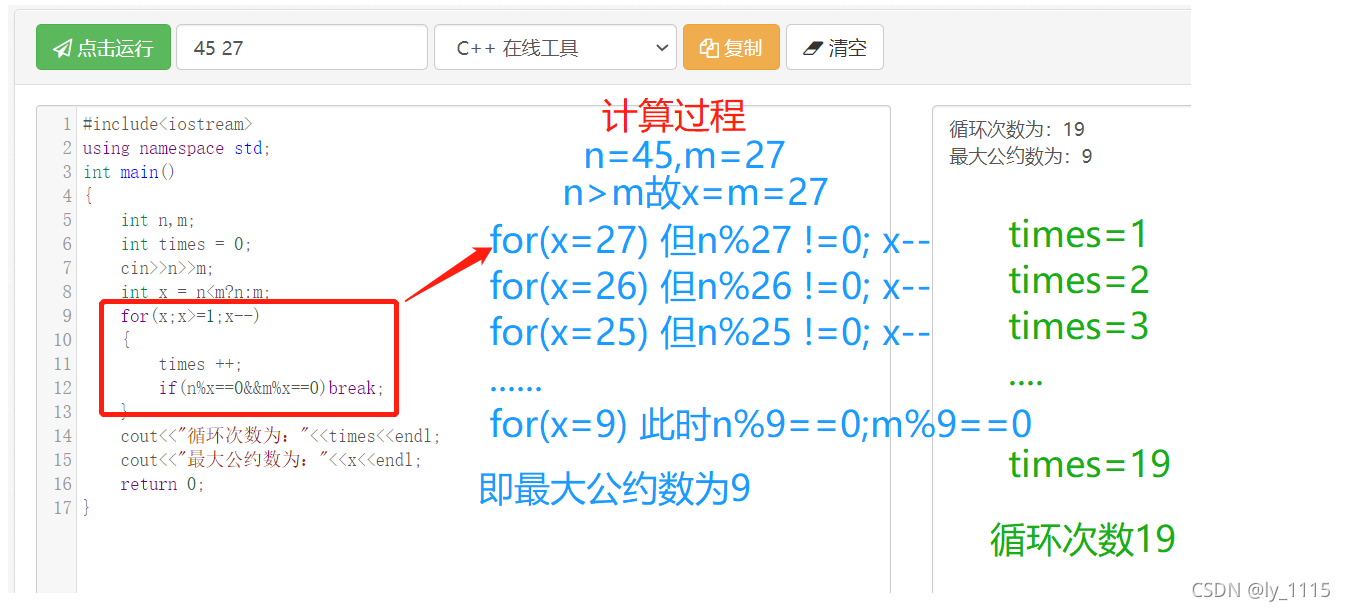
根据已有的数学知识我们知道,m>n的话,m,n的最大公约数永远不可能是m(因为n/m不能整除),只可能是n。所以我们只需要从n开始依次向较小数找到“能同时被n,m整除的第一个整数”即为两数的最大公约数。代码实现如下:
#include<iostream>
using namespace std;
int main()
{
int n,m;
int times = 0;
cin>>n>>m; //输入两个数
int x = n<m?n:m; //m,n的最大的公约数永远不可能是较大的那个数,只可能是较小的数
for(x;x>=1;x--)
{
times ++;
if(n%x==0&&m%x==0) //x正好被n,m整除,则找到了x
break;
}
cout<<"循环次数为:"<<times<<endl;
cout<<"最大公约数为:"<<x<<endl;
return 0;
}
运行结果分析:

2. 更相减损法
1)判断两个数是否是偶数,如果是就用2约简至两个数都不是偶数;如果不是则执行第二步
2)假设a>b,则c = a-b,接着c与b比较,再次较大的数减去较小的数,直到较小的数与当前的差c相等。
则最大公约数等于第一步中约掉的若干个2与第二步中得出的c的乘积。
#include<iostream>
#include <math.h>
using namespace std;
int main()
{
int n,m;
cin>>n>>m;
int times = 0; //循环次数
int count = 0; //2被除的次数
int result = 0; //结果
while(m%2 == 0 & n%2 == 0){
times ++;
count++; //约掉2的次数
m /= 2;
n /= 2;
}
while(n!=m){ //更相减损
times ++;
if(n>m)n=n-m;
else m=m-n;
}
result = m * pow(2,count); //pow为math中方法
cout<<"循环次数为:"<<times<<endl;
cout<<"最大公约数为:"<<result<<endl;
return 0;
}
运行结果分析:

3. 求差判定法
如果两个数相差不大,可以用大数减去小数,所得的差与小数的最大公约数就是原来两个数的最大公约数。
例如:求78和60的最大公约数用 78-60=18,18和60的最大公约数是6,所以78和60的最大公约数是6。
如果两个数相差较大,可以用大数减去小数的若干倍,一直减到差比小数小为止,差和小数的最大公约数就是原来两数的最大公约数。
例如:求92和16的最大公约数用 92-16=76,76- 16=60, 60-16=44,44-16=28,28-16=12,12和16的最大公约数是4,所以92和16的最大公约数就是4。
4. 分解因式法
先分别把两个数分解质因数,再找出它们全部公有的质因数,然后把这些公有质因数相乘,得到的积就是这两个数的最大公约数。
例如:求125和300的最大公约数,因为125= 5x5x5, 300=2x2x3x5x5,所以125和300的最大公约数是5x5=25。
5. 短除法
为了简便,将两个数的分解过程用同一个短除法来表示,那么最大公约数就是所有除数的乘积。
例如:求180和324的最大公约数,如下计算,因为9和5互质,所以180和324的最大公约数是2x2x9=36。

6. 除法
当两个数中较小的数是质数时,可采用除法求解,即用较大的数除以较小的数,如果能够整除,则较小的数是这两个数的最大公约数。
例如:求19和152的最大公约数。因为152/19=8(19是质数),所以19和152的最大公约数是19。
7. 缩倍法
如果两个数没有之间没有倍数关系,可以把较小的数依次除以2、3、…直到求得的商是较大数的约数为止,这时的商就是两个数的最大公约数。
例如:求30和24的最大公约数,24/2=12,12不是30约数;24/3=8,8不是30约数;24/4=6, 6是30的约数,所以30和24的最大公约数是6。
8. 辗转相除法

代码实现:
#include<iostream>
using namespace std;
int main()
{
int n,m;
cin>>n>>m;
int a=1; //默认在最大公约数为1
int times =0;
if(n%m==0||m%n==0) //若nm直接能整除,则最大公约数即是较小那个的数
{
times++;
m=m<n?m:n;
}
while((a=n%m)!=0)
{
times++;
n=m;
m=a;
}
cout<<"循环次数为:"<<times<<endl;
cout<<"最大公约数为:"<<m<<endl;
return 0;
}
运行结果分析:

以上就是我了解到的所有方法,之前作者用C语言也实现过 求最大公约数,有问题欢迎留言讨论~
看完记得关注博主哟~ 下篇博客是牛客网的题目:求最小公倍数!
更多推荐
 已为社区贡献5条内容
已为社区贡献5条内容







所有评论(0)