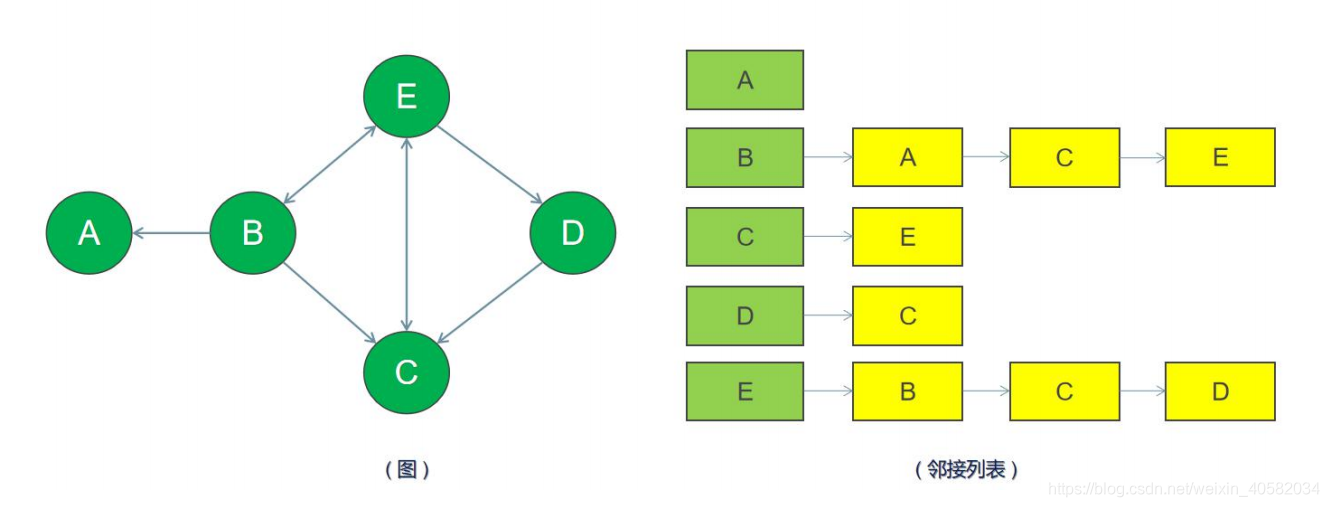
在邻接列表实现中，每一个顶点会存储一个从它这里开始的相邻边的列表。比如，如果顶点 B 有一条边到 A、C 和 E，那么 A 的列表中会有 3 条边。

bool Init(AdjListGraph &gh)
{
	gh.adjList = new VertexNode[MAXSIZE];//分配顶点数组地址
	if (!gh.adjList) return false;

	gh.numEdg = 0;
	gh.numVex = 0;

}

 邻接表的创建

//寻找顶点的数据找到数组的下标
int Location(AdjListGraph gh, char c)
{
	if (gh.numVex <= 0) return -1;

	for (int i=0;i<gh.numVex;i++)
	{
		if (c==gh.adjList[i].data)
		{
			return i;
		}
	}
	
	return-1;
}

//图的创建
void CreateALGraph(AdjListGraph &gh)
{
	cout << "输入图的定点数 和边数：";
	cin >> gh.numVex >> gh.numEdg;
	if (gh.numVex > MAXSIZE) return;

	cout << endl << "输入相关顶点： " << endl;
	//保存顶点
	for (int i=0;i<gh.numVex;i++)
	{
		cin >> gh.adjList[i].data;
		gh.adjList[i].first = NULL;
	}

	char vi, vj;//保存输入的顶点；
	int i, j;
	cout << "请依次输入边(vi,vj)上的顶点序号：" << endl;
 
    for(int k = 0; k < gh.numEdg; k++)
	{
		cin >> vi >> vj;
		i = Location(gh, vi);
		j = Location(gh, vj);

		if (i>=0 && j>=0)
		{   
            //头插法插入边
			EdgeNode *temp = new EdgeNode;
			temp->adjvex = j;
			temp->next = gh.adjList[i].first;
			gh.adjList[i].first = temp;
		}
	}
}

邻接表的深度遍历

1）深度优先遍历算法原理

1. 首先从一个未走到过的顶点作为起始顶点，比如 A 顶点作为起点。

2. 沿 A 顶点的边去尝试访问其它未走到过的顶点，首先发现 E 号顶点还没有走到过，于是访问 E 顶点。

3. 再以 E 顶点作为出发点继续尝试访问其它未走到过的顶点，接下来访问 D 顶点。

4. 再尝试以 D 顶点作为出发点继续尝试访问其它未走到过的顶点。

5. 但是，此时沿 D 顶点的边，已经不能访问到其它未走到过的顶点，接下来返回到 E 顶点。

6. 返回到 E 顶点后，发现沿 E 顶点的边也不能再访问到其它未走到过的顶点。此时又回到顶点 A（ D-> E-> A），再以 A 顶点作为出发点继续访问其它未走到过的顶点，于是接下来访问 C 点。

7. 以此类推

8. 最终访问的结果是 A -> E -> D -> C -> B

邻接表的广度遍历

1）广度优先遍历算法原理

2）广度优先遍历算法实现

//对图上的顶点进行广度遍历
void BFS(AdjListGraph &gh,int i)
{
	int cur = -1;
	queue<int> q;
	q.push(i);
	while (!q.empty())//队列不为空
	{
		cur = q.front();//取队列的头元素
		if (visited[cur]==false)
		{
			cout << gh.adjList[cur].data << " ";
			visited[cur] = true;
		
		}
		q.pop();
		//取当前结点相邻的结点入队
		EdgeNode *tmp = gh.adjList[cur].first;
		while (tmp!=NULL)
		{
			q.push(tmp->adjvex);
			tmp = tmp->next;
		}
	}
}
//对所有顶点进行广度遍历
void BFS_All(AdjListGraph &gh)
{
	for (int i = 0; i < gh.numVex; i++)
	{
		if (visited[i] == false)
		{
			BFS(gh, i);
		}
	}
}

算法验证

程序清单

//Author：See qq3492625357
//代码为本人手写，若有错误或不当之处，欢迎指正。
#include <iostream>
#include <queue>
#define MAXSIZE 1024
using namespace std;

typedef struct _EdgeNode//与结点连接的边 
{
	int adjvex;//邻接的顶点 
	int weight;//权重
	struct _EdgeNode *next;//指向下一个顶点/边
}EdgeNode;

typedef struct _VertexNode//顶点结点
{
	char data;//结点数据
	struct _EdgeNode *first;
}VertexNode,*AdjList;

typedef struct _AdJListGraph
{
	AdjList adjList;//顶点数组
	int numVex;
	int numEdg;
}AdjListGraph;

//图的初始化
bool Init(AdjListGraph &gh)
{
	gh.adjList = new VertexNode[MAXSIZE];//分配顶点数组地址
	if (!gh.adjList) return false;

	gh.numEdg = 0;
	gh.numVex = 0;

}

//寻找顶点的数据找到数组的下标
int Location(AdjListGraph gh, char c)
{
	if (gh.numVex <= 0) return -1;

	for (int i=0;i<gh.numVex;i++)
	{
		if (c==gh.adjList[i].data)
		{
			return i;
		}
	}
	
	return-1;
}

//图的创建
void CreateALGraph(AdjListGraph &gh)
{
	cout << "输入图的定点数 和边数：";
	cin >> gh.numVex >> gh.numEdg;
	if (gh.numVex > MAXSIZE) return;

	cout << endl << "输入相关顶点： " << endl;
	//保存顶点
	for (int i=0;i<gh.numVex;i++)
	{
		cin >> gh.adjList[i].data;
		gh.adjList[i].first = NULL;
	}

	char vi, vj;//保存输入的顶点；
	int i, j;
	cout << "请依次输入边(vi,vj)上的顶点序号：" << endl;

    for(int k = 0; k < gh.numEdg; k++)
	{
		cin >> vi >> vj;
		i = Location(gh, vi);
		j = Location(gh, vj);

		if (i>=0 && j>=0)
		{
			EdgeNode *temp = new EdgeNode;
			temp->adjvex = j;
			temp->next = gh.adjList[i].first;
			gh.adjList[i].first = temp;
		}
	}
}

bool visited[MAXSIZE] = {0};//全局数据用来判断元素是否被访问过

//对图上的顶点进行深度遍历
void DFS(AdjListGraph &gh,int i)
{
	int nextNum = -1;
	if (visited[i])//如果该结点已经被访问则返回 
		return;

	//访问该结点
	cout << gh.adjList[i].data << " ";
	visited[i] = true;

	EdgeNode *tmp = gh.adjList[i].first;
    while (tmp)
	{
		nextNum = tmp->adjvex;
		if (visited[nextNum]==false)
		{
			DFS(gh, nextNum);
		}
	    tmp = tmp->next;
	}
	
}

//对所有顶点进行深度遍历
void DFS_All(AdjListGraph &gh)
{
	for (int i=0;i<gh.numVex;i++)
	{
		if (visited[i]==false)
		{
			DFS(gh, i);
		}
	}
}

//对图上的顶点进行广度遍历
void BFS(AdjListGraph &gh,int i)
{
	int cur = -1;
	queue<int> q;
	q.push(i);
	while (!q.empty())//队列不为空
	{
		cur = q.front();//取队列的头元素
		if (visited[cur]==false)
		{
			cout << gh.adjList[cur].data << " ";
			visited[cur] = true;
		
		}
		q.pop();
		//取当前结点相邻的结点入队
		EdgeNode *tmp = gh.adjList[cur].first;
		while (tmp!=NULL)
		{
			q.push(tmp->adjvex);
			tmp = tmp->next;
		}
	}
}
//对所有顶点进行广度遍历
void BFS_All(AdjListGraph &gh)
{
	for (int i = 0; i < gh.numVex; i++)
	{
		if (visited[i] == false)
		{
			BFS(gh, i);
		}
	}
}
int main()
{
	
	AdjListGraph G;
	cout << "正在创建邻接表，请按提示进行输入..." << endl;
    Init(G);
	CreateALGraph(G);

	cout << "正在进行深度优先遍历，遍历结果如下:" << endl;
	

	//深度优先遍历
	DFS_All(G);
	cout << endl;

	memset(visited, 0, sizeof(visited));

	cout << "正在进行广度优先遍历，遍历结果如下:" << endl;
	//广度优先遍历
	BFS_All(G);

	cout << endl;
}