
支持向量机(SVM)的回归拟合(matlab实现)
SMO算法可以看做是Osuna算法的一个特例,即将工作样本集B的规模固定为2,每次只求解两个训练样本的QP问题,其最优解可以直接采用解析方法获得,而无需采用反复迭代的数值解法,这在很大程度上提高了算法的求解速度。在求解时,先计算工作样本集B的QP问题,然后采取一些替换策略,用非工作样本集N中的样本替换工作样本集B中的一些样本,同时保证工作样本集B的规模不变,并重新进行求解。然而,目前尚存在一些亟待
一键AI生成摘要,助你高效阅读
问答
·
与传统的神经网络相比,SVM具有以下几个优点:
(1)SVM是专门针对小样本问题而提出的,可以在有限样本的情况下获得最优解。
(2)SVM算法最终将转化为一个二次规划问题,从理论上讲可以得到全局最优解,从而解决了传统神经网络无法避免局部最优的问题。
(3)SVM的拓扑结构由支持向量决定,避免了传统神经网络需要反复试凑确定网络结构的问题。
(4)SVM利用非线性变换将原始变量映射到高维特征空间,在高维特征空间中构造线性分类函数,这既保证了模型具有良好的泛化能力,又解决了“维数灾难”问题。
同时,SVM不仅可以解决分类、模式识别等问题,还可以解决回归、拟合等问题。因此,其在各个领域中都得到了非常广泛的应用。
本章将详细介绍SVM回归拟合的基本思想和原理,并以实例的形式阐述其在混凝土抗压强度预测中的应用。
1 理论基础
1.1 SVR基本思想
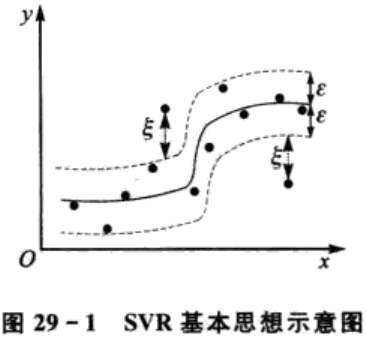
为了利用SVM解决回归拟合方面的问题,Vapnik等人在SVM分类的基础上引入了ε不敏感损失函数,从而得到了回归型支持向量机(support vector machine for regression, SVR),且取得了很好的性能和效果。下面将详细阐述SVR的基本思想并进行算法推导。 SVM应用于回归拟合分析时,其基本思想不再是寻找一个最优分类面使得两类样本分开,而是寻找一个最优分类面使得所有训练样本离该最优分类面的误差最小,如图29-1所示。




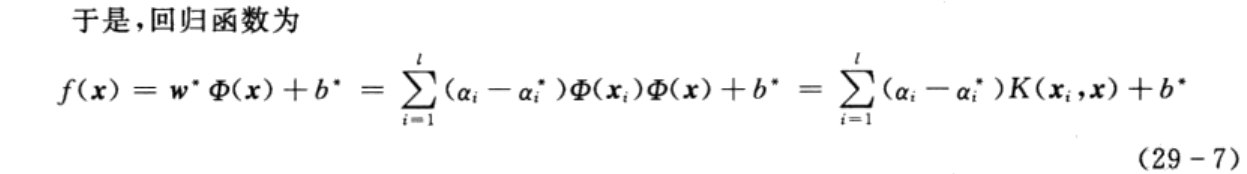
其中,只有部分参数(ai-ai*)不为零,其对应的样本xi即为问题中的支持向量。
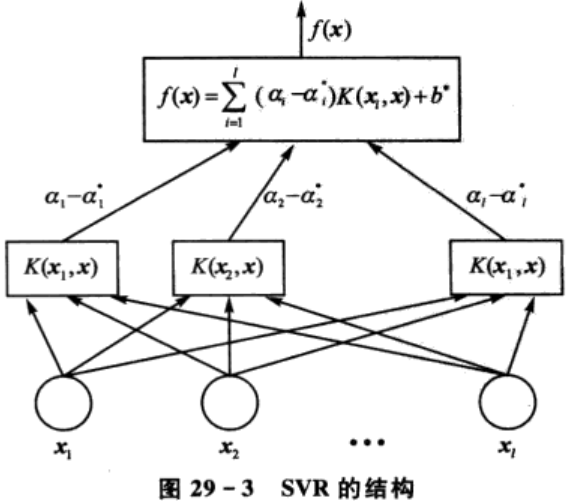
从式(29-7)可以看出,SVR最终的函数形式与SVM相同,其结构与神经网络的结构较为类似,如图29-3所示。输出是中间节点的线性组合,每个中间节点对应一个支持向量。
1.2 支持向量机的训练算法
支持向量机的求解问题最终将转化为一个带约束的二次规划(quadratic programming,

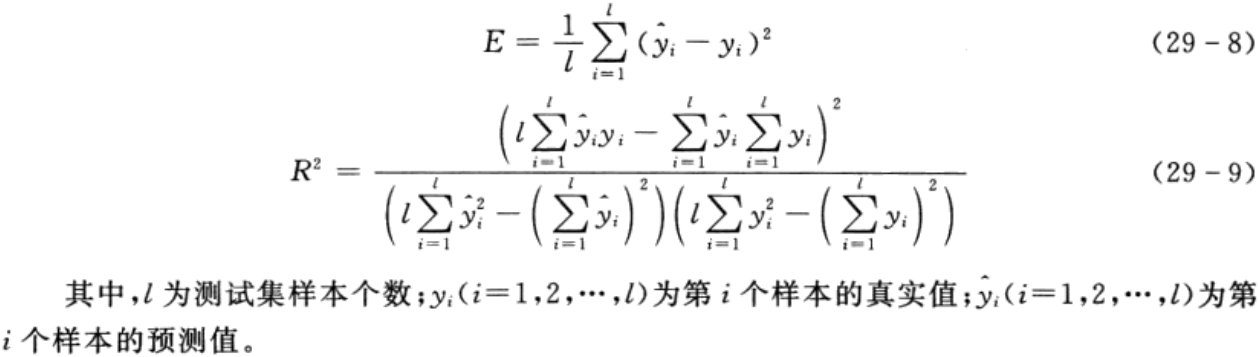

QP) 问题,当训练样本较少时,可以利用传统的牛顿法、共轭梯度法、内点法等进行求解。然而,当训练样本数目较大时,传统算法的复杂度会急剧增加,且会占用大量的内存资源。因此,为了减小算法的复杂度,提升算法的效率,不少专家和学者提出了许多解决大规模训练样本的支持向量机训练算法,下面简要介绍几种常用的典型训练算法。
1.分块算法
分块算法(chunking)的理论依据是支持向量机的最优解只与支持向量有关,而与非支持向量无关。该算法的基本步骤如下:
(1)将原始优化问题分解为一系列规模较小的QP子集,首先随机选择一个QP子集,利用其中的训练样本进行训练,剔除其中的非支持向量,保留支持向量。
(2)将提取出的支持向量加入另一个QP子集中,并对新的QP子集进行求解,同时提取出其中的支持向量。
(3)逐步求解,直至所有的QP子集计算完毕。
2.Osuna算法
Osuna算法最先是由Osuna等人提出的,其基本思路是将训练样本划分为工作样本集B和非工作样本集N,迭代过程中保持工作样本集B的规模固定。在求解时,先计算工作样本集B的QP问题,然后采取一些替换策略,用非工作样本集N中的样本替换工作样本集B中的一些样本,同时保证工作样本集B的规模不变,并重新进行求解。如此循环,直到满足一定的终止条件。
3.序列最小优化算法
与分块算法和Osuna算法相同,序列最小优化算法(sequential minimal optimization,SMO)的基本思想也是把一个大规模的QP问题分解为一系列小规模的QP子集优化问题。SMO算法可以看做是Osuna算法的一个特例,即将工作样本集B的规模固定为2,每次只求解两个训练样本的QP问题,其最优解可以直接采用解析方法获得,而无需采用反复迭代的数值解法,这在很大程度上提高了算法的求解速度。
4.增量学习算法
上述3种训练算法的实现均是离线完成的,若训练样本是在线实时采集的,则需要用到增量学习算法(incremental learning)。增量学习算法将训练样本逐个加入进来,训练时只对与新加入的训练样本有关的部分结果进行修改和调整,而保持其他部分的结果不变。其最大的特点是可以在线实时地对训练样本进行学习,从而获得动态的模型。
简而言之,分块算法可以减小算法占用的系统内存,然而当训练样本的规模很大时,其算法复杂度仍然较大。Osuna算法的关键在于如何划分工作样本集与非工作样本集、如何确定工作样本集的大小、如何选择替换策略以及如何设定迭代终止条件等。SMO算法采用解析的方法对QP问题进行求解,从而避免了数值解法的反复迭代过程以及由数值解法引起的误差积累问题,这大大提高了求解的速度和精度。同时,SMO算法占用的内存资源与训练样本的规模呈线性增长,因此其占用的系统内存亦较小。增量学习算法适用于在线实时训练学习。
2 案例背景
2.1 问题描述
近年来,随着房屋建筑、水利、交通等土木工程的大力发展,我国的混凝土年用量逐年攀升。相关统计数据表明,目前我国的混凝土年用量约为24~30亿立方米,混凝土结构约占全部工程结构的90%上,可以预见,混凝土将是现阶段及未来一段时间内我国主导的工程结构材料。
混凝土是由水泥、砂、石、飞灰和水等构成的混合物,且在使用时往往需要添加增塑剂等。 因此,与其他结构材料相比,混凝土具有更复杂的力学性能。混凝土的强度是决定混凝土结构和性能的关键因素,也是评价混凝土结构和性能的重要指标。其中,混凝土的立方米抗压强度是其各种性能指标的综合反映,与混凝土轴心抗拉强度、轴心抗压强度、弯曲抗压强度、疲劳强度等有良好的相关性,因此混凝土的立方米抗压强度是评价混凝土强度的最基本指标。
随着技术的不断发展,混凝土抗压强度检测手段也愈来愈多,基本上可以分为局部破损法和非破损法两类,其中局部破损法主要是钻芯法,非破损法主要包括回弹法和超声法。工程上常采用钻芯法、修正回弹法,并结合《回弹法检测混凝土抗压强度技术规程》、《建筑结构检测技术标准》等规定的方法来推定混凝土的抗压强度。按照传统的方法,通常需要先对混凝土试件进行28天标准养护,然后再进行测试。若能够提前预测出混凝土的28天抗压强度,则对于提高施工质量和进度都具有重要的参考意义和实用价值。
此外,不少专家和学者将投影寻踪回归、神经网络、灰色理论等方法引入混凝土结构工程领域,取得了不错的效果,对混凝土抗压强度的预测有着一定的指导意义。相关研究成果表明,混凝土的28天立方米抗压强度与混凝土的组成有很大的关系,即与每立方米混凝土中水泥、炉石、飞灰、水、超增塑剂、碎石及砂用量的多少有显著的关系。现采集到103组混凝土样本的立方米抗压强度及其中上述7种成分的含量大小,要求利用支持向量机建立混凝土的28天立方米抗压强度与其组成间的回归数学模型,并对模型的性能进行评价。
2.2 解题思路及步骤
依据问题描述中的要求,实现支持向量机回归模型的建立及性能评价,大体上可以分为以下几个步骤,如图29-4所示。

1.产生训练集/测试集
与SVM分类中类似,为了满足libsvm软件包相关函数调用格式的要求,产生的训练集和测试集应进行相应的转换。训练集样本的数量及代表性要求与其他方法相同,此处不再赘述。
2.创建/训练SVR回归模型
利用libsvm软件包中的函数svmtrain可以实现SVR回归模型的创建和训练,区别是其中的相关参数设置有所不同。同时,考虑到归一化、核函数的类型、参数的取值对回归模型的性能影响较大,因此,需要在设计时综合衡量,具体参见第3节及第4节,此处不再赘述。
3.仿真测试
利用libsvm软件包中的函数svmpredict可以实现SVR回归模型的仿真测试,返回的第1个参数为对应的预测值,第2个参数中记录了测试集的均方误差E和决定系数R2,具体的计算公式分别如下:
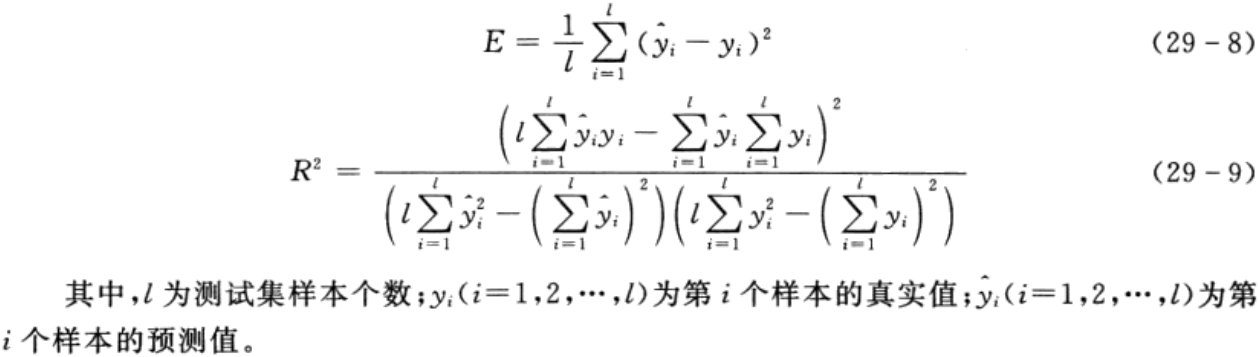
4.性能评价
利用函数svmpredict返回的均方误差E和决定系数R2,可以对所建立的SVR回归模型的性能进行评价。若性能没有达到要求,则可以通过修改模型参数、核函数类型等方法重新建立回归模型,直到满足要求为止。
3 MATLAB程序实现
利用MATLAB及libsvm软件包中提供的函数,可以方便地在MATLAB环境下实现上述步骤。
%% 清空环境变量
clear all
clc
%% 导入数据
load concrete_data.mat
% 随机产生训练集和测试集
n = randperm(size(attributes,2));
% 训练集——80个样本
p_train = attributes(:,n(1:80))';
t_train = strength(:,n(1:80))';
% 测试集——23个样本
p_test = attributes(:,n(81:end))';
t_test = strength(:,n(81:end))';
%% 数据归一化
% 训练集
[pn_train,inputps] = mapminmax(p_train');
pn_train = pn_train';
pn_test = mapminmax('apply',p_test',inputps);
pn_test = pn_test';
% 测试集
[tn_train,outputps] = mapminmax(t_train');
tn_train = tn_train';
tn_test = mapminmax('apply',t_test',outputps);
tn_test = tn_test';
%% SVM模型创建/训练
% 寻找最佳c参数/g参数
[c,g] = meshgrid(-10:0.5:10,-10:0.5:10);
[m,n] = size(c);
cg = zeros(m,n);
eps = 10^(-4);
v = 5;
bestc = 0;
bestg = 0;
error = Inf;
for i = 1:m
for j = 1:n
cmd = ['-v ',num2str(v),' -t 2',' -c ',num2str(2^c(i,j)),' -g ',num2str(2^g(i,j) ),' -s 3 -p 0.1'];
cg(i,j) = svmtrain(tn_train,pn_train,cmd);
if cg(i,j) < error
error = cg(i,j);
bestc = 2^c(i,j);
bestg = 2^g(i,j);
end
if abs(cg(i,j) - error) <= eps && bestc > 2^c(i,j)
error = cg(i,j);
bestc = 2^c(i,j);
bestg = 2^g(i,j);
end
end
end
% 创建/训练SVM
cmd = [' -t 2',' -c ',num2str(bestc),' -g ',num2str(bestg),' -s 3 -p 0.01'];
model = svmtrain(tn_train,pn_train,cmd);
%% SVM仿真预测
[Predict_1,error_1] = svmpredict(tn_train,pn_train,model);
[Predict_2,error_2] = svmpredict(tn_test,pn_test,model);
% 反归一化
predict_1 = mapminmax('reverse',Predict_1,outputps);
predict_2 = mapminmax('reverse',Predict_2,outputps);
% 结果对比
result_1 = [t_train predict_1];
result_2 = [t_test predict_2];
%% 绘图
figure(1)
plot(1:length(t_train),t_train,'r-*',1:length(t_train),predict_1,'b:o')
grid on
legend('真实值','预测值')
xlabel('样本编号')
ylabel('耐压强度')
string_1 = {'训练集预测结果对比';
['mse = ' num2str(error_1(2)) ' R^2 = ' num2str(error_1(3))]};
title(string_1)
figure(2)
plot(1:length(t_test),t_test,'r-*',1:length(t_test),predict_2,'b:o')
grid on
legend('真实值','预测值')
xlabel('样本编号')
ylabel('耐压强度')
string_2 = {'测试集预测结果对比';
['mse = ' num2str(error_2(2)) ' R^2 = ' num2str(error_2(3))]};
title(string_2)
%% BP 神经网络
% 数据转置
pn_train = pn_train';
tn_train = tn_train';
pn_test = pn_test';
tn_test = tn_test';
% 创建BP神经网络
net = newff(pn_train,tn_train,10);
% 设置训练参数
net.trainParam.epcohs = 1000;
net.trainParam.goal = 1e-3;
net.trainParam.show = 10;
net.trainParam.lr = 0.1;
% 训练网络
net = train(net,pn_train,tn_train);
% 仿真测试
tn_sim = sim(net,pn_test);
% 均方误差
E = mse(tn_sim - tn_test);
% 决定系数
N = size(t_test,1);
R2=(N*sum(tn_sim.*tn_test)-sum(tn_sim)*sum(tn_test))^2/((N*sum((tn_sim).^2)-(sum(tn_sim))^2)*(N*sum((tn_test).^2)-(sum(tn_test))^2));
% 反归一化
t_sim = mapminmax('reverse',tn_sim,outputps);
% 绘图
figure(3)
plot(1:length(t_test),t_test,'r-*',1:length(t_test),t_sim,'b:o')
grid on
legend('真实值','预测值')
xlabel('样本编号')
ylabel('耐压强度')
string_3 = {'测试集预测结果对比(BP神经网络)';
['mse = ' num2str(E) ' R^2 = ' num2str(R2)]};
title(string_3)
4 延伸阅读
4.1 核函数对模型性能的影响
为了衡量不同核函数类型对模型性能的影响,这里以某次随机产生的训练集和测试集进行对比试验,具体结果如表29-1所列。

从表中可以清晰地看到,RBF核函数对应的模型泛化能力最好,与线性及Sigmoid核函数相比,尽管多项式核函数对应的模型训练集性能较好,但其泛化能力较差。
支持向量机不仅可以应用在分类、模式识别问题中,亦可以应用于回归拟合中。近年来,随着研究的深入,支持向量机以其良好的性能在各个领域都得到了广泛的应用。然而,目前尚存在一些亟待解决的问题,也是研究的热点问题,如探索适合于处理大规模问题的算法、在线实时学习、移植于硬件平台中等。
更多推荐
 已为社区贡献23条内容
已为社区贡献23条内容










所有评论(0)