从零开始之电机FOC控制
我们将撕开FOC神秘而虚伪的面纱,以说人话的方式讲述它。真正的做到从零开始,小白一看就会,一学就废。
如果觉得有用的话,就点个赞呗,纯手码。
一、什么是FOC?
FOC是Field Orientation Control的缩写,字面意思是场方向控制,在电机应用场景下就是磁场方向控制。
现在问题来了,挖掘技术哪家强?不是,走错了再来,那么问题来了,就不能像小时候四驱赛车马达一样,通个电直接就转了,不简单粗暴多了,为啥电机控制就要用到FOC呢?这个问题得问你啊,你不用它不就没有那么多屁事了。
二、学习门槛
FOC是关于电机的一种驱动方式,由于这个东西过于高深,不建议啥都不懂的小伙伴学习,所以要了解并使用它,得具有以下理论基础:
- 初中物理,部分电磁学,需要明白如何由电生磁。
- 高中物理,力的分解与合成。
- 高中数学,向量运算,向量=矢量;三角函数。
- 电路、程序基础,这个就不用多说了,懂的都懂。
三、电机构成
电机分类大概如下所示。

一般的移动或小型的应用场景因为电源是电池类型为低压直流,所以较为常见的为直流电机。
3.1 有刷电机
有刷电机,也就是四驱车马达电机那种,内部结构如下图所示。

正常情况下,要让电机转动很简单,用手拨就可以让电机转动,现在都什么时代了,还要自己动手?那有什么能够代替我的手呢,就是用另外一种力替代我手拨动的这个力就行了,万有引力行不行呢,不行,虽然说两个物体相互吸引,但是这个力太小了,而且不能控制大小,所以我需要一种力气大小可控的力。
磁铁大家应该都玩过,磁场越强的磁铁吸到一起后就越难分开。根据电磁学第二定律,通电电流约大,磁场越强,那么磁力也就越大,那这力气不就来了嘛。
有了力气,那么我就用上去呗,我们定义上面能转动的磁铁叫做转子,下面固定不动的磁铁叫做定子,用了之后发现,也只能动一下,要让它连续转动,好像还要合计合计。如果当要达到稳定状态时,改变定子的磁极,这时候会产生一个排斥力,让它继续转动,只要我在合适的时间变换定子的磁极,那转子不就一直在转动。
用手动变化定子磁极的话太累了,根据初中物理的安培定则即右手螺旋定则,线圈+电流=磁铁,而且方向可控,同时磁力大小与电流成正比。PS:电磁学三大定律:法拉第电磁感应定律、安培环路定理、麦克斯韦-安培定律,描述了电场和磁场之间的相互作用关系。


于是乎有了下面的状态,

当要达到稳定状态时,改变一下电流方向,线圈磁极也跟着改变后,就会产生一个继续波动的力,如下图。

有刷电机,刷子和换向器的作用,就是更换电流方向。一个线圈、一个磁极、一个刷子+换向器就能实现转动了,一台电机原型机就出来了。
为什么拆过的那些电机有好几个磁铁和线圈呢?不是一个就够了么,搞那么多不是浪费。你听我解释,我有借口,不是,我有理由这么做,多线圈和磁极的设计有以下目的和优势:1、增强转矩,可以提供更多的磁场与线圈的相互作用,进一步增强转矩。2、平滑转动,通过交替激活不同的线圈,可以使电机的输出转矩更加连续和均匀,减少震动和振动。3、改善运行特性和控制性能等。
不过话说回来,咱还没搞懂原型机怎么转动呢,你就跟我扯什么性能,我这不是话说开了就收不住,书接上回,以有刷电机的原型机为例分析原型机怎么转动的,直接花大价钱拿一个奥迪双钻梦之队经典四驱车马达来分解说明。
四驱马达车实物内部图如下所示。

根据线圈与电刷的接触程度可以分为以下四个过程,电机转动就在这四个过程之前依次不断循环。这里驱动电源始终是直流不用变化,变化的是线圈的接触改变线圈里面流过的电流,从而完成磁场的转换。





至此有刷电机的转动分析完成,而实际有三个线圈是为了规避图1的状态,避免卡死到中间不转的情况。其他电机也是从这个基础上延伸出来,俗话说的好,万丈高楼平地起,基础了解完了就可以开始深一步的学习。
3.2 无刷电机
无刷电机,常见四旋翼无人机电机,内部结构如下图所示。

无刷电机,顾名思义相比较上面的有刷电机,无刷就是没有刷子,那没有刷子的话,如何完成换向,同时这么做的优点是什么,对吧,没有好处你跟我整这么一出,那别人肯定不买账,那么听我慢慢道来。还有就是为啥是三相的?
了解一下三相电机的优点,主要原因:三相电源不是同时交替,而是同一时刻每相相差120°相位,这就意味着在任意时刻,三相提供的电压总和相同,相当于一个恒定的电源,这是单向系统不具备的。
其他优点:
- 增加带负载能力,同等条件下,三相能运输的功率是单向的三倍,因为有三根线。
- 三相电机还具有更高的功率因数,这意味着它们在给定负载和效率下消耗更少的能量。
- 相比较单向的脉冲,三相提供恒定功率,使电机运行更加稳定。
- 等等,但是也有缺点,相比较单向电机应用起来复杂等。
反正就是优胜劣汰的结果,导致这玩意就是三相结构,而你就是要了解学习它。
好了既然定下了电机构造,然后来分析一下,由上面有刷电机的了解,线圈内的电流是需要换向才能让电机转起来的。
单向有刷电机,通电就转,因为内部有电刷和换向器完成线圈电流的换向,三相无刷电机没有电刷,外部驱动用MOS管开关,完成线圈内电流的换向。
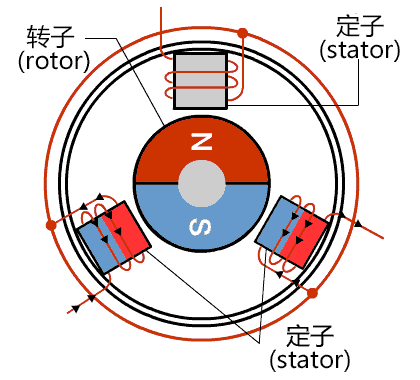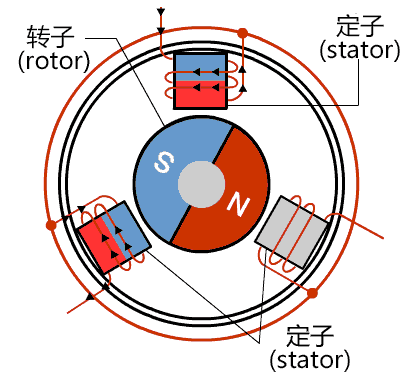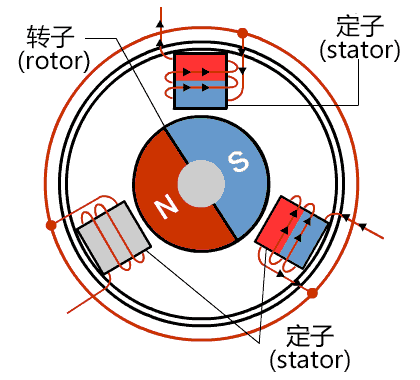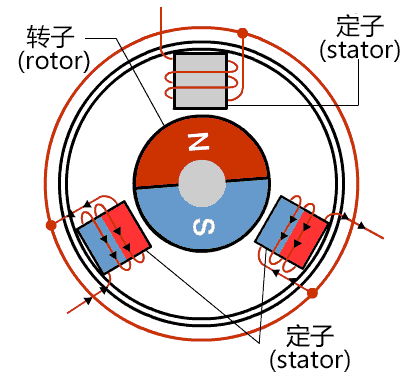
按照有刷电机的逻辑去驱动三相电机,按一定顺序依次将每一个线圈通电,这个过程称为六步换向法。三相电机线圈的控制一共有8种状态,去掉全开(111)和全关(000)两种运行过程中没用的状态,剩6种,把它分布到电机上去,如图所示。


按照顺序驱动电机就可以控制正反转了,如下图,霍尔传感器数据代表线圈状态,下表是力矩情况。

可以看出转矩一点都不平滑,有大有小,为了使电机转动更快,能源转换效率更高,就不能使用这种驱动方式。
那可能就会有人问了,有没有一种方式,可以控制磁场的大小,每时每刻都让转动方向的磁力维持最大,那么这样的情况下,能量的转换效率也越高,电机的转速就越快,是不是很妙啊。
不知道怎么做之前,先取个名字吧,不如就叫做磁场方向控制Field Orientation Control,简称FOC。
四、FOC学习
需要控制磁场力,首先要分析磁场力,然后根据想要达到的状态去控制磁场最后达到目标状态。可以分解为下面三个步骤:
- 分析磁力:目的在于要知道如何去控制它
- 采集数据和计算误差:采集到实际的数据并与设定的数据与实际数据误差
- 调节输出:将误差反馈控制输出。
4.1分析磁力:
那么如何优化这个控制呢,那么从数学和物理学的角度出发分析出解决方案,设某一时刻,磁铁和线圈的磁场如下所示。


以转子磁铁一边为原点,建立直角坐标系,这个坐标系随磁铁旋转,所以称为旋转坐标系,平行于磁铁的称为磁轴,垂直于磁铁的称为旋转轴。
将磁铁所受到的力分解到这两个坐标轴上,并命名为Q正交力,D正向力。转子在运行过程中受到这两个力的作用,在其中D不做功,没啥作用,所以要把这个力控到0,另一个力Q旋转轴上的力,用于旋转,如想要获得最大转速,那么就使转子受到的Q正交力始终保持最大,D为0,这种情况下,效率最高,转速最快。同样的道理,如果Q为0,D最大,那么电机就处于扭矩最大的静止状态。
接下来将三个线圈的力作用分析到磁铁上去,首先对线圈磁场进行分析,因为磁力的大小是不知道的,但是根据电磁学,力的大小与流过线圈的电流大小成正比,所以将电流大小等效为力的大小。又因为定子线圈相对位置固定即相互夹角为120°,电流(磁力)矢量图如下所示。

如何将这个力分析到磁铁上去呢?
下面的目的就是解答一道数学题,问题:在已知两个坐标轴:线圈磁场力坐标系和磁铁旋转坐标系,线圈磁场力坐标轴有三个磁力向量大小为Ia、Ib、Ic,互相间隔120°,两个坐标系的夹角为θ范围在0-360°,将线圈磁场力坐标系上的三个磁力向量分解导磁铁旋转坐标轴上,并求出其大小。
解:整个过程大致是将一个坐标系上的三个向量(三相磁力)变换到另一个夹角为θ的坐标系上的两个坐标轴上,这个过程用数学上称之为解耦。
答:根据参考答案可知,
步骤1:先将三个向量变成两个向量,
步骤2:根据θ,将两个向量分解到磁铁旋转坐标轴上。
最终我们将三个线圈产生的磁力转换为转子磁铁受到的Q正交力和D正向力。
人们喜欢将步骤1叫做clarke变换,步骤二叫做park变换。其实这两个变换的本质还是向量的正交分解和加减运算。
clarke变换:

由:

可得:

Park变换:


这里,因为线圈坐标系是固定的,磁铁坐标系是旋转的,磁铁坐标系与与线圈坐标系为θ,这个角度是怎么知道的呢?因为转子会装上一个位置传感器,即编码器、霍尔传感器等,用来感知转子的位置,所以这个角度是已知的。
综上,知道两个线圈的电流大小和转子位置后,就知道当前转子的受力情况,为啥不是三个线圈?因为三相线圈接法使三相电流总和为0。
4.2 采集数据和计算误差:
由上述我需要采集的数据:
- 当前线圈电流值:通过电流三个线圈的电流值,可以得到三个线圈产生的磁力。
- 转子位置状态:速度、当前角度值等,通过角度,将磁力分解到转子上,形成旋转轴的Q正交力和磁轴的D正向力。这个角度可以通过编码器或者霍尔传感器获得。速度用于后续的控制。
我需要确定的控制状态:
- 根据设定的控制状态转换为Q、D参数。
- 例如,在一定转速的情况下,尽量减小无用的D,使Q保持为定值而不是像六步换向法那样力矩有大有小,这种情况下能量转换效率最高。
- 其他控制:位置闭环、力矩闭环等。
4.3 控制:
以转速一定为例,实际速度可以通过实时采集位置数据/时间得到。再根据设定的速度与实际速度的误差去改变力矩大小,这个过程称为反馈调节,工业上常用PID算法调节误差,注:这个误差值的大小取值可能是0-最大速度的任意值。
通过误差值,按照PID算法系数,可计算出下一个控制状态的Q、D值,然后将这个Q、D施加到线圈上去改变电机运行状态,当误差为0时就达到了设定的目标状态,下面内容就是讲这方面的。
那么问题来了,已知Q、D,如何将这两个参数转换为磁场力?答案是通过控制线圈,进而控制转子磁场,最后达到控制效果。
有两个问题需要解决,1、如何控制线圈电流,从而达到控制磁场的目的。2、Q、D值如何转换为线圈电流的控制量。
首先第1点:
由电磁学可知,线圈的磁场大小与流过线圈的电流成正比,而线圈电阻一定,所以施加在线圈两端的电压大小也与线圈磁场成正比。于是乎,我改变线圈电压不就等于改变线圈电流,不就等于改变磁场,不就等于改变对转子的磁力了么。
那么问题来了,最终控制量Q、D大小任意、可正可负,目前线圈电压就两种,那么为0要么为1,这大小怎么改变呢?别急,有一种东西叫做脉宽调制,PWM(Pulse Width Modulation)。
大概意思是一个幅值为1V的方波,通过调节占空比可以将方波等效为0-1V之间的任意电压,如下图所示。

将目标控制量用PWM调制出来就可以实现控制了。
所以第1个问题答案:通过PWM控制线圈电压就可以达到控制线圈磁场的目的。
然后第二点:
这就相当于线圈磁力转换为转子受力的逆变换,将旋转坐标系下的两个向量转换为固定坐标系下的三个线圈电压向量,再通过第一点实现控制。
1、将旋转坐标系两个向量转换固定坐标系下的两个向量,这个过程需要用到park逆变换,如下图。


由向量的运算,可将转换后的固定向量转换为一个向量,那么这个向量就是以A为原点,随着转子360°旋转,如下图。

2、如何由固定的三个线圈电压向量合成上述转换后的一个向量,就是后面所说的。
我们已知三个线圈向量,有六种状态即6个向量,如下图。

那么将三个向量合成一个大小固定绕原点旋转360°的向量,大概意思如下图,改变三个向量的大小即可。




转换输出的这个过程称为PWM调制,又因为是调制结果是合成空间矢量,所以也称为空间矢量脉宽调制(Space Vector Pulse Width Modulation)。
总结:
整个过程的流量框图可以描述为下图所示:

经过上述过程就已经达到了Q、D到磁场转换的目的了,后续就是完善控制逻辑和程序算法细节。
优点
FOC:磁场控制,可以精确控制电机内部线圈的磁场强度,从而达到想要的控制效果,相比较一般控制类型,这种控制效率、精度更高,性能更强、功能更多。
效率对比:
YouTube上有个实验,在同样的条件下,用FOC控制和六步换向法控制无刷电机风机吹动小车,测量小车移动的距离来判断风机的效率。

FOC驱动风机:https://www.youtube.com/watch?v=o36Ic2RPxdA

六步换向法驱动风机:https://www.youtube.com/watch?v=Yw9mPKjb9pc

同样的条件下,FOC吹动玩具车的距离是六步换向法的6倍,六步换向法驱动风机转速为17895rpm,而FOC驱动的风机转速达到了29310rpm,快了64%。
附录一
clark变换:一种简化三相电路分析的数学变换α-β变换,由Edith Clarke于1937-1938发表了关于不平衡三相问题的修改计算方法的论文中提及。

park变换:是目前分析同步电动机运行最常用的一种坐标变换,由美国工程师派克(R.H.Park)在1929年提出。派克变换将定子的a,b,c三相电流投影到随着转子旋转的直轴(d轴),交轴(q轴)与垂直于dq平面的零轴(0轴)上去,从而实现了对定子电感矩阵的对角化,对同步电动机的运行分析起到了简化作用。

参考资料来源:
更多推荐
 已为社区贡献3条内容
已为社区贡献3条内容







所有评论(0)