首先说一下差分信号，简单来说，一个差分对就是中间带有一些耦合的一对传输线。

我们一般会在信号传输路径和返回路径之间测量单端信号，但是对于差分信号来说，我们会在差分对内的两根信号线之间进行测量。

 在上图中，V1代表着line1单线的单端电压，V2代表着line2单线的单端电压，那么差分电压就是

Vdiff=V1-V2

除了携带信息的信号之外，电路中还存在共模信号，共模信号就是两条信号线上的平均电压：

Vcommon=1/2(V1+V2)

反过来，如果已知Vdiff和Vcommon，那么：

V1=Vcomm+1/2Vdiff

V2=Vcomm-1/2Vdiff

 上图是某差分信号的差模分量和共模分量，差模分量由-0.25V到0.25V，因此，传输电压是0.5V。而共模分量一直保持1.25V。

在理想情况下，通常认为共模信号是不变的，由于不携带信息，所以共模信号不影响信号完整性。但是如果共模信号被迫改变，则会导致两个十分严重的问题：

1.如果共模信号电压过高，会使差分接收器的输入放大器饱和，不能准确读入差分信号；

2.如果在同轴线缆中有变化的共模信号，将会潜在引入过量的EMI。

差分对最重要的电气特性是差分信号看到的阻抗，我们称之为差分阻抗。(The most important electrical property of a differential pair is the impedance the differential signal sees, which we call the differential impedance.)

差分阻抗是差分信号电压与其电流的比值。先考虑没有耦合情况下差分阻抗的情况。

假设两根传输线离得够远，线距至少大于2倍的线宽，此时每根线的单端特性阻抗是Z0是50Ω，那么流经传输线和返回路径的电流为：

其中，Ione是一根信号线和返回路径之间的电流，Vone是信号线和返回路径之间的电压，Z0是信号线的单端特性阻抗。

如果第一根线上的电压跳变是0V到1V，第二根是从1V到0V，那么第一根线上的电流大小是1V/50Ω=20mA，方向是从信号线流入返回路径，第二根上的电流同样是20mA，但方向是从返回路径流向信号线。那么差分信号的阻抗是：

差分阻抗的大小是单端信号线特性阻抗的2倍，也就是100Ω。因为两根信号线之间的电压是每根信号线自身电压的2倍，而流经差分信号线的电流与单端信号线相同。

插入一点，如果差分信号传输到接收终端，终端的差分阻抗将会很大，使得差分信号反射回源端，多次反射之后就会产生振铃，解决方法就是在终端端接合适的电阻，阻值就是传输线的差分阻抗。

 

 那如果有耦合的情况呢？

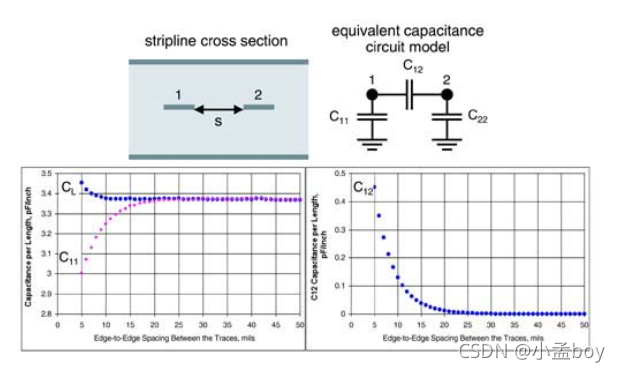
首先说一下，怎么表示耦合强度，一般是用单位长度上的互感电容C12和互感电感L12来描述。随着两根线越来越近，C11和C12都发生了变化，由于信号线1和返回路径之间的边缘场被临近的信号线阻断了，所以C11会减小，C12会增加。但是负载电容CL=C11+C12变化不大。

 上图展示了FR4板材中两个5mil线宽、50Ohm阻抗的带状线的等效电容电路，并展示了C11/C12/CL是如何变化的。

很重要的一点，由电容和电感矩阵元件描述的耦合完全独立于任何施加的电压。 它们纯粹与导体集合的几何形状和材料特性有关，就是说仅仅和走线的线宽线距和PCB板材有关。

对于电感来说，随着两根线距离越来越近，L11和L12都会改变,L11会由于相邻走线的感应涡流而略有下降，L12会上升。

 随着两根走线越来越近，耦合程度也越来越高，然而，即便是耦合最紧的情况，间距等于线宽，最大的相对耦合程度，即C12/CL,L12/L11也不会超过15%。如果线间距超过15mil，相对耦合程度小于1%，几乎可以忽略。

 在两根线离得很远的情况下，其中一根走线的特性阻抗和另一根线没有任何关系，特性阻抗和C11反向变化：

其中，Z0是走线的特性阻抗，C11是信号线和返回路径之间的电容。

当线路靠得更近时，另一条线路的存在会影响线路 1 的阻抗。这就是邻近效应（proximity effect）。如果第二条线路连接到返回路径，即，将 0-v 信号施加到线路 2，并且只有线路 1 被驱动，线路 1 的阻抗将取决于其在另一条线路附近的负载电容。 被驱动线的特性阻抗将与被驱动的单位长度电容有关：

其中Z0表示传输线的特性阻抗，C11表示信号线和返回路径之间单位长度的电容，C12表示差分线之间单位长度的电容，CL表示一条线单位长度的负载电容（loaded capacitance）

在差分走线线间距变小的过程中，走线1的阻抗会轻微降低，不超过1%，下图展示了在线间距变小的过程中，走线1的单端特性阻抗变化曲线，如果第二条线路被固定在低位并且这对走线靠得更近，则单端特性阻抗基本不变。

然而，假设第二条走线上面也有驱动，而且信号方向和line1相反，即line1上面的电压从0到1V，line2上的电压是0到-1V，当line1上的电压开始变化的时候，line1和返回路径之间的dV11/dt会在电容C11上产生一个电流，此外，line1和line2之间变化的电压dV12/dt也会产生电流，其中V12=2*V11。某一根走线上的电流可以描述为：

其中Ione表示其中一条传输线上的电流，v表示信号的传输速度，C11表示传输线和返回路径之间的电容，V11表示传输线和返回路径之间的电压，C12表示单位长度两条传输线之间的电容，V12表示两条传输线之间的电压，Vone表示其中一条线和返回路径之间的电压，RT表示传输信号的上升时间。

由于传输的信号是相反方向，因此在两条线离得越来越近的过程中，在line1上的电流会增加，以驱动更高的电容。

TIP：对于相同的供电电压，如果电流增加，那么输入阻抗会降低，如果供电电压相反，单线的特性阻抗会降低。

假设第二根传输线的驱动电压和第一根相同，那么这两根传输线之间没有相对电压，驱动端只能看到电容C11，此时其中一根传输线的电流可以表示为：

其中，Ione表示其中一条传输线上的电流，v表示信号的传输速度，C11表示传输线和返回路径之间的电容，V11表示传输线和返回路径之间的电压，C12表示单位长度两条传输线之间的电容，Vone表示其中一条线和返回路径之间的电压，RT表示传输信号的上升时间。

可以看出来，在两根线靠近的过程中，line1的单端特性阻抗并不是一个固定值，取决于line2的驱动方式，如果line2没有电压，那么line1的单端特性阻抗接近于非耦合阻抗，如果line2的电压和line1相反，则line1的阻抗会更低。如果line2的电压和line1的电压相同，那么line1的阻抗会更高。

 这是一个非常重要的观察，当处理单端信号的时候，只有一种阻抗来描述一个传输线，但是考虑到差分对并且有耦合的情况下，有三种阻抗来描述传输线。我们需要识别新的标签来描述我们谈论的三种不同阻抗中的哪一种。因此，我们将在本章后面介绍术语奇模阻抗和偶模阻抗，以提供描述差分对属性的清晰明确的语言。

TIP：当走线间距小于大约三个线宽时，相邻走线的存在将影响第一条走线的特性阻抗。 必须考虑它的接近度以及驱动它的方式。

如果一对传输线由差分信号驱动，由于耦合的原因，每条线的阻抗会降低。当差分信号沿差分对传输时，差分信号看到的阻抗将是每条线路的阻抗与其各自返回路径的串联组合。 带有耦合的差分阻抗仍将是任一线路的特性阻抗的两倍。 只是每条线路的特性阻抗由于耦合而降低。

下图显示了随着线路间距减小时的差分阻抗。 在可以实际制造的最接近的间距（即，等于线宽的间距）下，一对耦合的带状线的差分阻抗仅比带状线相隔三个线宽且未耦合时减少约 12%。