一、二叉树的性质

本期的 DFS 与 BFS 搜索算法，我将围绕二叉树来讲解，所以在了解什么是 BFS 与 DFS 之前，我们先来回顾一下二叉树 的基本概念

1.1 二叉树的特性

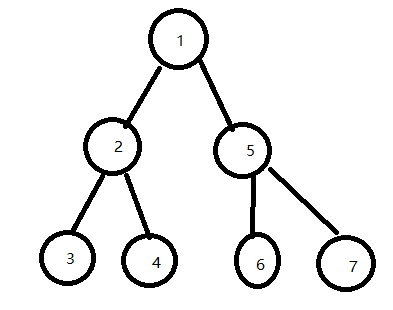
学过 数据结构与算法 的同学在接触二叉树的时候，一定遇到过 二叉树的遍历问题，因为二叉树的 本质 就是一个链表,我们可以看看一个二叉树的样子（PS：二叉树还可以使用数组来存储，当然仅限 完全二叉树）

通过上图，我们可以看出二叉树有如下特点：

1. 它有且只有一个根节点，则是权值为 1 的节点
2. 每个父节点有两个儿子节点，也可以只有一个节点
3. 每个节点的儿子数量都是两个，这样的二叉树叫做 完全二叉树
4. 每个节点的孩子可以分为 左孩子 和 右孩子

1.2 二叉树的遍历方式

在这里我们已二叉树为例，我们知道二叉树的遍历方式有如下四种，如果不理解前三种遍历，后面在 DFS 中，我会深入的讲解

1. 先序遍历（先遍历根节点，然后左节点，右节点）
   遍历结果 1 2 3 4 5 6 7
2. 中序遍历（先遍历左节点，然后根节点，然后右节点）
   遍历结果 3 2 4 1 6 5 7
3. 后续遍历（先遍历左右节点，然后遍历根节点）
   遍历结果 3 4 2 6 7 5 1
4. 层次遍历（每层从左到右遍历节点）
   遍历结果为：1 2 5 3 4 6 7

但是从 宏观 角度来看，二叉树的遍历方式分为如下两种

1. 深度优先遍历（DFS）
2. 广度优先比例（BFS）

1.3 二叉树是如何存储的呢？

二叉树的存储方式也可以分为 线性存储 和 链式存储，这里我们以 链式存储 为例。

从上面的图中我们可以分析出，二叉树每个节点至少是有一个数据域，然后还有两个子节点，所以可以构建出如下数据结构

数据结构用代码实现如下

public class TreeNode {
	int val;
	TreeNode left,right;
	public TreeNode(int x) {
        val = x;
        left = null;
        right = null;
    }
}

二、深入理解 BFS

1.1 什么是 BFS

BFS（Breadth First Search） 即广度优先搜索，在数和图中非常常见的一种搜索算法。所谓层次遍历，就是从一个点，向其周围所有的点进行搜索，类似走迷宫，我们在一个点可以进行上下左右的进行选择走。在上面的二叉树中，BFS 是实质就是层次遍历，

1.2 二叉树的层次遍历的原理

二叉树按照从根节点到叶子节点的层次关系，一层向一层横向遍历各个节点。但是二叉树中横向的节点是没有关系的。因此需要借助一个数据结构来辅助工作，这个数据结构是 队列

我们需要借助队列来完成层次遍历的工作，因此

1. 节点 A 入队，得到子节点 B，D ，[A]
2. A 出队，第一个节点是 A ，B、D 入队，得到 [D、B] —— A
3. B 出队，其子节点 C 入队 [C、D] —— A、B
4. D 出队，其子节点 E、F 入队 [C、E、F] —— A、B、D
5. C、E、F 都没有子节点，于是都出队得到 —— A、B、D、C、E、F

2.3 BFS （二叉树层次遍历代码实现）

    public static void cenciTraverseWithQueue(TreeNode root) {
        Queue<TreeNode> queue = new LinkedList<>(); // 创建队列
        queue.offer(root);
        while (!queue.isEmpty()) {
            TreeNode node = queue.poll(); // 元素出队即打印
            System.out.println(node.val); // 打印出队的元素
            if (root.leftNode != null) {
                queue.offer(node.leftNode);
            }
            if (root.rightNode != null) {
                queue.offer(node.rightNode);
            }
        }
    }

三、深入理解 DFS

3.1 什么是 DFS

DFS 即深度优先搜索，同 BFS，在树和图中也是非常常见的。深度优先，就是从一个端点一直查找到另一个端点，“一头深入到底”，在上面的二叉树的遍历中。先序遍历，中序遍历，后序遍历。

3.2 二叉树的 三种遍历方式以及代码实现

给定如下二叉树

3.2.1 先序遍历

递归实现先序遍历

二叉树的先序遍历：

1. 优先访问根节点
2. 然后访问左孩子节点
3. 然后访问右孩子节点。
4. 如果访问的节点既没有左孩子，也没有右孩子，这就说明了到头了，那么就会回到它的父节点，再判断父节点是否有右孩子，依次类推

按照定义：

1. 我们先遍历根节点，即 A
2. 然后判断 A 节点是否有左孩子，即 A B
3. 然而 B节点有孩子节点，所以 B 就作为当前的 根节点， C就作为其左孩子节点，得到 A B C
4. 遍历到 C节点发现到头了，越是往回走，到 B节点，但是发现 B节点也没有 右节点，然后会根节点，发现有右节点，所以得到 A B C D
5. 现在 D作为当前根节点，继续往下走 E，即 A B C D E
   10.E 节点也到头了，所以往回到 D 节点，然后找到 F。即得到 A B C D E F

代码实现：

使用递归我们可以很快的就实现了先序遍历

public class TreeNode {
    // 节点的权
    int val;
    // 左儿子
    TreeNode leftNode;
    // 右儿子
    TreeNode rightNode;
    
    // 前序遍历
    public void frontShow() {
        // 遍历当前节点的内容 (中左右）
        System.out.print(val + " ");

        // 左节点
        if (leftNode != null) {
            leftNode.frontShow();
        }

        // 右节点
        if (rightNode != null)
            rightNode.frontShow();
    }
}

非递归方式实现先序遍历 （栈）

走完一遍递归的节点遍历方式，接下来我们走一遍非递归 的先序遍历。但是我们要使用哪种数据结构来实现 DFS 呢？

答：我们使用递归可以解决的问题，那么就一定有非递归的方法解决问题，在上述的 “遍历过程中” ，有一个重要的点就是，当我们的一个节点访问到头了（这个节点没有子节点），就需要回溯 到上一个节点，然后完成剩下的遍历任务。能够完成回溯任务的是 栈。因此得到一个结论，栈 和 递归都具有回溯的特征。

我们使用栈的后进先出，先进后出的特性

1. 先进入的元素，就可以保存遍历的路径
2. 元素出栈，就实现了回溯到上一个节点
3. 栈保存的就是当前遍历过的所有节点

    // 先序遍历的非递归实现
    public static void preOrderTraverseWithStack(TreeNode root) {
        Stack<TreeNode> stack = new Stack<>();
        TreeNode treeNode = root;
        while (treeNode!=null || !stack.isEmpty()) {
            // 迭代访问节点左孩子，并入栈
            while (treeNode != null) {
                System.out.print(treeNode.val);
                stack.push(treeNode); // 节点入栈
                treeNode = treeNode.leftNode;
            }
            // 如果没有左孩子，则弹出栈顶节点
            if (!stack.isEmpty()) {
                treeNode = stack.pop();
                treeNode = treeNode.rightNode;
            }
        }
    }

3.2.2 中序遍历

原理是一样的，所以就不解释了

递归实现中序遍历

    // 中序遍历 （左根右）
    public void midShow() {
        // 左节点
        if (leftNode != null) {
            leftNode.midShow();
        }

        // 遍历当前节点的内容 (中左右）
        System.out.print(val + " ");

        // 右节点
        if (rightNode != null)
            rightNode.midShow();
    }

非递归实现中序遍历

    public static void midOrderTraverseWithStack(TreeNode root) {
        Stack<TreeNode> stack = new Stack<>();
        TreeNode treeNode = root;
        while (treeNode!=null || !stack.isEmpty()) {
            // 迭代访问节点左孩子，并入栈
            while (treeNode != null) {
                stack.push(treeNode); // 节点入栈
                treeNode = treeNode.leftNode;
            }
            // 如果没有左孩子，则弹出栈顶节点
            if (!stack.isEmpty()) {
                treeNode = stack.pop();
                System.out.print(treeNode.val); // 中序遍历
                treeNode = treeNode.rightNode;
            }
        }
    }

3.2.3 后序遍历

递归实现后续遍历

    public void afterShow() {
        // 左节点
        if (leftNode != null) {
            leftNode.afterShow();
        }

        // 右节点
        if (rightNode != null)
            rightNode.afterShow();

        // 遍历当前节点的内容 (中左右）
        System.out.print(val + " ");
    }

非递归实现后序遍历

参考文章
使用辅助栈实现

    // 后续遍历，左节点，右节点，根节点
    public static void backOrderTraverseWithStack(TreeNode root) {
        Stack<TreeNode> stack = new Stack<>();
        Stack<TreeNode> markStack = new Stack<>(); // 使用辅助栈
        TreeNode treeNode = root;
        while (treeNode!=null || !stack.isEmpty()) {

            while (treeNode != null ) {
                stack.push(treeNode);
                treeNode = treeNode.leftNode;
            }

            while (!markStack.isEmpty() && markStack.peek() == stack.peek()) {
                markStack.pop();
                System.out.println(stack.pop().val); // stack 此时出栈的值即为后序遍历的结果
            }

            if (!stack.isEmpty()) {
                treeNode = stack.peek();
                markStack.push(treeNode);
                treeNode=treeNode.rightNode;
            }
        }
    }