前言

对于刚刚接触深度学习的的童鞋来说，对学习率只有一个很基础的认知，当学习率过大的时候会导致模型难以收敛，过小的时候会收敛速度过慢，其实学习率是一个十分重要的参数，合理的学习率才能让模型收敛到最小点而非局部最优点或鞍点。本文后续内容将会给大家简单回顾下什么是学习率，并介绍如何科学的设置学习率。

什么是学习率

首先我们简单回顾下什么是学习率，在梯度下降的过程中更新权重时的超参数，即下面公式中的$\alpha$

$$\theta =\theta -\alpha \frac{\partial }{\partial \theta }J(\theta )$$

学习率越低，损失函数的变化速度就越慢，容易过拟合。虽然使用低学习率可以确保我们不会错过任何局部极小值，但也意味着我们将花费更长的时间来进行收敛，特别是在被困在局部最优点的时候。而学习率过高容易发生梯度爆炸，loss振动幅度较大，模型难以收敛。下图是不同学习率的loss变化，因此，选择一个合适的学习率是十分重要的。

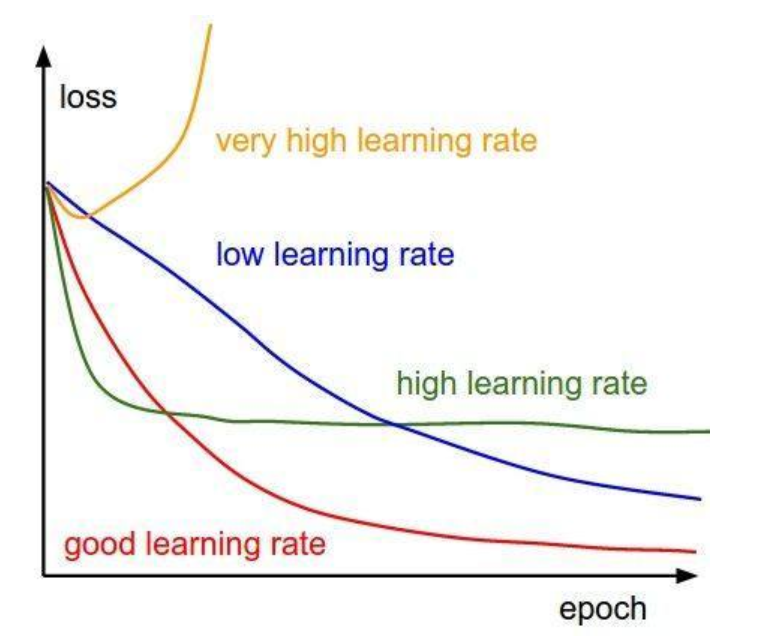
如何设置初始学习率

通常来说，初始学习率以 0.01 ~ 0.001 为宜，但这也只是经验之谈，这里为大家介绍一种较为科学的设置方法。该方法是Leslie N. Smith 在2015年的一篇论文Cyclical Learning Rates for Training Neural Networks中的3.3节提出来的一个非常棒的方法来找初始学习率。该方法很简单，首先设置一个十分小的学习率，在每个epoch之后增大学习率，并记录好每个epoch的loss或者acc，迭代的epoch越多，那被检验的学习率就越多，最后将不同学习率对应的loss或acc进行对比。

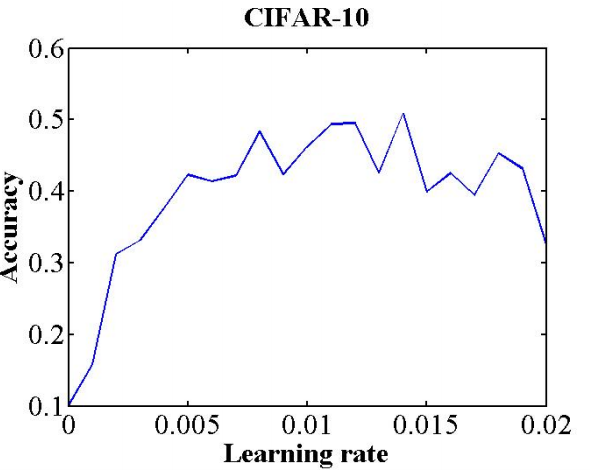
上图是论文中的实验结果，最小学习率是0，最大学习率是0.02，在大概0.01的位置，模型一开始就收敛的很好，因此可以把初始学习率选择为0.01。

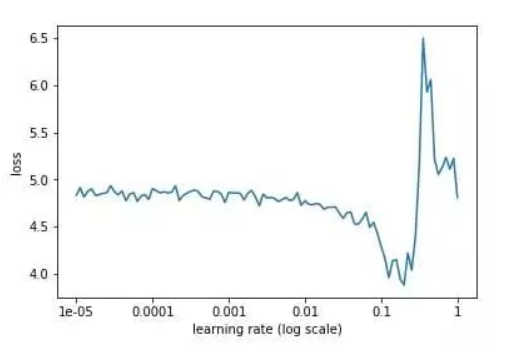
再看下网上找到的另外一张图，从上图可以看到，当学习率从小到大变化的工程中，模型的loss在逐渐减小，但是速度慢，达到某个位置后又会急剧增大，这也对应了我们开头说的学习率小收敛慢，学习率大难以收敛。在这个图中可以很明显的选择一个合适的初始学习率0.1。

要注意一点，选择学习的时候，是从小到大，因为当学习率小的时候对loss影响不会很大，并且学习率比上一轮大，可以看做是在原始数据进行更新，如果一开始学习率很大对loss影响是很大的，这个时候再来选择初始学习率那就是无稽之谈了。

学习率衰减

通常在训练一定epoch之后，都会对学习率进行衰减，从而让模型收敛得更好。学习率衰减有以下三种方式：

• 轮数衰减：每经过n个epochs后学习率减半
• 指数衰减：每经过n个epochs后学习率乘以一个衰减率
  $${\alpha }_t=0.95^{epoch}\ast {\alpha }_{t-1}$$
• 分数衰减：和指数衰减类似，不过公式不太一样
  $${\alpha }_t=\frac{{\alpha }_{t-1}}{1+delay\_rate\ast epoch}$$

学习率衰减的缺点

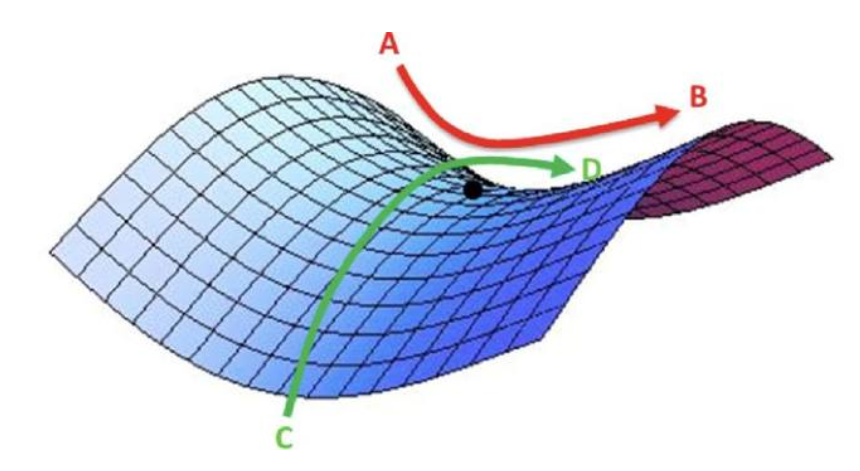
虽然采用学习率衰减的方法能让模型收敛的更好，但是如果遇到鞍点的时候，模型就没法继续收敛，如下图所示，黑点即是鞍点，如果学习率此时很小，那将永远无法走出鞍点。

Cyclical Learning Rates(CRL)

那么怎么解决这个鞍点的问题，这叫要回到我们上文说到过的论文中了，这篇论文的主要内容其实就是介绍了一种方法，能在遇到鞍点时尽快从中走出去，该方法称为Cyclical Learning Rates，其思想如下，首先论文中提出了两个参数，base_lr和max_lr，我们继续以之前的图讲解，

在0.005的位置，开始出现了acc的负增长之后并趋于平缓，这个点即可作为max_lr，base_lr通常是设置为max_lr的1/3或1/4，因此0.001可以作为base_lr。

接下来就根据这两个参数进行实时的学习率的计算，论文中提到了三种更新学习率的方法：

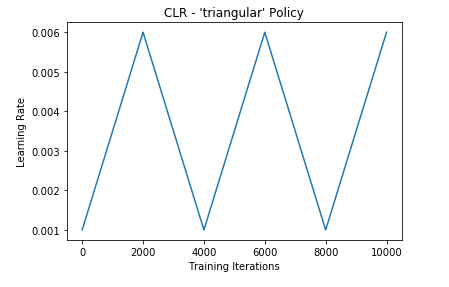
• triangular
  
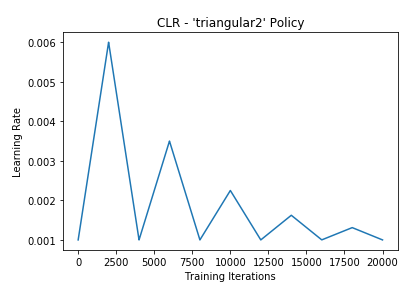
• triangular2
  
• exp range
  

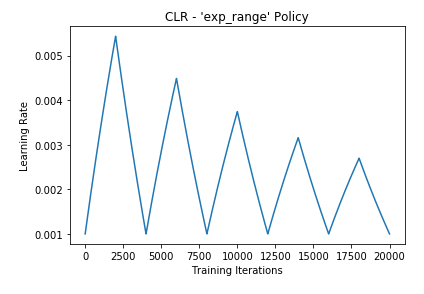
从图中可以看到，第一种方法只是在最大学习率与最小学习率中进行选择，第二种和第三种方法会对max_lr进行衰减。

三种计算方法其实都不复杂且效率很高，计算公式如下

cycle = np.floor(1+iterations/(2*step_size))
x = np.abs(iterations/step_size - 2*cycle + 1)
lr= base_lr + (max_lr-base_lr)*np.maximum(0, (1-x))*scale_fn(x)

其中iterations表示的是当前迭代的步数，注意不是epochs，step_size表示的是每隔多少步数进行一次学习率的调整，这个值通常是每个epoch的步数steps的2-10倍，例如每个epoch是500步，那step_size可以选择2000，三种方法的不同之处就在于scale_fn：

• triangular
  $$scale\_fn=1$$

• triangular2
  $$scale\_fn=\frac{1}{2^{(cycle-1)}}$$

• exp range
  $$scale\_fn={\gamma }^{steps}$$

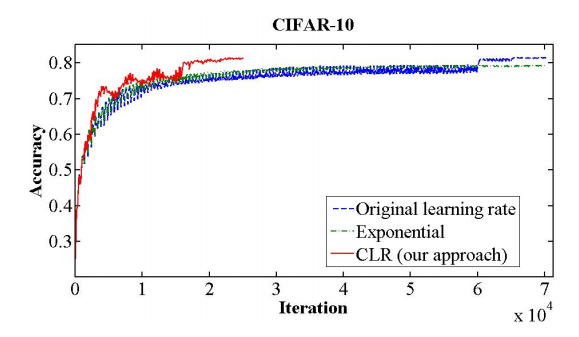
下图是CLR和其他情况的对比，可以看到CLR的收敛速度明显优于其他方法，而其中的acc的波动也是因为学习率变大引起的，但是对最终的结果并没有影响。

参考文献

Cyclical Learning Rates for Training Neural Networks