一、实验目的

（1）掌握 求系统响应的方法。

（2）掌握时域离散系统的时域特性。

（3）分析、观察及检验系统的稳定性。

二、实验原理与方法

在时域中，描写系统特性的方法是差分方程和单位脉冲响应，在频域可以用系统函数描述系统特性。已知输入信号可以由差分方程、单位脉冲响应或系统函数求出系统对于该输入信号的响应，本实验仅在时域求解。在计算机上适合用递推法求差分方程的解，最简单的方法是采用MATLAB语言的工具箱函数filter函数。也可以用MATLAB语言的工具箱函数conv函数计算输入信号和系统的单位脉冲响应的线性卷积，求出系统的响应。

系统的时域特性指的是系统的线性时不变性质、因果性和稳定性。重点分析实验系统的稳定性，包括观察系统的暂态响应和稳定响应。

系统的稳定性是指对任意有界的输入信号，系统都能得到有界的系统响应。或者系统的单位脉冲响应满足绝对可和的条件。系统的稳定性由其差分方程的系数决定。

实际中检查系统是否稳定，不可能检查系统对所有有界的输入信号，输出是否都是有界输出，或者检查系统的单位脉冲响应满足绝对可和的条件。可行的方法是在系统的输入端加入单位阶跃序列，如果系统的输出趋近一个常数（包括零），就可以断定系统是稳定的。系统的稳态输出是指当n趋于时，系统的输出。如果系统稳定，信号加入系统后，系统输出的开始一段称为暂态效应，随n的加大，幅度趋于稳定，达到稳态输出。

注意在以下实验中均假设系统的初始状态为零

三、实验内容与步骤

编制程序，包括产生输入信号、单位脉冲响应序列的子程序，用filter函数或conv函数求解系统输出响应的主程序。程序中要有绘制信号波形的功能。

1.给定一个低通滤波器的差分方程为

2.给定系统的单位脉冲响应为 

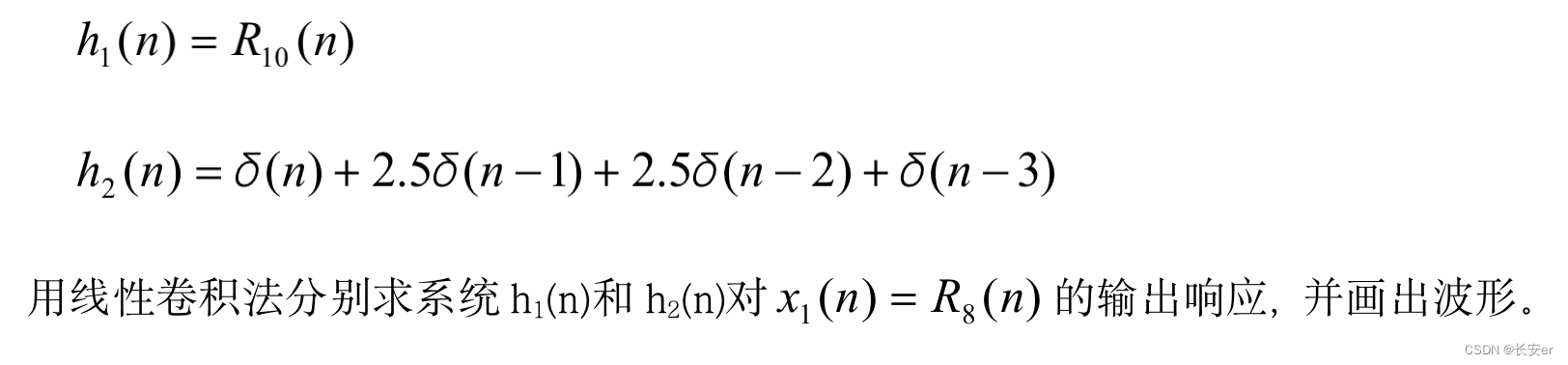3.给定一谐振器的差分方程为

 

四、实验结果与分析

1.给定一个低通滤波器的差分方程为

（1）实验源代码

1.%调用filter解差分方程，由系统对u(n)的响应判断稳定性
2. %系统差分方程系数向量B和A
3.A=[1, -0.9]; B=[0.05, 0.05];   
4. %产生信号x1n=R8n 
5.x1n=[1 1 1 1 1 1 1 1 zeros(1, 50)];
6. %产生信号x2n=un
7.x2n=ones(1, 128);   
8.%求系统单位脉冲响应h(n)
9.hn=impz(B, A, 58);             
10.%调用函数stem绘图    
11.subplot(2, 2, 1),y='h(n)';stem(hn);
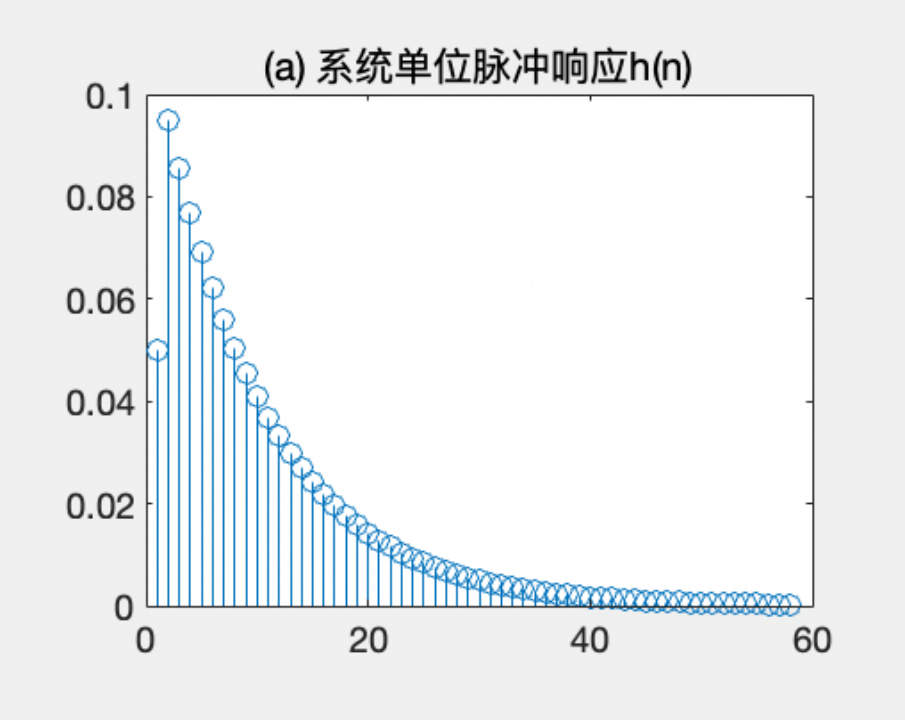
12.title('(a) 系统单位脉冲响应h(n)')
13.  %求系统对x1n的响应y1n
14.y1n=filter(B, A, x1n);          
15.subplot(2, 2, 2); y='y1(n)'; stem(y1n); 
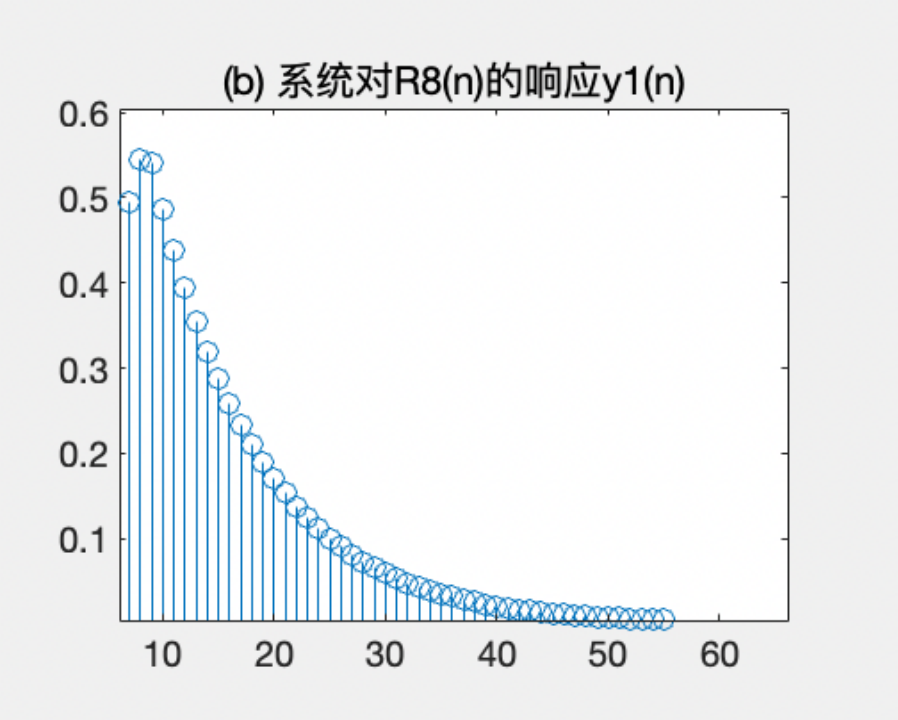
16.title('(b) 系统对R8(n)的响应y1(n)')
17.  %求系统对x2n的响应y2n
18.y2n=filter(B, A, x2n);           
19.subplot(2, 2, 4); y='y2(n)'; stem(y2n); 
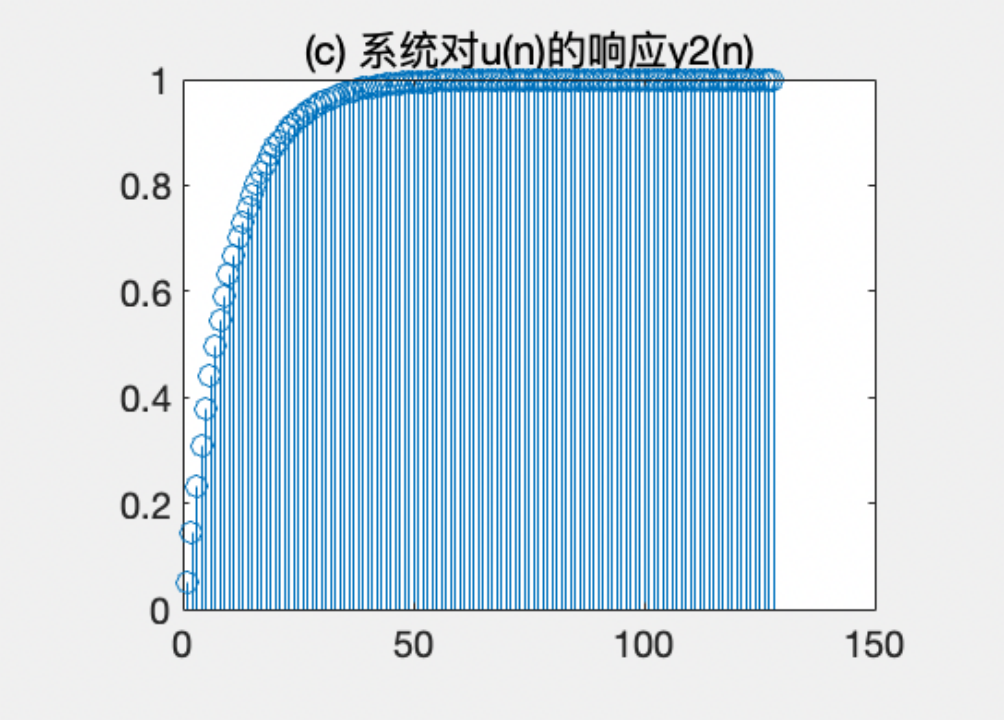
20.title('(c) 系统对u(n)的响应y2(n)')

（2）程序运行波形

图I 系统对的响应序列

图II 系统对的响应序列

图III 系统的单位脉冲响应的波形

（3）结果分析

首先这段代码主要分为以下几个部分：

·定义系统差分方程系数向量 A和 B；

· 产生输入信号 x1(n)和 x2(n)；

· 求解系统的单位脉冲响应 h(n)h(n)；

·使用 filter 函数求解系统对输入信号的响应 y1(n) 和 y2(n)；

·绘制系统的单位脉冲响应图、系统对 x1(n) 的响应图和系统对 x2(n) 的响应图。

其中，系统差分方程为：

 

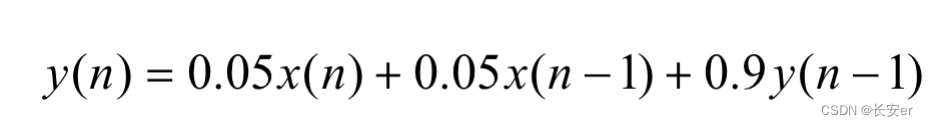
从差分方程可以看出，该系统是一个有限脉冲响应（FIR）系统，因为其只和输入信号的过去时刻有关，和未来时刻无关。

在这个代码中，我们使用了 filter 函数来求解系统的响应。filter 函数是 MATLAB 中用于离散时间信号滤波的函数，其输入参数为：系统传递函数的分母系数 AA、分子系数 BB 和输入信号（以向量形式输入），输出参数为离散时间信号滤波器的输出响应。因此，我们可以使用 filter 函数方便地求解系统对输入信号的响应。

下面我们来分析这段代码中绘制的波形图：

图I显示系统对的响应序列，从图中可以看出，由于输入信号是 R8 序列，其包含频率高的成分。在该系统的作用下，高频成分被滤掉，输出信号幅度逐渐趋向于稳定；

• 图II显示了系统对的响应序列。从图中可以看出，由于输入信号是 R8 序列，其包含频率高的成分。在该系统的作用下，高频成分被滤掉，输出信号幅度逐渐趋向于稳定；
• 图III 显示了系统的单位脉冲响应，其基本形状为一个振荡衰减的函数；

因此，我们可以通过使用 filter 函数来求解系统的响应，并利用系统对不同类型输入信号的响应判断其是否稳定。

2.给定系统的单位脉冲响应为

 

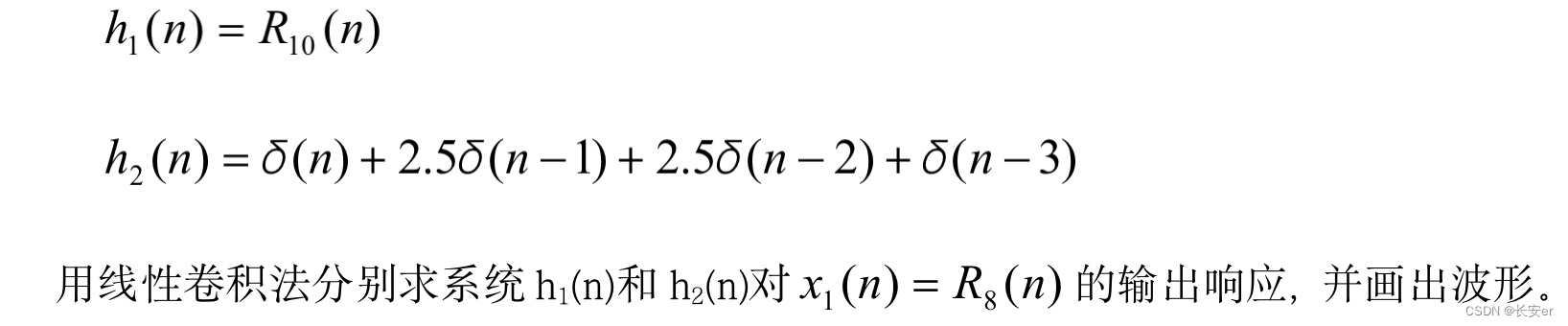
（1）程序源代码

1.%产生信号x1n=R8n
2.x1n=[1 1 1 1 1 1 1 1 ]; 
3.%产生h1n信号   
4.h1n=[ones(1, 10) zeros(1, 10)];
5.%产生h2n信号
6.h2n=[1 2.5 2.5 1 zeros(1, 10)]; 
7.%调用conv函数求解系统输出响应
8.y21n=conv(h1n, x1n); 
9.y22n=conv(h2n, x1n); 
10.figure(2)
11.subplot(2, 2, 1); y='h1(n)'; stem(h1n);%调用函数stem绘图
12.title('(d) 系统单位脉冲响应h1(n)')
13.subplot(2, 2, 2); y='y21(n)'; stem(y21n);
14.title('(e) h1(n)与R8(n)的卷积y21(n)')
15.subplot(2, 2, 3);y='h2(n)';stem(h2n);%调用函数stem绘图
16.title('(f) 系统单位脉冲响应h2(n)')
17.subplot(2, 2, 4); y='y22(n)'; stem(y22n);
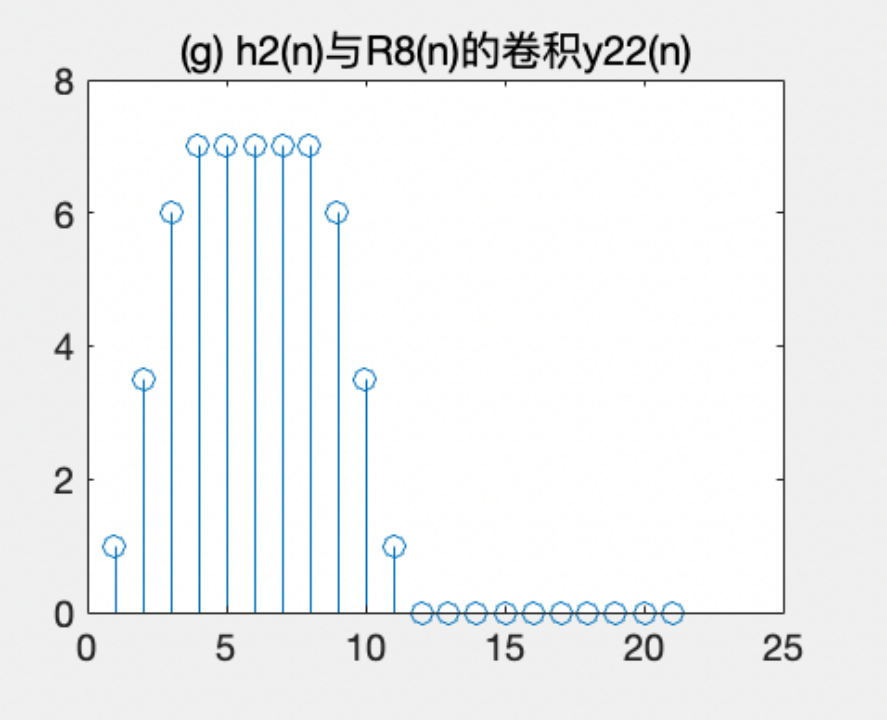
18.title('(g) h2(n)与R8(n)的卷积y22(n)')

（2）程序运行波形

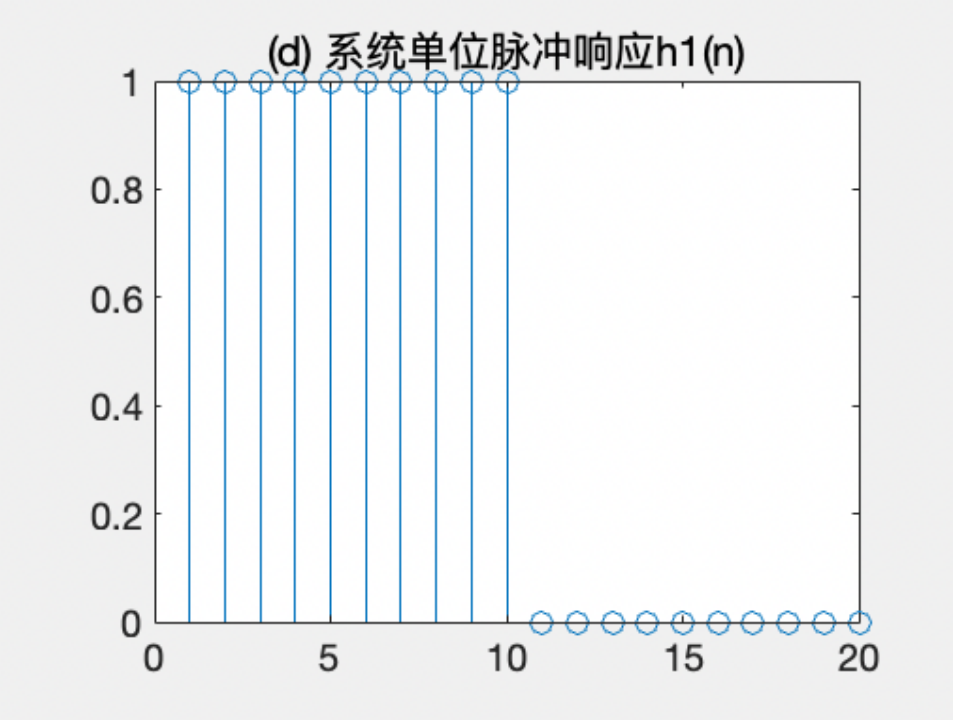
图I 系统单位脉冲响应h1(n)

图II 系统单位脉冲响应h2(n)

 

 

 

（3）结果分析

这段代码及实验主要是对一个LTI系统的单位脉冲响应和对不同输入信号的响应进行分析。具体的分析如下：

·产生输入信号 x1(n)，其为包含8个元素的向量，每个元素的值均为

·产生单位脉冲响应 h1(n)，其为一个包含20个元素的向量，前10个元素的值为1，后10个元素的值为0。

·产生另一个单位脉冲响应 h2(n)，其为一个包含15个元素的向量，前4个元素的值依次为1，2.5，2.5，1，后面11个元素的值为0。

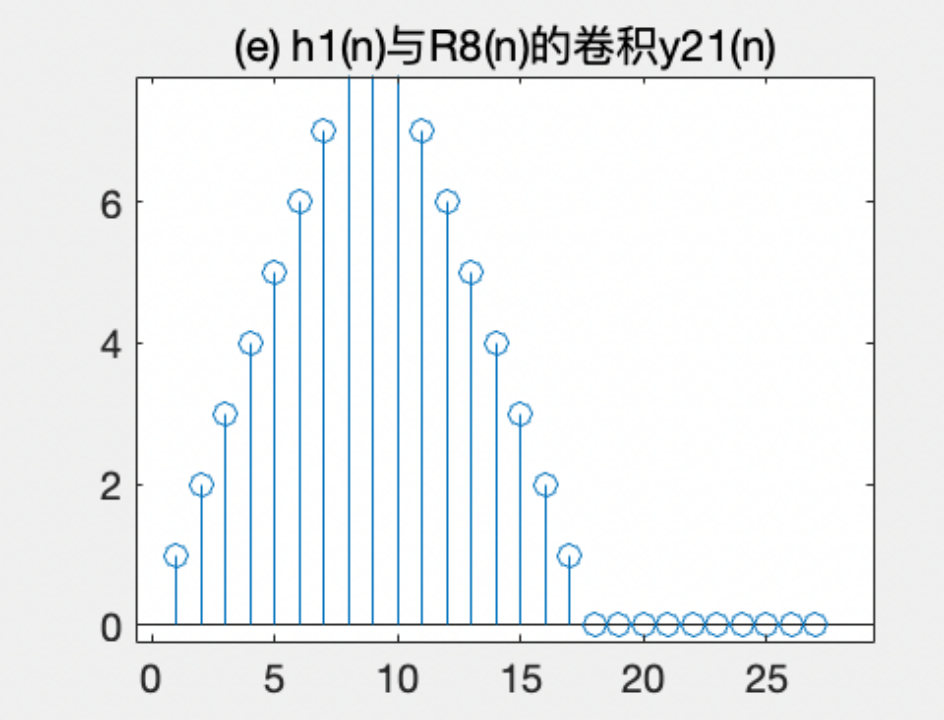
使用 conv 函数求解系统对输入信号的响应，将得到的输出信号保存在变量 y21(n) 和 y22(n) 中。其中，y21(n)表示系统对输入信号 x1(n)和单位脉冲响应 h1(n)的卷积结果，y22(n)则表示系统对输入信号 x1(n)和单位脉冲响应 h2(n)的卷积结果。

绘制四张的图表，分别显示：系统的单位脉冲响应 h1(n)、系统对输入信号 x1(n)和 h1(n)的卷积结果 y21(n)、系统的单位脉冲响应 h2(n)，以及系统对输入信号 x1(n)和 h2(n)的卷积结果 y22(n)。在图表中使用 subplot 函数将四张图表排列在一起，并使用 stem 函数以离散形式绘制图像。从这段代码中可以看出，使用卷积运算可以求解LTI系统对不同输入信号的响应。单位脉冲响应则是一种很特殊的输入信号，通过对其进行卷积得到的输出信号称为系统的“impulse response”或者“unit sample response”，它显示了系统对单个单位脉冲的响应情况。而系统对其他信号的响应则可以类比为对单位脉冲响应的加权叠加，因此可以通过对单位脉冲响应进行卷积得到。因此，本实验通过对两个不同的单位脉冲响应和一个输入信号进行卷积，得到了LTI系统对不同信号的响应情况，并通过图表的方式进行了可视化展示。

3.给定一谐振器的差分方程为 

（1）实验代码

1.%产生信号un
2.un=ones(1, 256);    
3.n=0:255; 
4.%产生正弦信号
5.xsin=sin(0.014*n)+sin(0.4*n);  
6.A=[1, -1.8237, 0.9801]; 
7.B=[1/100.49, 0,-1/100.4];   
8.%系统差分方程系数向量B和A
9.y31n=filter(B, A, un);      
10. %谐振器对un的响应y31n
11.y32n=filter(B, A, xsin);  
12.%谐振器对正弦信号的响应y32n
13.figure(3)
14.%调用函数stem绘图
15.subplot(2, 1, 1); y='y31(n)'; stem(y31n)
16.title('(h) 谐振器对u(n)的响应y31(n)')
17.%调用函数stem绘图
18.subplot(2, 1, 2); y='y32(n)'; stem(y32n); 
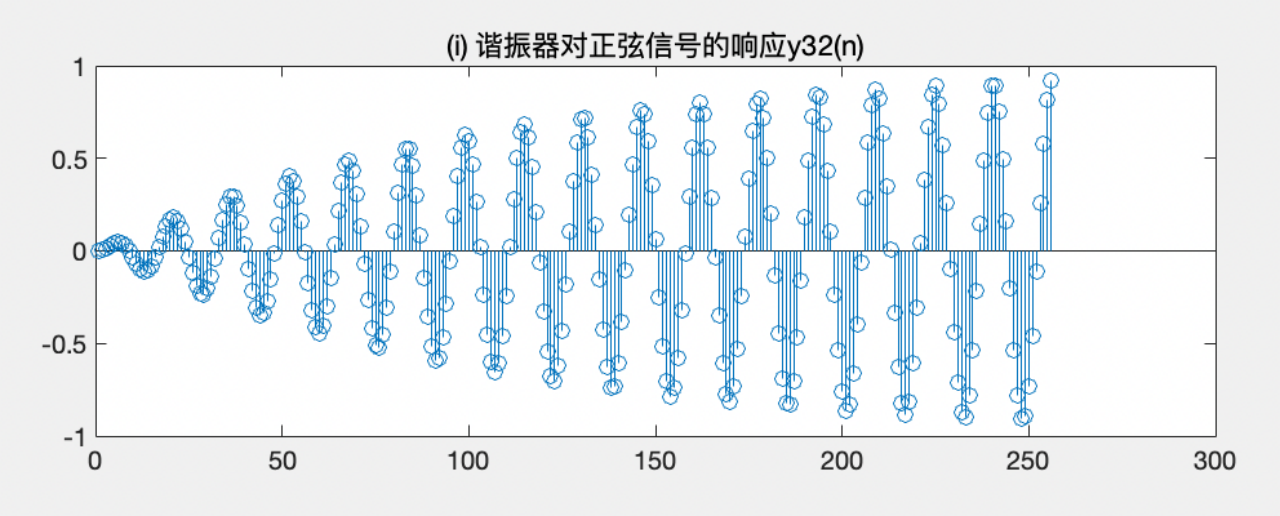
title('(i) 谐振器对正弦信号的响应y32(n)')

（2）程序运行截图

图I 谐振器对x(n)的响应y32(n)

 

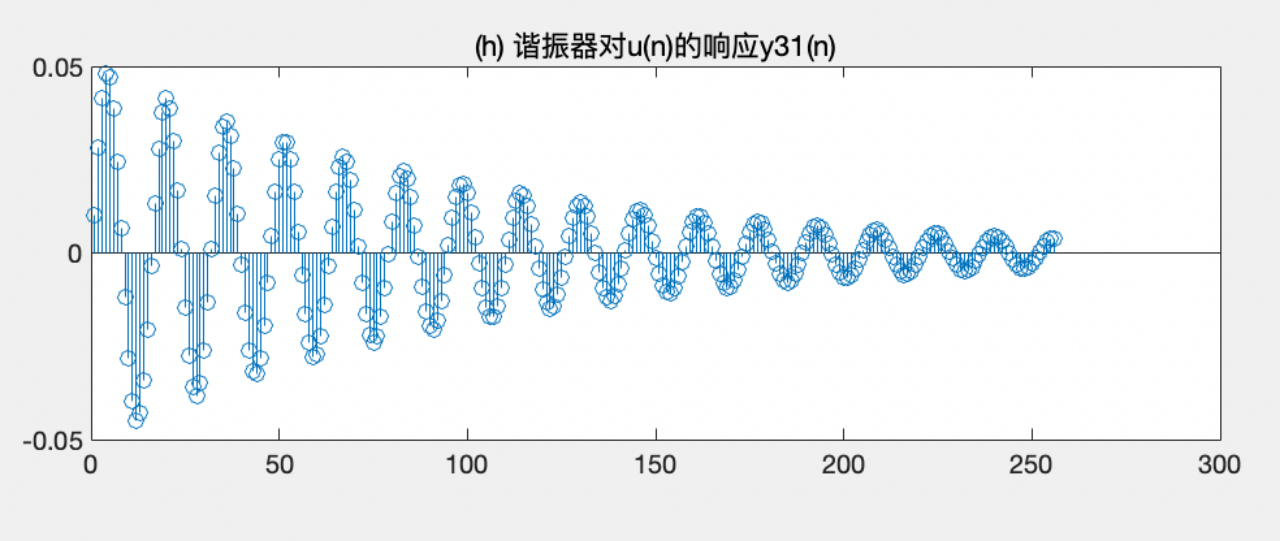
图II 谐振器对u(n)的响应y31(n)

（3）结果分析

这段代码是一个MATLAB程序，主要用于实现一个谐振器系统对单位脉冲信号和正弦信号的响应分析，并通过使用 stem 函数将结果以离散的形式绘制在两个图表中。

具体分析如下：

·定义一个包含256个元素的向量 un 和一个从0到255的整数序列 n，其中 un 所有元素的值都为1，所以 un 是一个单位脉冲信号。

·通过使用两个不同频率的正弦波按照一定比例叠加而成的方式产生一个包含256个元素的正弦信号 xsin，其中每个元素的值由两个正弦波叠加而成。这个信号将被用于测试谐振器系统对非周期性的任意输入信号的响应情况。

·定义两个向量B和A，用于表示谐振器差分方程的系数。这个差分方程代表了谐振器系统的动态行为，控制着系统对输入信号的响应情况。其中，向量B表示的是与输出项相关的系数，而向量A则表示的是与输入项相关的系数。

·通过使用 filter 函数对谐振器系统进行模拟计算，得到谐振器对输入信号 un 和正弦信号 xsin 的响应结果，分别保存在 y31n 和 y32n 两个向量中。其中，y31n 表示谐振器对 un 的响应，而 y32n 则表示谐振器对 xsin 的响应。

最后，通过使用 subplot 和 stem 函数将谐振器对输入信号和正弦信号的响应结果绘制成两张图表，并在图表中加入标题以及其他必要的注释信息。

从这段代码中可以看出，该系统是一个谐振器系统，通过控制差分方程的系数，可以改变系统对不同输入信号的响应特性。谐振器系统在一定条件下是稳定的，具体条件与系统的参数有关。谐振器具有对某个频率进行谐振的性质，本实验中的谐振器的谐振频率是0.4 rad,因此稳定波形为sin(0.4n)。

五、实验思考

1. 在时域求系统响应的方法

在时域求系统响应的方法通常分为两类，一类是利用微分方程或差分方程求解的方法，另一类则是基于卷积定理的方法。

利用微分方程求解的方法：该方法适用于已知系统微分方程的情况下，可以通过对方程进行变换和求解，得到系统在时域的响应。具体步骤如下：

(1) 根据系统的微分方程和初始条件，列出完整的系统方程；

(2) 对系统方程进行变换得到其特征方程，并求出特征根；

(3) 根据特征根分类讨论系统在不同情况下的稳定性和响应特性；

(4) 根据初始条件和输入信号，求解出系统的响应公式。

对于连续时间系统，通常使用微分方程来描述，而对于离散时间系统，则通常使用差分方程来描述。利用微分方程或差分方程求解时域系统响应的基本步骤是相似的。在差分方程的情况下，需要根据差分方程对输入信号进行离散化，然后通过对差分方程进行变换和求解，得到系统在时域的响应。

基于卷积定理的方法：该方法适用于已知系统冲击响应的情况下，可以通过将输入信号和系统冲击响应进行卷积，得到系统在时域的响应。具体步骤如下：

(1) 根据系统差分方程，求出系统的冲击响应函数或单位脉冲响应函数；

(2) 将输入信号和系统的冲击响应函数或单位脉冲响应函数进行卷积运算，得到系统在时域的响应。

以上是两种常见的求解系统时域响应的方法，其适用范围有所不同。需要根据具体问题和条件选择合适的方法进行求解。

2.如何通过实验判断系统稳定性

系统的稳定性是否能通过实验来判断，取决于所研究的系统类型和实验条件。 一般来说，有两种方法可以通过实验判断系统稳定性：

（1）输入输出试验法：该方法是通过对系统输入信号进行变化，观察系统输出响应的变化情况，判断系统是否稳定。具体来说，可以通过以下步骤来进行实验：

(1) 对系统进行较小幅度的输入变化，如阶跃信号或正弦信号；

(2) 观察系统输出响应的变化情况，如过渡过程的持续时间、振荡的频率、振幅等；

(3) 根据输出信号的变化情况，判断系统的稳定性。

如果系统在输入变化后，输出信号能够逐渐趋于稳定且不产生超调、振荡等异常现象，则可以认为系统是稳定的。

（2）极点分布法：该方法是通过测量系统传递函数的极点位置，判断系统是否稳定。具体来说，可以通过以下步骤来进行实验：

(1) 测量系统的传递函数；

(2) 分析传递函数的极点位置和极点个数，根据极点位置判断系统的稳定性；

(3) 如果所有极点都位于左半平面，则系统是稳定的；如果存在极点位于右半平面，则系统不稳定。

需要注意的是，实验测量所得的结果受到实验条件和测量误差的影响，因此需要进行多次实验，并对实验数据进行统计分析，以提高实验的可靠性。

3.在分析理想采样序列特性的实验中

采样频率不同时，相应理想采样序列的傅里叶变换频谱的数字频率度量是否都相同? 它们所对应的模拟频率是否相同? 为什么?

在分析理想采样序列特性的实验中，相应理想采样序列的傅里叶变换频谱的数字频率度量不同，但它们所对应的模拟频率是相同的。

数字频率是以采样周期为单位的频率。当采样频率不同时，数字频率的单位和取值范围都会发生实质性变化。例如，在采样频率为 fs1 时，数字频率的最大值为 fs1/2，单位是 Hz/sample；而在采样频率为 fs2 时，数字频率的最大值为 fs2/2，单位同样是 Hz/sample。因此，相应的理想采样序列的傅里叶变换频谱的数字频率度量不同，即对应不同的频率坐标轴。

然而，它们所对应的模拟频率是相同的，即原信号的频率。这是因为采样定理要求采样频率至少是原信号的 2 倍，因此无论采样频率取多少，采样得到的离散信号所包含的信息都与原信号的频率相同。因此，在分析理想采样序列特性时，可以忽略数字频率的变化，只需关注其所对应的模拟频率即可。

六、实验总结

第一次数字信号处理实验，从平时的理论课过渡到实验课，很有一番新奇。通过利用Matlab对书本上问题进行编程解决，让我对此类问题的本质有了新的理解，也让我对课本上的知识有了更深一步的认识。

本次实验通过编写程序，产生输入信号并求出系统对其的响应，进一步掌握了求解时域离散系统特性的方法和分析、观察及检验系统稳定性的技巧。实验中重点探究了系统稳定性的判断方法和在时域求解系统响应的两种常见方法，以及思考了理想采样序列特性和卷积定理的验证等。值得注意的是，在实验过程中，需要注意选取合适的采样频率和采样点数，以确保实验数据的准确性。

通过本次实验，不仅进一步加深了对时域离散系统特性和系统稳定性的理解，通过对Matlab的利用，也提高了编程能力和实验操作技能，熟悉了Matlab语言的语法和用法。同时，也意识到了科学实验中精细化操作和数据处理的重要性，这也为日后的科学研究打下了坚实的基础。