神经网络详解(基本完成)
#Fill you up with petrol
#概述
人工神经网络(artificial neural network,ANN),简称神经网络(neural network,NN),是一种模仿生物神经网络的结构和功能的数学模型或计算模型。神经网络由大量的人工神经元联结进行计算。大多数情况下人工神经网络能在外界信息的基础上改变内部结构,是一种自适应系统。现代神经网络是一种非线性统计性数据建模工具,常用来对输入和输出间复杂的关系进行建模,或用来探索数据的模式。
神经网络是一种运算模型,由大量的节点(或称“神经元”)和之间相互的联接构成。每个节点代表一种特定的输出函数,称为激励函数、激活函数(activation function)。每两个节点间的联接都代表一个对于通过该连接信号的加权值,称之为权重,这相当于人工神经网络的记忆。网络的输出则依网络的连接方式,权重值和激励函数的不同而不同。而网络自身通常都是对自然界某种算法或者函数的逼近,也可能是对一种逻辑策略的表达。
它的构筑理念是受到生物(人或其他动物)神经网络功能的运作启发而产生的。人工神经网络通常是通过一个基于数学统计学类型的学习方法得以优化,所以人工神经网络也是数学统计学方法的一种实际应用,通过统计学的标准数学方法我们能够得到大量的可以用函数来表达的局部结构空间,另一方面在人工智能学的人工感知领域,我们通过数学统计学的应用可以来做人工感知方面的决定问题(也就是说通过统计学的方法,人工神经网络能够类似人一样具有简单的决定能力和简单的判断能力),这种方法比起正式的逻辑学推理演算更具有优势。
神经网络最重要的用途是分类,为了让大家对分类有个直观的认识,咱们先看几个例子:
- 垃圾邮件识别:现在有一封电子邮件,把出现在里面的所有词汇提取出来,送进一个机器里,机器需要判断这封邮件是否是垃圾邮件。
- 疾病判断:病人到医院去做了一大堆肝功、尿检测验,把测验结果送进一个机器里,机器需要判断这个病人是否得病,得的什么病。
- 猫狗分类:有一大堆猫、狗照片,把每一张照片送进一个机器里,机器需要判断这幅照片里的东西是猫还是狗。
#分类器
向上例这种能自动对输入的东西进行分类的机器,就叫做分类器。
分类器的输入是一个数值向量,叫做特征(向量)。
就是线性代数中学到地特征向量,若果不懂会去看书,或者看这里:
特征值和特征向量(简易版)。
上面两个是同一个答主(马同学),寻根溯源,细致入微,比我自己总结的好。
若要全面认识神经网络,我觉得这一点基础还是要有的,请不要忽视。
在垃圾邮件识别里,分类器的输入是一堆0、1值,表示字典里的每一个词是否在邮件中出现,比如向量(1,1,0,0,0…)就表示这封邮件里只出现了两个词abandon和abnormal;第二个例子里,分类器的输入是一堆化验指标;第三个例子里,分类器的输入是照片,假如每一张照片都是320240像素的红绿蓝三通道彩色照片,那么分类器的输入就是一个长度为320240*3=230400的向量。
分类器的输出也是数值。第一个例子中,输出1表示邮件是垃圾邮件,输出0则说明邮件是正常邮件;第二个例子中,输出0表示健康,输出1表示有甲肝,输出2表示有乙肝,输出3表示有饼干等等;第三个例子中,输出0表示图片中是狗,输出1表示是猫。
分类器的目标就是让正确分类的比例尽可能高。一般我们需要首先收集一些样本,人为标记上正确分类结果,然后用这些标记好的数据训练分类器,训练好的分类器就可以在新来的特征向量上工作了。
同上,引用自知乎:如何简单形象又有趣地讲解神经网络是什么?
答主:王小龙
#神经元(生物学)
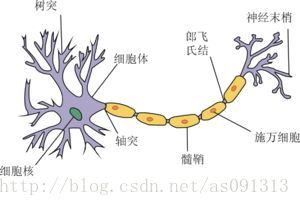
先来看一下生物学上的神经元:
先凑合着看,画质不好。
正如高中生物所学,
神经元大致可以分为树突、突触、细胞体和轴突。树突为神经元的输入通道,其功能是将其他神经元的动作电位传递至细胞体。其他神经元的动作电位借由位于树突分支上的多个突触传递至树突上。
神经细胞可以视为有两种状态的机器,激活时为“是”,不激活时为“否”。神经细胞的状态取决于从其他神经细胞接收到的信号量,以及突触的性质(抑制或加强)。当信号量超过某个阈值( Threshold )时,细胞体就会被激活,产生电脉冲。电脉冲沿着轴突并通过突触传递到其它神经元。
来源:维基百科
#M-P神经元模型
##作用
接受其他多个神经元传入的信号,然后将这些信号汇总成总信号,对比总信号与阈值,如果超过阈值,则产生兴奋信号并输出出去,如果低于阈值,则处于抑制状态。
一条直线把平面一分为二,一个平面把三维空间一分为二,一个 n − 1 n-1 n−1 维超平面把 n n n 维空间一分为二,两边分属不同的两类,这种分类器就叫做神经元。
大家都知道平面上的直线方程是 a x + b y + c = 0 ax+by+c=0 ax+by+c=0,等式左边大于零和小于零分别表示点 ( x , y ) (x,y) (x,y)在直线的一侧还是另一侧,把这个式子推广到n维空间里,直线的高维形式称为超平面,它的方程是:
h = a 1 x 1 + a 2 x 2 + . . . + a n x n + a 0 = 0 h = a_1x_1+a_2 x_2+...+a_nx_n+a_0=0 h=a1x1+a2x2+...+anxn+a0=0
神经元就是当h大于0时输出1,h小于0时输出0这么一个模型,它的实质就是把特征空间一切两半,认为两瓣分别属两个类。
##构造
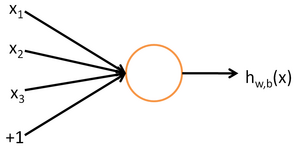
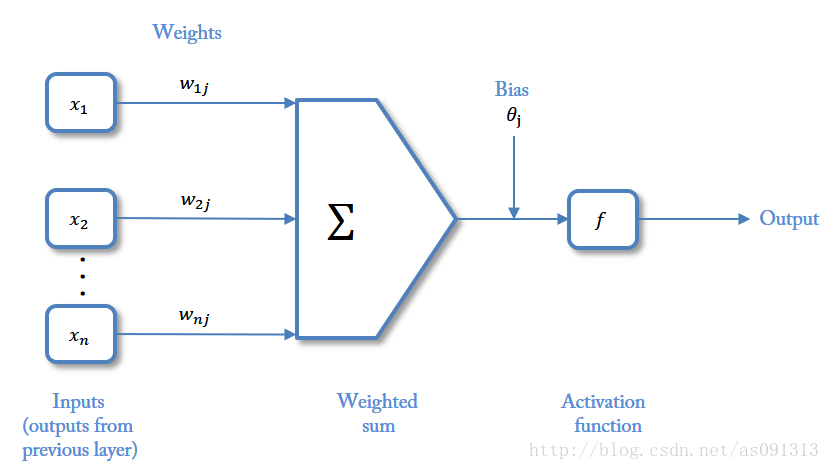
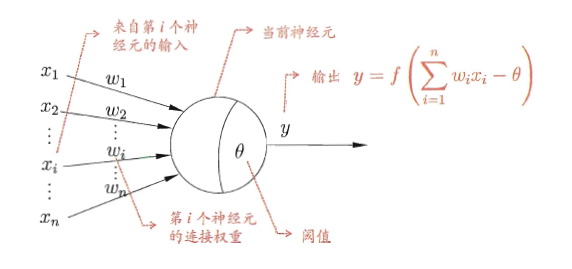
上图:
这个是我最喜欢的的关于神经元的图示(自己高清重置版)。
I n p u t s Inputs Inputs:输入。
W e i g h t s Weights Weights:权值,权重。
B i a s Bias Bias:偏置,或者称为阈值 ( T h r e s h o l d ) ( Threshold ) (Threshold)。
A c t i v a t i o n f u n c t i o n Activation function Activationfunction:激活函数。
这种“阈值加权和”的神经元模型称为M-P模型 ( McCulloch-Pitts Model ),也称为神经网络的一个处理单元( PE, Processing Element )。
###其他图示
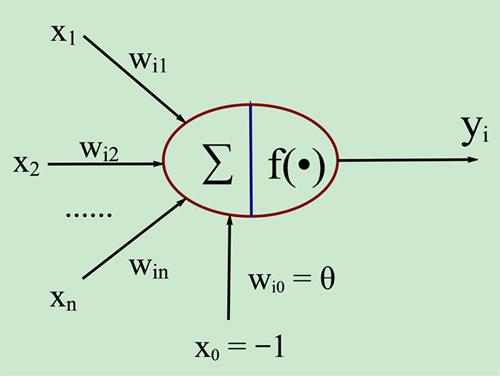 ###输入
###输入
输入的是特征向量,通过对其的学习,可以得知,特征向量代表的是变化的方向。
或者说,是最能代表这个事物的特征的方向。
人有性别,身高,手,脚,五官等。
电脑有屏幕,键盘,CPU,GPU等。
速度有方向。
颜色有种类。
特别是速度的方向,物理中总是用一个矢量箭头代表方向,速度改变最大(增加或减少)的方向。(所以后面要 求导数)
玄之又玄,众妙之门。
好好揣摩吧。
###权重(权值)
就是特征值嘛,输入是特征向量,权重和它相乘,那不就对应特征值么。
有正有负,加强或抑制,同特征值一样。
权重的绝对值大小,代表了输入信号对神经元的影响的大小。
正如上面的例子,输入一张图片,判断是是猫还是犬。
第一层输入的有毛发,爪子,牙齿类型等。
第二层有头部,腹部,腿部等。
牙齿对腿部的影响就会比较小啊,牙齿和腿部之间的权重的绝对值就会小一些,诸如此类。
还有另外的解释,上面如何简单形象又有趣地讲解神经网络是什么?中,我上面引用的是赞数最高的回答,赞数第二高的回答,答主:YJango 的回答,虽然略有些晦涩难懂,但我希望你能看一看,思考思考。
我们要割一刀,得有割的角度和方向,而权重,就负责调整方向,这和特征向量的方向是两回事。
按答主:YJango 的方向来看, n n n维空间中,乘以权重就好像是在不断的扭曲空间(空间变换),使不同类别的事物被扭曲到不同的一侧,来找到一个合适的 n − 1 n-1 n−1维超平面。
###偏置(阈值)
上面的神经元的图示,我们总是减去 θ \theta θ,说得通俗点,要证明 a > b a > b a>b可以证明 a − b > 0 a - b > 0 a−b>0。
###激活函数(传输函数)
####线性函数
#####线性函数
f ( x ) = k x + c f(x)=kx+c f(x)=kx+c
#####斜面函数
f ( x ) = { T x > c k x ∣ x ∣ ⩽ c − T x < − c f(x)=\left\{ \begin{array}{rcl} T & & {x > c}\\ kx & & {|x|\leqslant c}\\ -T & & {x <-c}\\ \end{array} \right. f(x)=⎩⎨⎧Tkx−Tx>c∣x∣⩽cx<−c
#####阈值函数
f ( x ) = { 1 x ⩾ c 0 x < c f(x)=\left\{ \begin{array}{rcl} 1 & & {x\geqslant c}\\ 0 && {x<c}\\ \end{array}\right. f(x)={10x⩾cx<c
####非线性函数
#####S型函数(Sigmoid函数)
f ( x ) = 1 1 + e − α x ( x ∈ R ) f(x)=\frac{1}{1+e^{-\alpha x}} \space (x \in R) f(x)=1+e−αx1 (x∈R)
#####Sigmoid函数导数
f ′ ( x ) = α e − α x ( 1 + e − α x ) 2 = α f ( x ) [ 1 − f ( x ) ] f'(x)=\frac{\alpha e^{-\alpha x}}{(1+e^{-\alpha x})^2}=\alpha f(x)[1-f(x)] f′(x)=(1+e−αx)2αe−αx=αf(x)[1−f(x)]
#####双极性Sigmoid函数
h ( x ) = 2 1 + e − α x − 1 ( x ∈ R ) h(x)=\frac{2}{1+e^{-\alpha x}} \space -1 \space\space(x \in R) h(x)=1+e−αx2 −1 (x∈R)
#####双极性Sigmoid函数导数
h ′ ( x ) = 2 α e − α x ( 1 + e − α x ) 2 = α 1 − h ( x ) 2 2 h'(x)=\frac{2\alpha e^{-\alpha x}}{(1+e^{-\alpha x})^2}=\alpha \frac{1-h(x)^2}{2} h′(x)=(1+e−αx)22αe−αx=α21−h(x)2
#####两种函数的图像的比较
可拖动滑动条改变 α \alpha α的值来观察图像的变化。
###By the way
神经网络的初始权值和阈值需要归一化0到1之间。
因为神经元的传输函数在[0,1]之间区别比较大,如果大于1以后,传输函数值变化不大(导数或斜率就比较小),不利于反向传播算法的执行。反向传播算法需要用到各个神经元传输函数的梯度信息,当神经元的输入太大时(大于1比如),相应的该点自变量梯度值就过小,就无法顺利实现权值和阈值的调整)。
传输函数比如sigmoid或logsig或tansig,你可以把函数图像画出来,会发现,[-1,1]之间函数图像比较徒,一阶导数(梯度)比较大,如果在这个范围之外,图像就比较平坦,一阶导数(梯度)就接近0了。
#感知器模型
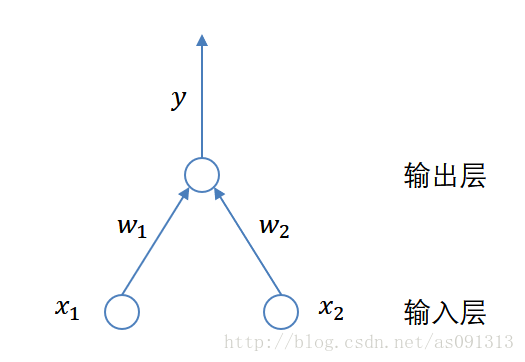
感知器模型,是一种最简单的神经网络模型结构,其网络结构包括输入层与输出层两层,如下图所示:
其为具有两个输入神经元,一个输出神经元的感知器模型。
我们知道该模型是可以做与或非运算的。
这是因为如果我们要做与或非运算,那么对于输入 x 1 , x 2 x1,x2 x1,x2来说,其取值只能是0或1,而我们的输出 y = f ( ∑ i = 1 2 w i x i − θ ) y=f(\sum\limits^{2}_{i=1}w_ix_i−θ) y=f(i=1∑2wixi−θ)。
如果要做与运算,那令阈值 w 1 = 1 , w 2 = 1 , θ = 2 w_1=1,w_2=1,θ=2 w1=1,w2=1,θ=2,则只有在 x 1 = 1 , x 2 = 1 x_1=1,x_2=1 x1=1,x2=1的时候才能激活输出层神经元,输出1,其余情况均输出0。
同样,如果做或运算,那令阈值 w 1 = 1 , w 2 = 1 , θ = 1 w_1=1,w_2=1,θ=1 w1=1,w2=1,θ=1,则只要有一个输入 x i = 1 x_i=1 xi=1,即可激活输出神经元,输出1。
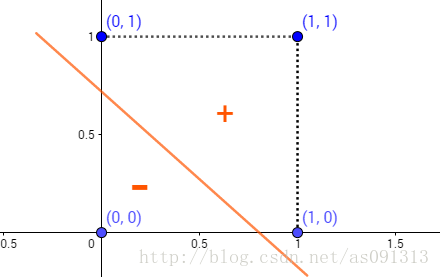
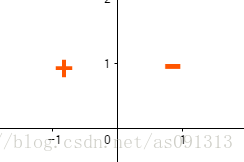
如果对x1做非运算,那么可以令阈值 w 1 = − 0.6 , w 2 = 0 , θ = − 0.5 w_1=−0.6,w_2=0,θ=−0.5 w1=−0.6,w2=0,θ=−0.5,则如果 x 1 = 1 , x 2 = 0 x_1=1,x_2=0 x1=1,x2=0,总输入为−0.6,小于阈值,输出0,如果 x 1 = 0 , x 2 = 0 x_1=0,x_2=0 x1=0,x2=0,总输入为0,大于阈值,输出1。这里的激活函数为阶跃函数。这个通过下面的三幅图也可以看得出来:
与
或
非
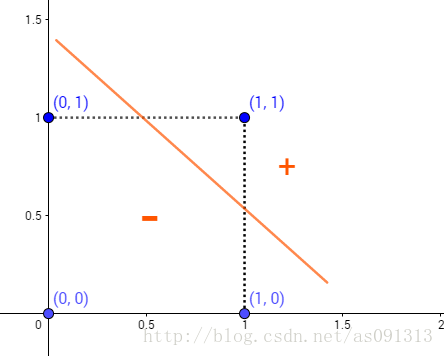
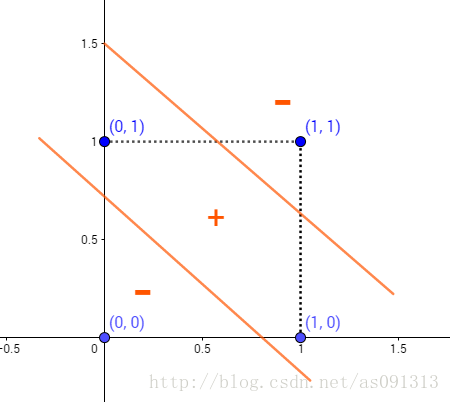
经过观察,可以发现,对于只有输入层与输出层的感知机模型, ∑ i = 1 2 ω i x i − θ \sum\limits^2_{i=1}ω_ix_i−θ i=1∑2ωixi−θ是线性的,其只能对线性数据进行划分,对于如下图的异或模型,其实无法准确划分的。
异或
这可咋办呀。
因为任何一条线都无法将 ( 1 , 0 ) , ( 0 , 1 ) (1,0),(0,1) (1,0),(0,1)划为一类, ( 0 , 0 ) , ( 1 , 1 ) (0,0),(1,1) (0,0),(1,1)划为一类。
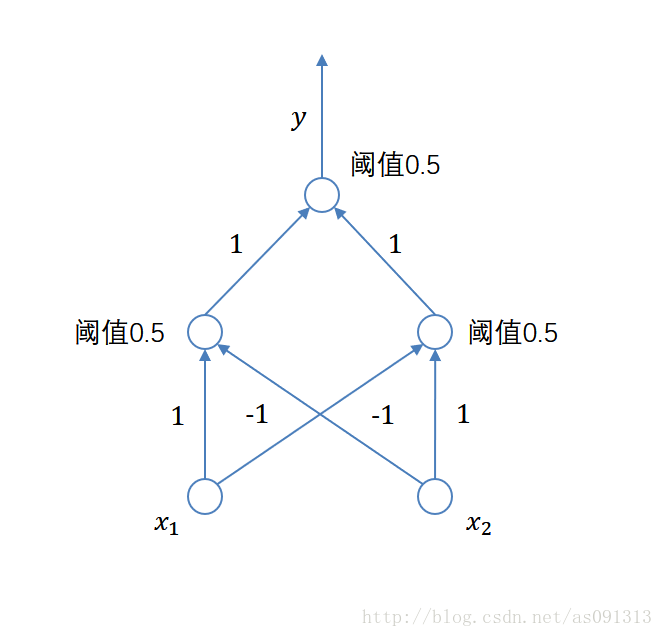
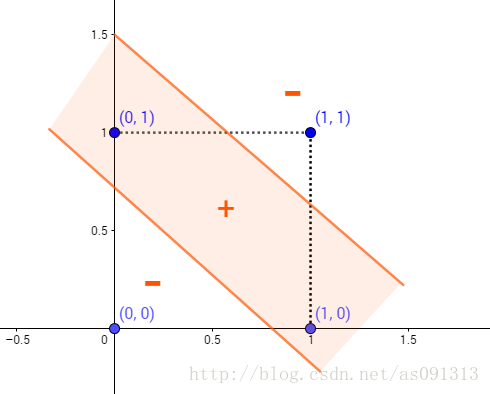
但如果是两层网络(这里的两层指的是隐层与输出层,因为只有这两层中的节点是有激活函数的),在隐层有两个节点,那么此时就可以得到两条线性函数,再在输出节点汇总之后,将会得到由两条直线围成的一个面,这时就可以成功的将异或问题解决。
记得之前做过的那道小学生题目吗?一条线把一个多边形分成两个三角形,最后答案是画一条粗如臂膀的线。
因此我们可以看到,随着网络深度的增加,每一层节点个数的增加,都可以加强网络的表达能力,网络的复杂度越高,其表示能力就越强,也就可以表达更复杂的模型。
通过上面你的示例,我们也可以看到,对网络的学习其实主要是对网络中各个节点之间的连接权值和阈值的学习,即寻找最优的连接权值和阈值从而使得该模型可以达到最优(一般是局部最优)。
#多层前馈(BP)神经网络
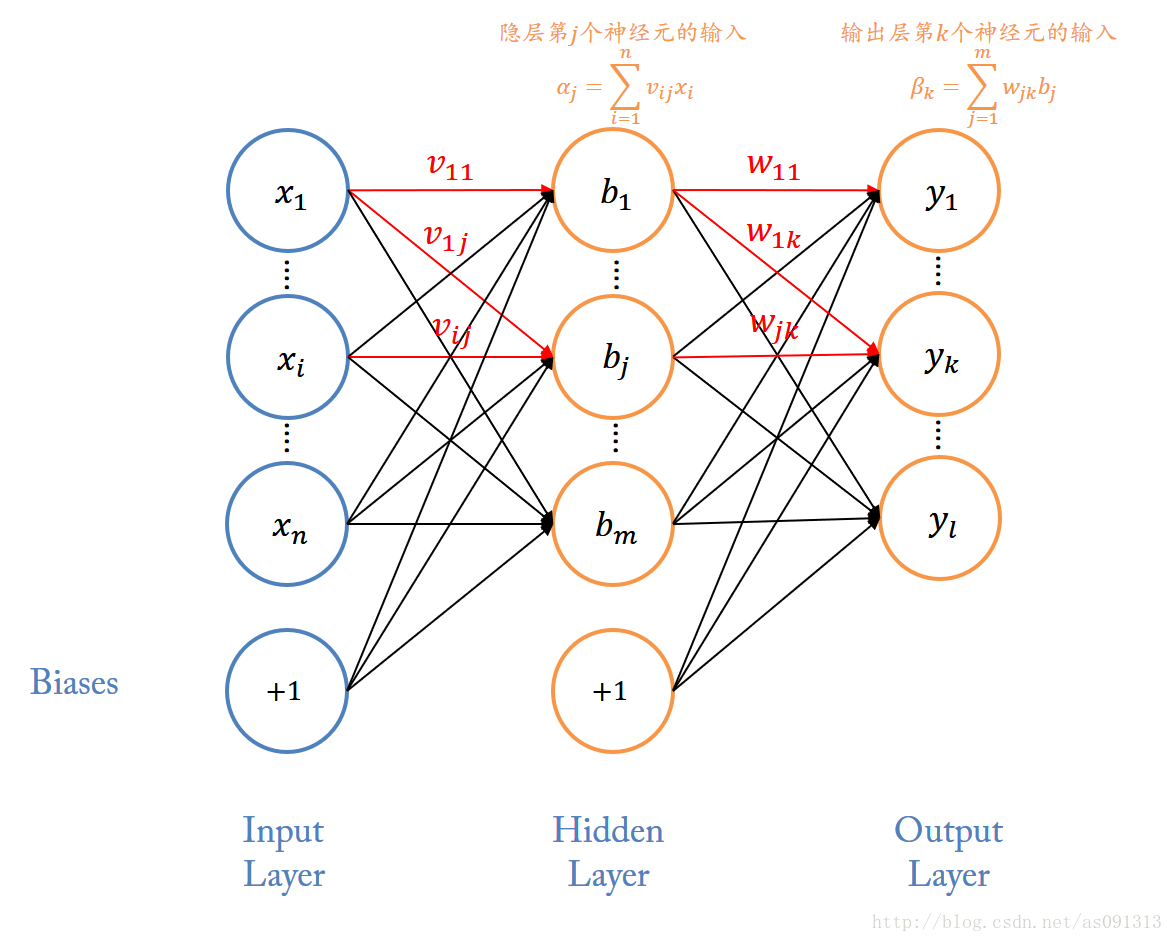
相邻两层是全连接,而层内是没有连接的,跨层之间也没有连接:
在给定训练数据集的情况下,可以构建一个神经网络来对这些数据进行拟合。
构建过程主要分为2步:1)前向传播 2)反向求导。
在前向传播过程中,给定权值和bias矩阵,可以得到给定样本对应的预测值(激活值);在反向求导过程,通过样本预测值与样本真实值之间的误差来不断修正网络参数,直至收敛。
##前向传播
由输入层向前传送。
###输入
####隐层: α j = ∑ i = 1 n v i j x i \alpha_j = \sum\limits_{i=1}^{n}v_{ij}x_i αj=i=1∑nvijxi
####输出层: β k = ∑ j = 1 m w j k b j \beta_k = \sum\limits_{j=1}^{m}w_{jk} b_j βk=j=1∑mwjkbj
###输出
θ j b \theta_j^b θjb表示隐层的第 j j j 个神经元的阈值,请举一反三谢谢。
#### f ( x ) = 1 1 + e − x ( x ∈ R ) f(x)=\frac{1}{1+e^{- x}} \space (x \in R) f(x)=1+e−x1 (x∈R)(取 α = 1 \alpha= 1 α=1)
####隐层: b j = f ( α j − θ j b ) = f ( ∑ i = 1 n v i j x i − θ j b ) b_j=f(\alpha_j - \theta_j^b)=f(\sum\limits_{i=1}^{n}v_{ij}x_i-\theta_j^b) bj=f(αj−θjb)=f(i=1∑nvijxi−θjb)
####输出层: y k = f ( β k − θ k y ) = f ( ∑ j = 1 m w j k b j − θ j y ) y_k=f(\beta_k - \theta_k^y)=f(\sum\limits_{j=1}^{m}w_{jk}b_j-\theta_j^y) yk=f(βk−θky)=f(j=1∑mwjkbj−θjy)
##根据误差(error)反向传送
由于前向传播阶段的权值和bias是随机初始化的,因此需要根据网络输出误差不断的对参数进行修正。
这里要用到梯度下降法,不会的自己去百度,高数上学过(倒三角的那个),但我觉得你连这点时间都懒得去用来查:梯度下降(百度百科),给我认真学啊!!!!!
##误差
设 T k T_k Tk 为预计输出,计算与实际输出的均方差。
## E = 1 2 ∑ k ( T k − y k ) 2 E=\frac{1}{2}\sum\limits_k(T_k-y_k)^2 E=21k∑(Tk−yk)2
##梯度
###输出层
## ∇ w j k = ∂ E ∂ w j k = ∂ E ∂ y k ∂ y k ∂ β k ∂ β k ∂ w j k \nabla_{w_{jk}}=\frac{\partial E}{\partial w_{jk}}=\frac{\partial E}{\partial y_k}\frac{\partial y_k}{\partial \beta_{k}}\frac{\partial \beta_{k}}{\partial w_{jk}} ∇wjk=∂wjk∂E=∂yk∂E∂βk∂yk∂wjk∂βk
其中:
## ∂ E ∂ y k = y k − T k \frac{\partial E}{\partial y_k}=y_k-T_k ∂yk∂E=yk−Tk
## ∂ y k ∂ β k = f ′ ( β k − θ k y ) = f ( β k − θ k y ) [ 1 − f ( β k − θ k y ) ] = y k ( 1 − y k ) \frac{\partial y_k}{\partial \beta_{k}}=f'(\beta_k - \theta_k^y)=f(\beta_k - \theta_k^y)[1-f(\beta_k - \theta_k^y)]=y_k(1-y_k) ∂βk∂yk=f′(βk−θky)=f(βk−θky)[1−f(βk−θky)]=yk(1−yk)
## ∂ β k ∂ w j k = b j \frac{\partial \beta_{k}}{\partial w_{jk}}=b_{j} ∂wjk∂βk=bj
## ∴ ∇ w j k = y k ( 1 − y k ) ( y k − T k ) b j \therefore\nabla_{w_{jk}}=y_k(1-y_k)(y_k-T_k)b_j ∴∇wjk=yk(1−yk)(yk−Tk)bj
## ∇ θ k y = ∂ E ∂ θ k y = ∂ E ∂ y k ∂ y k θ k y \nabla_{\theta^y_k}=\frac{\partial E}{\partial \theta^y_k}=\frac{\partial E}{\partial y_k}\frac{\partial y_k}{\theta^y_k} ∇θky=∂θky∂E=∂yk∂Eθky∂yk
其中:
## ∂ y k θ k y = − f ′ ( β k − θ k y ) = − f ( β k − θ k y ) [ 1 − f ( β k − θ k y ) ] = − y k ( 1 − y k ) \frac{\partial y_k}{\theta^y_k}=-f'(\beta_k - \theta_k^y)=-f(\beta_k - \theta_k^y)[1-f(\beta_k - \theta_k^y)]=-y_k(1-y_k) θky∂yk=−f′(βk−θky)=−f(βk−θky)[1−f(βk−θky)]=−yk(1−yk)
## ∴ ∇ θ k y = − y k ( 1 − y k ) ( y k − T k ) \therefore\nabla_{\theta^y_k}=-y_k(1-y_k)(y_k-T_k) ∴∇θky=−yk(1−yk)(yk−Tk)
###隐层
## ∇ v i j = ∂ E ∂ v i j = ∂ E ∂ b j ∂ b j ∂ v i j \nabla_{v_{ij}}=\frac{\partial E}{\partial v_{ij}}=\frac{\partial E}{\partial b_j}\frac{\partial b_j}{\partial v_{ij}} ∇vij=∂vij∂E=∂bj∂E∂vij∂bj
其中:
由上面知:
## E = 1 2 ∑ k ( T k − y k ) 2 E=\frac{1}{2}\sum\limits_k(T_k-y_k)^2 E=21k∑(Tk−yk)2
## = 1 2 ∑ k ( T k − f ( ∑ j = 1 m w j k b j − θ j y ) ) 2 =\frac{1}{2}\sum\limits_k(T_k-f(\sum\limits_{j=1}^{m}w_{jk}b_j-\theta_j^y))^2 =21k∑(Tk−f(j=1∑mwjkbj−θjy))2
## ∴ ∂ E ∂ b j = ∑ k = 1 l y k ( 1 − y k ) ( T k − y k ) w j k \therefore\frac{\partial E}{\partial b_j}=\sum\limits_{k=1}^ly_k(1-y_k)(T_k-y_k)w_{jk} ∴∂bj∂E=k=1∑lyk(1−yk)(Tk−yk)wjk
## ∂ b j ∂ v i j = b j ( 1 − b j ) x i \frac{\partial b_j}{\partial v_{ij}}=b_j(1-b_j)x_i ∂vij∂bj=bj(1−bj)xi
## ∴ ∇ v i j = ∑ k = 1 l y k ( 1 − y k ) ( T k − y k ) w j k b j ( 1 − b j ) x i = ∑ k = 1 l ∇ w j k w j k ( 1 − b j ) x i \therefore\nabla_{v_{ij}}=\sum\limits_{k=1}^{l}y_k(1-y_k)(T_k-y_k)w_{jk}b_j(1-b_j)x_i=\sum\limits_{k=1}^{l}\nabla_{w_{jk}}w_{jk}(1-b_j)x_i ∴∇vij=k=1∑lyk(1−yk)(Tk−yk)wjkbj(1−bj)xi=k=1∑l∇wjkwjk(1−bj)xi
这样就将两层联系了起来。
同理,就算拓展到两层,三层甚至更多层的隐层都适用。
## ∇ θ j b = ∂ E ∂ θ j b = ∂ E ∂ b j ∂ b j θ j b \nabla_{\theta^b_j}=\frac{\partial E}{\partial \theta^b_j}=\frac{\partial E}{\partial b_j}\frac{\partial b_j}{\theta^b_j} ∇θjb=∂θjb∂E=∂bj∂Eθjb∂bj
其中:
## ∂ b j θ j b = − b j ( 1 − b j ) \frac{\partial b_j}{\theta^b_j}=-b_j(1-b_j) θjb∂bj=−bj(1−bj)
## ∴ ∇ θ j b = ∑ k = 1 l − y k ( 1 − y k ) ( T k − y k ) b j ( 1 − b j ) = ∇ θ k y b j ( 1 − b j ) \therefore\nabla_{\theta^b_j}=\sum\limits_{k=1}^{l}-y_k(1-y_k)(T_k-y_k)b_j(1-b_j)=\nabla_{\theta^y_k}b_j(1-b_j) ∴∇θjb=k=1∑l−yk(1−yk)(Tk−yk)bj(1−bj)=∇θkybj(1−bj)
##权重更新
###设置学习速率为 η \eta η (一般在0.01 ~ 1之间取值)。
## Δ w j k = η ∇ w j k \Delta w_{jk}= \eta\nabla_{w_{jk}} Δwjk=η∇wjk
## Δ v i j = η ∇ v i j \Delta v_{ij}=\eta\nabla_{v_{ij}} Δvij=η∇vij
## w j k ′ = w + Δ w j k w'_{jk}=w+\Delta w_{jk} wjk′=w+Δwjk
## v i j ′ = v + Δ v i j v'_{ij}=v+\Delta v_{ij} vij′=v+Δvij
##偏置更新
## Δ θ k y = η ∇ θ k y \Delta\theta^y_k=\eta\nabla_{\theta^y_k} Δθky=η∇θky
## Δ θ j b = η ∇ θ j b \Delta\theta^b_j=\eta\nabla_{\theta^b_j} Δθjb=η∇θjb
## θ k y ′ = θ k y + η ∇ θ k y \theta^{y'}_k=\theta^y_k+\eta\nabla_{\theta^y_k} θky′=θky+η∇θky
## θ j b ′ = θ j b + η ∇ θ j b \theta^{b'}_j=\theta^b_j+\eta\nabla_{\theta^b_j} θjb′=θjb+η∇θjb
训练终止条件
权重的更新低于某个阈值 。
##预测的错误率低于某个阈值 。
达到预设一定的循环次数。
##换句话说,就是直到网络收敛。
#BP的讨论
##网络层次的选择:
对多层网络要确定选用几个隐蔽层。
Heche-Nielsen证明,当各结点具有不同的阈值时,具有一个隐蔽层的网络可以表示其输入的任意函数,但由于该条件很难满足,该结论意义不大。
Cybenko指出,当各结点均采用S型函数时,一个隐蔽层就足以实现任意判决分类问题,两个隐蔽层则足以实现输入向量的任意输出函数。
网络层次的选取依经验和情况而定,通常不宜过多。
##层内结点数的确定:
BP网络中各层结点数的选择对网络的性能影响很大。
对输出结点,它取决于输出的表示方法和要识别(或分类)的输入向量的类别数目。
比如要输出能表示8个不同向量的分类,可以用8个输出结点,一个结点表示一类,也可以采用三个输出结点,用它们的二进制编码表示8个不同的分类。
如果用了编码方式,会减少输出结点的数量,但会增加隐蔽层的附加工作以完成编码功能,甚至有时需增加一个隐蔽层以满足要求。
对输入结点,输入层的结点数通常应等于输入向量的分量数目。
对隐蔽层结点数的选择,Nielson等指出:
除了图像情况,在大多数情况下,可使用4-5个隐蔽层结点对应一个输入结点。
在图像情况下,像素的数目决定了输入结点的数目,此时隐蔽层结点可取输入结点数的10%左右。
隐蔽层的结点数取得太少,网络将不能建立复杂的判决界面;取得太多,会使得判决界面仅包封了训练点而失去了概括推断的能力。
隐蔽层结点数的选择要根据实际情况和经验来定。
##BP训练算法存在的问题
尽管BP训练算法应用得很广泛,但其训练过程存在不确定性。
###完全不能训练
网络的麻痹现象
局部最小
###训练时间过长,尤其对复杂问题需要很长时间训练。
选取了不适当的调节阶距(训练速率系数 η \eta η)。
###网络的麻痹现象
在训练过程中(如采用Sigmoid函数),加权调得较大可能迫使所有的或大部分的加权和输出sj较大,从而使得操作会在S型函数的饱和区进行,此时函数处在其导数F’(s)非常小的区域内。
由于在计算加权修正量时, Δ w \Delta w Δw正比于 f ′ ( ) f'() f′(),因此当 f ′ ( ) → 0 f'()\rightarrow0 f′()→0时 Δ w → 0 \Delta w\rightarrow0 Δw→0,这使得,相当于调节过程几乎停顿下来。
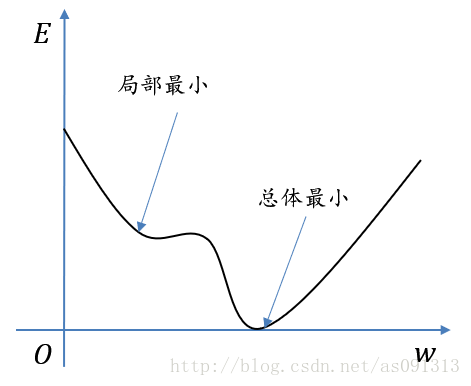
###局部最小
BP训练算法实际上采用梯度下降法,训练过程从某一起始点沿误差函数的斜面最陡方向逐渐达到最小点 E → 0 。 E\rightarrow0。 E→0。
对于复杂的网络,其误差函数面在多维空间,其表面可能凹凸不平,因而在训练过程中可能会陷入某一个小谷区,称之为局部最小点。
由此点向各方向变化均使E增加,以致无法逃出这个局部最小点。
初始随机加权的大小对局部最小的影响很大。如果这些加权太大,可能一开始就使网络处于S型函数的饱和区,系统就很有可能陷入局部最小。
一般来说,要避免局部最小点可采用统计训练的方法。
###随机神经网络
阶距(训练速率系数 η \eta η)大小
如果 η \eta η选得太小,收敛会很慢;
如果 η \eta η选得太大,可能出现连续不稳定现象。
需按照实验和经验确定η。
可取 η \eta η值为0.01~1。
关于BO网络的讨论摘自:BP神经网络解析,稍作修改。
#代码
先略过。
以后再补。
#参考文章
如何简单形象又有趣地讲解神经网络是什么?
ConvnetJS demo: toy 2d classification with 2-layer neural network
神经网络的初始权值和阈值为什么都归一化0到1之间呢
神经网络的结构解析及训练过程概述
神经网络学习笔记
神经网络
BP神经网络解析
特征值和特征向量
如何理解矩阵特征值?
有没有人能用人类的语言告诉我,相似矩阵有什么用?
梯度下降
建议将这些都看一遍,博采众家之长,有助于学习与理解,别想着偷懒,偷懒是没有好下场的。

AtomGit 是由开放原子开源基金会联合 CSDN 等生态伙伴共同推出的新一代开源与人工智能协作平台。平台坚持“开放、中立、公益”的理念,把代码托管、模型共享、数据集托管、智能体开发体验和算力服务整合在一起,为开发者提供从开发、训练到部署的一站式体验。
更多推荐
 已为社区贡献1条内容
已为社区贡献1条内容








所有评论(0)