图的连通分量
目录
CodeForces 762F Simple Cycles Edges
一,无向连通图
1,无向连通图
一个无向图,如果任何两个节点之间都是连通的,则称为无向连通图。
2,割点、割边
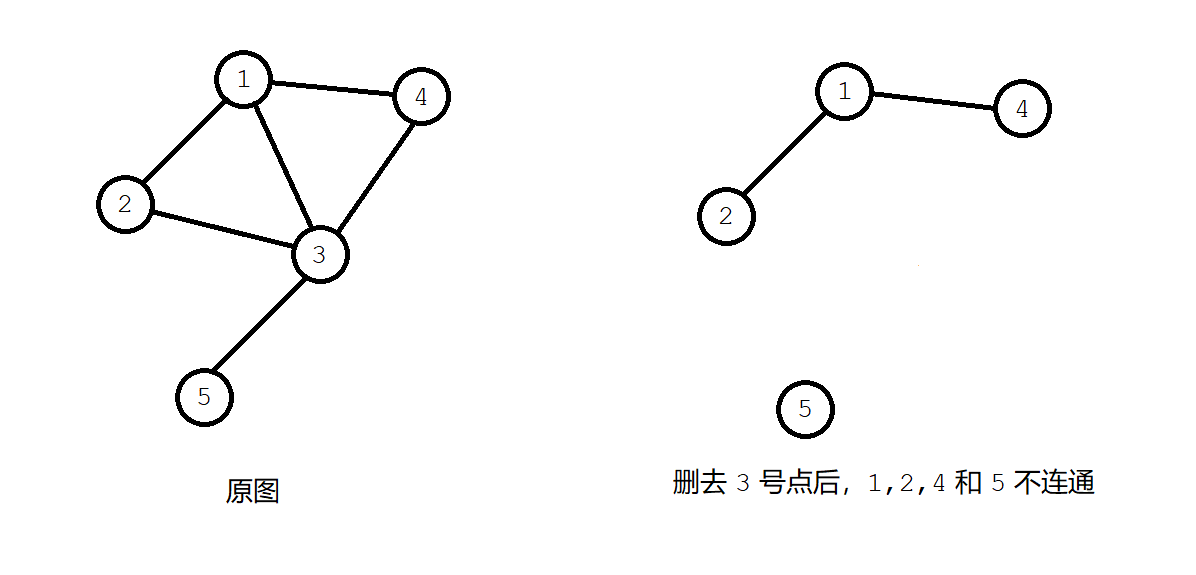
如果一个连通图删掉一个点之后就不再连通,我们称这个点为割点,也叫衔接点。
如果一个连通图删掉一个边之后就不再连通,我们称这个边为割边,也叫桥。


割边不一定是两个割点连接而成,比如一个点是度为1的边缘点。
两个割点连接而成也不一定是割边,比如2个割点之间有2条边。
3,双连通图
如果一个无向图没有割点,则称这个图为点双连通图。
如果一个无向图没有割边,则称这个图为边双连通图。
二,有向连通图
1,强连通图
一个有向图,如果任何两个节点AB之间,从A到B可达,从B到A也可达,则称为强连通图。
一个含有n(n>1)个节点的强连通图,一定可以选出n条边,把n个节点连成一个环(可能自交)。
2,半连通图
一个有向图,如果任何两个节点AB之间,要么从A到B可达要么从B到A可达,则称为半连通图。
半连通图有0个或1个入度为0的节点,有0个入度为0的节点则是有环图,有1个入度为0的节点可能有环可能无环。
半连通图中一定存在一个强连通分量,其中任一节点A到图中其他所有节点都可达。我们把这样的点叫做半连通图的起点。
3,基图
有向图的有向边全变成无向边,得到的无向图称为有向图的基图。
4,弱连通图
如果一个有向图的基图是无向连通图,则称该有向图为弱连通图。
弱连通图不是半连通图的例子:

5,线状图
线状图的n个节点,可以用编号1,2,3,...,n来表示,图中存在一条1->2->3->...->n的路径,除此之外还存在若干i->j(i<j)的路径,不存在x->y(x>y)的路径,那么这个图叫线状图。
线状图中任意两点之间的连通性、最短路径等信息,都由1->2->3->...->n的路径来给出,所以说这条路径就是这个图的核心。
PS:一个有向图是线状图,等价于这个有向图有唯一的拓扑排序。
6,收缩生成图
把一个半连通图进行收缩,每个强连通分量Gi变成一个点Ai,Ai到Aj是否连一条边,取决于是否存在一条边从Gi中的点到Gj中的点,如此收缩操作,生成的一定是一个线状图。
PS:收缩生成图是一种广义子图。
三,连通分量
1,连通分量
一个图的极大连通子图,称为连通分量。连通图有若干种,连通分量也就对应的有若干种。
PS:连通图的定义,都会保证“极大连通子图”这个概念是自洽的。
2,连通分量分割
连通分量分割指的是从一个图A找出一个连通分量,从A中删掉这个子图,剩下的图继续分割,直到A变成空图,这样就把A分成若干个连通分量。
性质:
(1)A的每个点都属于某个连通分量,但可能会有一些边不在任意一个连通分量中。
(2)不同分量之间的节点没有重复的。
(3)无向连通分量分割、双连通分量分割、强连通分量分割、弱连通分量分割的结果都是唯一的,且每个连通分量都是原图的连通分量。
(4)半连通分量分割的不是唯一的,取决于分割顺序,且除了第一个连通分量,其他连通分量都是中间图的连通分量,可能不是原图的连通分量,只能说是原图的连通子图。
无论如何分割,原图的任意一个强连通分量一定是某个半连通分量的子图,而不会被割裂。

比如这个图,有这几种不同的分割结果:




3,无向连通分量分割
一般都用并查集来计算,在这篇博客中有很多求无向连通分量的OJ题目。
4,双连通分量分割
边双连通分量不含割边,换句话说就是把无向图的割边都删掉之后,剩下的图的所有无向连通分量就是原图的所有边双连通分量。
非割点只属于一个点双连通分量,割点属于一个到多个点双连通分量。
5,弱连通分量分割
即基图的无向连通分量分割。
6,半连通子图分割
我们把一个图分割成若干个连通子图,只要求强连通分量不被割裂,不要求连通子图是极大连通子图。
用DFS算法即可。
(1)在A中任选一节点作为DFS的起点
(2)进行DFS,完成搜索之后,所有经过的点和他们在A中的边就构成一个半连通分量
(3)从A中删掉这个子图,剩下的图回到(1)继续处理,直到A是空图。
PS:这样得到的半连通分量,都是带起点的。
//DFS从k开始遍历,记录所有节点最后一次访问的顺序的反序
void DFS(map<int, vector<int>>& m, map<int, int>& visit, int k, vector<int>& ans)
{
if (visit[k])return;
visit[k] = 1;
for (auto i : m[k])DFS(m, visit, i, ans);
ans.insert(ans.begin(), k);
}
//半连通分量分割
vector<vector<int>> SemiConnectComponent(map<int, vector<int>>& m)
{
vector<vector<int>>allans;
map<int, int>visit;
for (auto& mi : m) {
int k = mi.first;
if (visit[k])continue;
vector<int>ans;
DFS(m, visit, k, ans);
allans.push_back(ans);
}
return allans;
}7,强连通分量分割
在进行半连通子图分割的基础上,后面我们只需要考虑如何对一个带起点的半连通图进行强连通分量分割即可。
(1)DFS遍历整个半连通图A,得到所有节点离开的顺序列表L的反序列表L2
(2)按照L2,依次作为DFS的起点对A的反向图进行DFS
(3)每次DFS经过的所有节点构成一个强连通分量,在L2中删掉这些节点。
这其实就是Kosaraju算法的思路。
PS:这里的第(1)步和半连通子图分割是重合的过程,并不是先做完半连通子图分割之后才做第(1)步。
四,Kosaraju算法
以力扣802的图为例:

首先得到半连通分量
size = 3
size = 5: 0 1 3 2 5
size = 1: 4
size = 1: 6
再求解强连通分量:
size = 5
size = 3:0 3 1
size = 1:2
size = 1:5
size = 1:4
size = 1:6
//根据邻接表构建有向图的反向图
map<int, vector<int>> Reverse(const map<int, vector<int>>& m)
{
map<int, vector<int>> ans;
for (auto& mi : m) {
for (auto& k : mi.second)ans[k].push_back(mi.first);
}
return ans;
}
//取子图
map<int, vector<int>> GetSubG(map<int, vector<int>>& m, vector<int>& v)
{
map<int, vector<int>>ans;
map<int, int>mv;
for (auto vi : v)mv[vi] = 1;
for (auto vi : v) {
for (auto mi : m[vi]) {
if (mv[mi])ans[vi].push_back(mi);
}
}
return ans;
}
//强连通分量分割
vector<vector<int>> ConnectComponent(map<int, vector<int>>& m)
{
vector<vector<int>> semi = SemiConnectComponent(m);
auto m2 = Reverse(m);
vector<vector<int>>allans;
map<int, int>visit;
for (auto& s : semi) {
auto m3 = GetSubG(m2, s);
for (auto& k : s) {
if (visit[k])continue;
vector<int>ans;
DFS(m3, visit, k, ans);
allans.push_back(ans);
}
}
return allans;
}力扣 802. 找到最终的安全状态
有一个有 n 个节点的有向图,节点按 0 到 n - 1 编号。图由一个 索引从 0 开始 的 2D 整数数组 graph表示, graph[i]是与节点 i 相邻的节点的整数数组,这意味着从节点 i 到 graph[i]中的每个节点都有一条边。
如果一个节点没有连出的有向边,则它是 终端节点 。如果没有出边,则节点为终端节点。如果从该节点开始的所有可能路径都通向 终端节点 ,则该节点为 安全节点 。
返回一个由图中所有 安全节点 组成的数组作为答案。答案数组中的元素应当按 升序 排列。
示例 1:

输入:graph = [[1,2],[2,3],[5],[0],[5],[],[]] 输出:[2,4,5,6] 解释:示意图如上。 节点 5 和节点 6 是终端节点,因为它们都没有出边。 从节点 2、4、5 和 6 开始的所有路径都指向节点 5 或 6 。
示例 2:
输入:graph = [[1,2,3,4],[1,2],[3,4],[0,4],[]] 输出:[4] 解释: 只有节点 4 是终端节点,从节点 4 开始的所有路径都通向节点 4 。
提示:
n == graph.length1 <= n <= 1040 <= graph[i].length <= n0 <= graph[i][j] <= n - 1graph[i]按严格递增顺序排列。- 图中可能包含自环。
- 图中边的数目在范围
[1, 4 * 104]内。
思路:首先求取强连通分量,然后把非孤立点的强连通分量和有自环的孤立点全部找出来,能到达这些点的都是不安全节点,其他的就是安全节点。
class Solution {
public:
vector<int> eventualSafeNodes(vector<vector<int>>& graph) {
map<int, vector<int>>m;
for (int i = 0; i < graph.size(); i++)m[i] = graph[i];
vector<vector<int>> cc = ConnectComponent(m);
vector<int> notSafe;
for (auto& c : cc) {
if (c.size() > 1)for (auto& k : c)notSafe.push_back(k);
else if (find(m[c[0]].begin(), m[c[0]].end(), c[0]) != m[c[0]].end())notSafe.push_back(c[0]);
}
auto m2 = Reverse(m);
map<int, int>visit;
for (auto& k : notSafe) {
if (visit[k])continue;
vector<int>ans;
DFS(m2, visit, k, ans);
}
vector<int>safe;
for (int i = 0; i < graph.size(); i++)if (visit[i] == 0)safe.push_back(i);
return safe;
}
};PS:其中调用的自定义函数的源码都在本文中。
五,Tarjan算法
1,割点、割边、点连通分量
进行一次DFS搜完整个图,记录dfn和low2个数组,即可得到割边和割点。
其中dfn是每个节点的首次visit时间,low是一个节点和它所有子节点中,只通过一条后向边能走到的最小dfn节点的dfn值。
这里的子节点和后向边,都是和这次DFS得到的深度优先树相对应。
(1)割点
对于根节点k,如果子树数量是1则不是割点,数量大于1则是割点。
对于非根节点k和它的子节点nk,如果low[nk] < dfn[k],则k不是割点,如果对于每个子节点都不满足上式,则k是割点。
(2)割边
对于节点k和它的子节点nk,如果low[nk] >= dfn[nk],则n到nk之间的边是割边,否则就不是割边。
(3)点连通分量
对于叶子节点nk,nk单独成一个点连通分量。
对于节点k和它的子节点nk,如果low[nk] >= dfn[k],则nk所在的子树(加上k)就是一个点连通分量。
有一些场景需要特判,为了核心函数的简洁,我提取了FillConv作为补充流程。
conv和convb分别记录点连通分量的点集和边集,边用a*n+b转化成整数表示。
class TarjanDoubledirect
{
public:
vector<pair<int, int>>cutb;//割边
vector<int>cutv;//割点
vector<vector<int>>conv;//点双连通分量的点集
vector<vector<long long>>convb;//点双连通分量的边集
int cons = 0;//无向连通分量数目
TarjanDoubledirect(int n, map<int, vector<int>>& m)
{
this->n = n;
this->m = m;
visit.resize(n);
added.resize(n);
dfn.resize(n);
low.resize(n);
for (int i = 0; i < n; i++)if (!visit[i]) {
root = i;
dfs(i);
cons++;
}
FillConv();
}
private:
void dfs(int k)
{
visit[k] = true;
low[k] = dfn[k] = dfnId++;
bool cv = false;
int chNum = 0;
st.push(k);
for (auto nk : m[k]) {
if (isBackB(nk))low[k] = min(low[k], dfn[nk]);
if (visit[nk])continue;
chNum++;
sFa.push(k);
dfs(nk);
sFa.pop();
low[k] = min(low[k], low[nk]);
vector<int>conv1;
vector<long long>convb1;
if (low[nk] >= dfn[k]) {
cv = true;
for (int time = INT_MAX; time; time--) {
if (st.top() == nk)time = 1;
conv1.push_back(st.top());
added[st.top()] = true;
for (auto i : m[st.top()])if (!added[i])convb1.push_back((long long)(st.top()) * n + i);
st.pop();
}
if (conv1.size() > 1) {
conv1.push_back(k);
conv.push_back(conv1);
convb.push_back(convb1);
}
}
if (low[nk] >= dfn[nk])cutb.push_back(make_pair(k, nk));
}
if ((k != root && cv && chNum > 0) || (k == root && chNum > 1))cutv.push_back(k);
}
bool isBackB(int nk) // 判断从k到nk是不是后向边
{
return visit[nk] && (sFa.empty() || nk != sFa.top());//如果st.top()是nk,则是树边,不是后向边
}
void FillConv()//补充由单点组成的点连通分量
{
map<int, int>m;
for (auto& ci : conv) {
for (auto& k : ci)m[k] = 1;
}
vector<int>conv1(1);
for (int i = 0; i < n; i++)if (m[i] == 0) {
conv1[0] = i;
conv.push_back(conv1);
convb.push_back(vector<long long>());
}
}
int n;
int dfnId = 0;
int root;
vector<bool>visit;//DFS访问标记
vector<bool>added;
vector<int>dfn;//首次访问的次序
vector<int>low;//通过一条后向边能达到的最小dfn
map<int, vector<int>> m;//邻接表
stack<int>sFa;//用于判断父节点
stack<int>st;
};力扣 1192. 查找集群内的关键连接
力扣数据中心有 n 台服务器,分别按从 0 到 n-1 的方式进行了编号。它们之间以 服务器到服务器 的形式相互连接组成了一个内部集群,连接是无向的。用 connections 表示集群网络,connections[i] = [a, b] 表示服务器 a 和 b 之间形成连接。任何服务器都可以直接或者间接地通过网络到达任何其他服务器。
关键连接 是在该集群中的重要连接,假如我们将它移除,便会导致某些服务器无法访问其他服务器。
请你以任意顺序返回该集群内的所有 关键连接 。
示例 1:

输入:n = 4, connections = [[0,1],[1,2],[2,0],[1,3]] 输出:[[1,3]] 解释:[[3,1]] 也是正确的。
示例 2:
输入:n = 2, connections = [[0,1]] 输出:[[0,1]]
提示:
2 <= n <= 105n - 1 <= connections.length <= 1050 <= ai, bi <= n - 1ai != bi- 不存在重复的连接
题意:
求所有割边。
class Solution {
public:
vector<vector<int>> criticalConnections(int n, vector<vector<int>>& connections) {
map<int, vector<int>>m = undirectedEdgeToAdjaList(connections);
vector<pair<int, int>> cutb = Tarjan (n, m).cutb;
vector<vector<int>>ans;
for (auto &ci : cutb)ans.push_back(vector<int>{ ci.first,ci.second });
return ans;
}
//输入无向边集{{1,2}{1,3}{2,3}},输出邻接表{1:{2,3},2:{1,3},3:{1,2}}
map<int, vector<int>> undirectedEdgeToAdjaList(vector<vector<int>>& v)
{
map<int, vector<int>> ans;
for (auto &vi : v) {
ans[vi[0]].push_back(vi[1]);
ans[vi[1]].push_back(vi[0]);
}
return ans;
}
};
力扣 LCP 54. 夺回据点
欢迎各位勇者来到力扣城,本次试炼主题为「夺回据点」。
魔物了占领若干据点,这些据点被若干条道路相连接,roads[i] = [x, y] 表示编号 x、y 的两个据点通过一条道路连接。
现在勇者要将按照以下原则将这些据点逐一夺回:
-
在开始的时候,勇者可以花费资源先夺回一些据点,初始夺回第
j个据点所需消耗的资源数量为cost[j] -
接下来,勇者在不消耗资源情况下,每次可以夺回一个和「已夺回据点」相连接的魔物据点,并对其进行夺回
注:为了防止魔物暴动,勇者在每一次夺回据点后(包括花费资源夺回据点后),需要保证剩余的所有魔物据点之间是相连通的(不经过「已夺回据点」)。
请返回勇者夺回所有据点需要消耗的最少资源数量。
注意:
- 输入保证初始所有据点都是连通的,且不存在重边和自环
示例 1:
输入:
cost = [1,2,3,4,5,6]roads = [[0,1],[0,2],[1,3],[2,3],[1,2],[2,4],[2,5]]输出:
6解释: 勇者消耗资源
6夺回据点0和4,魔物据点1、2、3、5相连通; 第一次夺回据点1,魔物据点2、3、5相连通; 第二次夺回据点3,魔物据点2、5相连通; 第三次夺回据点2,剩余魔物据点5; 第四次夺回据点5,无剩余魔物据点; 因此最少需要消耗资源为6,可占领所有据点。
示例 2:
输入:
cost = [3,2,1,4]roads = [[0,2],[2,3],[3,1]]输出:
2解释: 勇者消耗资源
2夺回据点1,魔物据点0、2、3相连通; 第一次夺回据点3,魔物据点2、0相连通; 第二次夺回据点2,剩余魔物据点0; 第三次夺回据点0,无剩余魔物据点; 因此最少需要消耗资源为2,可占领所有据点。
提示:
1 <= roads.length, cost.length <= 10^50 <= roads[i][0], roads[i][1] < cost.length1 <= cost[i] <= 10^9
思路:
先按照点连通分量缩点,再找出其中所有只含0-1个原图割点的那些分量,每个分量选一个cost,把最大的cost去掉剩下的加起来就是答案。
class Solution {
public:
long long minimumCost(vector<int>& cost, vector<vector<int>>& roads) {
map<int, vector<int>>m = undirectedEdgeToAdjaList(roads);
auto g = TarjanDoubledirect(cost.size(), m);
vector<int>cutv = g.cutv;//割点
vector<vector<int>>conv = g.conv;//点双连通分量
map<int, int>cutvm;
for (auto ci : cutv)cutvm[ci] = 1;
long long ans = 0;
int themax = INT_MIN;
for (auto& ci : conv) {
int m = INT_MAX;
int num = 0;
for (auto k : ci) {
if (cutvm[k] == 0)m = min(m, cost[k]);
else num++;
}
if (m == INT_MAX)m = 0;
if (num <= 1) {
ans += m;
themax = max(themax, m);
}
}
return ans - (conv.size() > 1 ? themax : 0);
}
//输入无向边集{{1,2}{1,3}{2,3}},输出邻接表{1:{2,3},2:{1,3},3:{1,2}}
map<int, vector<int>> undirectedEdgeToAdjaList(vector<vector<int>>& v)
{
map<int, vector<int>> ans;
for (auto& vi : v) {
ans[vi[0]].push_back(vi[1]);
ans[vi[1]].push_back(vi[0]);
}
return ans;
}
};CodeForces 762F Simple Cycles Edges
https://codeforces.com/contest/962/problem/F
You are given an undirected graph, consisting of nn vertices and mm edges. The graph does not necessarily connected. Guaranteed, that the graph does not contain multiple edges (more than one edges between a pair of vertices) or loops (edges from a vertex to itself).
A cycle in a graph is called a simple, if it contains each own vertex exactly once. So simple cycle doesn't allow to visit a vertex more than once in a cycle.
Determine the edges, which belong to exactly on one simple cycle.
Input
The first line contain two integers nn and mm (1≤n≤100000(1≤n≤100000, 0≤m≤min(n⋅(n−1)/2,100000))0≤m≤min(n⋅(n−1)/2,100000)) — the number of vertices and the number of edges.
Each of the following mm lines contain two integers uu and vv (1≤u,v≤n1≤u,v≤n, u≠vu≠v) — the description of the edges.
Output
In the first line print the number of edges, which belong to exactly one simple cycle.
In the second line print the indices of edges, which belong to exactly one simple cycle, in increasing order. The edges are numbered from one in the same order as they are given in the input.
Examples
input
3 3 1 2 2 3 3 1
output
3 1 2 3
input
6 7 2 3 3 4 4 2 1 2 1 5 5 6 6 1
output
6 1 2 3 5 6 7
input
5 6 1 2 2 3 2 4 4 3 2 5 5 3
output
0
思路:
求出所有点连通分量,校验每个点连通分量是不是简单环即可。
思路一:
根据用点连通分量的点集,把点连通分量的所有边求出来。
int GetSubG(map<int, vector<int>>& m, vector<int>& v, map<int, vector<int>>&ans)
{
int num = 0;
map<int, int>mv;
for (auto vi : v)mv[vi] = 1;
for (auto vi : v) {
ans[vi].reserve(m[vi].size());
for (auto k : m[vi]) {
if (mv[k]) {
ans[vi].push_back(k);
num++;
}
}
}
return num / 2;
}超时,因为多次运行GetSubG的整体时间复杂度是平方级的。
乍一看时间复杂度是线性的,然而割点可能会出现在多个点连通分量中,如果这个割点还有非常高的度的话,那么整体时间复杂度就是平方级的。
思路二,在Tarjan中直接输出点连通分量的边集(为了做这题,把Tarjan代码刷新了,新增了输出点连通分量的边集的功能)。
#include <iostream>
#include <vector>
#include <map>
#include <iomanip>
#include <string>
#include <algorithm>
#include <cmath>
#include <stack>
#include <set>
#include <unordered_map>
#include <queue>
using namespace std;
class Tarjan
{
省略
};
int main()
{
ios::sync_with_stdio(false);
int n, n2;
map<int, vector<int>>m;
cin >> n >> n2;
vector<pair<int, int>>v(n2);
for (int i = 0;i < n2;i++) {
cin >> v[i].first>>v[i].second;
m[--v[i].first].push_back(--v[i].second);
m[v[i].second].push_back(v[i].first);
}
auto g = Tarjan(n, m);
vector<vector<int>>conv = g.conv;//点双连通分量
vector<vector<long long>>convb = g.convb;
map<int, int>ans;
for (int i = 0; i < conv.size();i++) {
if (conv[i].size() == convb[i].size()) {
for (auto& b : convb[i])ans[b] = 1;
}
}
int num = ans.size();
cout << num <<endl;
for (int i = 0; i < v.size(); i++)if ((long long)ans[v[i].first * n + v[i].second] || (long long)ans[v[i].second * n + v[i].first]) {
cout << i + 1;
num--;
if (num)cout << " ";
}
return 0;
}2,强连通分量
和无向图的点连通分量差不多,也是用dfn和low即可求出强连通分量
class TarjanStrongConnect
{
public:
vector<vector<int>>conv;//强连通分量的点集
TarjanStrongConnect(int n, map<int, vector<int>>& m)
{
this->n = n;
this->m = m;
visit.resize(n);
added.resize(n);
dfn.resize(n);
low.resize(n);
for (int i = 0; i < n; i++)if (!visit[i]) {
root = i;
dfs(i);
}
FillConv();
}
private:
void dfs(int k)
{
visit[k] = true;
low[k] = dfn[k] = dfnId++;
bool cv = false;
int chNum = 0;
st.push(k);
for (auto nk : m[k]) {
if (isBackB(nk))low[k] = min(low[k], dfn[nk]);
if (visit[nk])continue;
chNum++;
dfs(nk);
low[k] = min(low[k], low[nk]);
}
vector<int>conv1;
vector<long long>convb1;
if (low[k] >= dfn[k]) {
cv = true;
for (int time = INT_MAX; time; time--) {
if (st.top() == k)time = 1;
conv1.push_back(st.top());
added[st.top()] = true;
st.pop();
}
conv.push_back(conv1);
}
}
bool isBackB(int nk) // 判断从k到nk是不是后向边
{
return visit[nk] && !added[nk];
}
void FillConv()//补充由单点组成的点连通分量
{
map<int, int>m;
for (auto& ci : conv) {
for (auto& k : ci)m[k] = 1;
}
vector<int>conv1(1);
for (int i = 0; i < n; i++)if (m[i] == 0) {
conv1[0] = i;
conv.push_back(conv1);
}
}
int n;
int dfnId = 0;
int root;
vector<bool>visit;//DFS访问标记
vector<bool>added;
vector<int>dfn;//首次访问的次序
vector<int>low;//通过一条后向边能达到的最小dfn
map<int, vector<int>> m;//邻接表
stack<int>st;
};力扣 802. 找到最终的安全状态
只把求强连通分量的一行改掉即可。
class Solution {
public:
vector<int> eventualSafeNodes(vector<vector<int>>& graph) {
map<int, vector<int>>m;
for (int i = 0; i < graph.size(); i++)m[i] = graph[i];
vector<vector<int>> cc = Tarjan(graph.size(),m).conv;//只改一行
vector<int> notSafe;
for (auto& c : cc) {
if (c.size() > 1)for (auto& k : c)notSafe.push_back(k);
else if (find(m[c[0]].begin(), m[c[0]].end(), c[0]) != m[c[0]].end())notSafe.push_back(c[0]);
}
auto m2 = Reverse(m);
map<int, int>visit;
for (auto& k : notSafe) {
if (visit[k])continue;
vector<int>ans;
DFS(m2, visit, k, ans);
}
vector<int>safe;
for (int i = 0; i < graph.size(); i++)if (visit[i] == 0)safe.push_back(i);
return safe;
}
};更多推荐
 已为社区贡献3条内容
已为社区贡献3条内容









所有评论(0)